Lattice quivers #
Recap #
In Path quivers we saw how to construct the forward path quiver \( \forwardPathQuiver{\quiver{F}}{\vert{x}} \) from a quiver \( \quiver{F} \), and in Path quotients we saw how to define the path quotient quiver \( \quotient{\forwardPathQuiver{\quiver{F}}{\vert{x}}}{\pathMap{ \mu }} \) with respect some path valuation \( \functionSignature{\groupoidHomomorphism{ \mu }}{\pathGroupoid{\quiver{F}}}{\group{V}} \), which maps paths to "path values" in some group \( \group{V} \). We examined the particularly simple case of affine path valuations \( \affineModifier{\groupoidHomomorphism{ \phi }} \) that are induced by a group homomorphism \( \functionSignature{\groupoidHomomorphism{ \phi }}{\wordGroup{\quiver{F}}}{\group{V}} \), yielding quotients written \( \compactQuotient{\quiver{F}}{\vert{x}}{\groupoidFunction{ \phi }} \). The affine path valuations are path valuations that depend only on the word of a path: \( \function{\affineModifier{\groupoidHomomorphism{ \phi }}}(\path{P}) = \groupoidHomomorphism{ \phi }(\wordOf(\path{P})) \).
We'll now put this construction to work to build lattice quivers, which are quotients of simple fundamental quivers \( \quiver{F} \) by affine path valuations induced by homomorphisms into Abelian groups that capture the translational symmetries of crystallographic lattices. These will give us an alternative way to view the quivers we constructed in Transitive quivers and Cayley quivers.
Representations #
Group representations #
Recall from Cayley quivers that a right group action \( \function{A} \) is a "binding" of a group \( \group{G} \) to an object \( \sym{X} \) on which it acts, expressed as a structure-preserving map \( \functionSignature{\function{\action{A}}}{\TuFo{\sym{X}, \group{G}}}{\sym{X}} \). By fixing the second argument of the two-argument map \( \function{A} \) we obtain a family of functions \( \setConstructor{\functionSignature{\function{\action{A}_{\groupElement{g}}}}{\sym{X}}{\sym{X}}}{\elemOf{\groupElement{g}}{\group{G}}} \), it is these Cayley functions that encode the behavior of the group \( \group{G} \), with function composition playing the role of group multiplication.
Group actions are usually obtained by associating each element of \( \group{G} \) with some form of isomorphism of the object \( \sym{X} \). This can be formalized using a group homomorphism \( \functionSignature{\groupoidFunction{ \pi }}{\group{G}}{\automorphisms(\sym{X})} \), where \( \automorphisms(\sym{X}) \) represents the group of relevant symmetries of the object \( \sym{X} \).
When \( \sym{X} \) is a set, the isomorphisms are permutations of \( \sym{X} \), so that \( \automorphisms(\sym{X}) = \symmetricGroup{\sym{X}} \), and the group actions are known as permutation representations.
When \( \sym{X} \) is a vector space, these group actions are known as linear representations. In that case, \( \automorphisms(\sym{X}) \) is just the space of linear transformations of \( \sym{X} \), and if this space is also finite dimensional, we can represent these linear transformations as square matrices living in a subgroup of \( \generalLinearGroup{n}{\field{K}} \), for some field \( \field{K} \), typically \( \field{\re} \) or \( \field{\mathbb{C}} \). A vast body of theory has been built around studying and classifying such representations with many applications in physics and elsewhere.
To summarize, group representations are models of groups: concrete instantiations of the behavior of the group in the form of transformations of a set or vector space. These instantiations can capture all the behavior, meaning that different group elements are sent to unique transformations, in which case they are called faithful. Or they might lose information; in the case of the trivial representation, every group element is represented as the identity transformation, and we've lost all the information about the original group.
Path representations #
Linear path representations #
Having introduced linear representations of groups, it is obvious to ask how we might build linear representations of the path groupoid of a quiver: we might call these linear path representations.
Clearly a linear path representation would involve a groupoid homomorphism \( \functionSignature{\groupoidHomomorphism{ \mu }}{\pathGroupoid{\quiver{F}}}{\generalLinearGroup{\sym{n}}{\field{K}}} \). But we’ve already encountered a class of such homomorphisms in the form of affine path valuations \( \functionSignature{\function{\affineModifier{\pathHomomorphism{ \phi }}}}{\pathGroupoid{\quiver{F}}}{\group{V}} \) induced by group homomorphisms \( \functionSignature{\groupHomomorphism{ \phi }}{\wordGroup{\quiver{F}}}{\group{V}} \). If we now choose a linear representation \( \functionSignature{\groupHomomorphism{ \pi }}{\group{V}}{\generalLinearGroup{\sym{n}}{\field{k}}} \) of the group \( \group{V} \), we can compose these \( \groupoidHomomorphism{ \mu }\defEqualSymbol \functionComposition{\pathHomomorphism{ \pi }\functionCompositionSymbol \affineModifier{\pathHomomorphism{ \phi }}} \) to obtain a linear path representation \( \functionSignature{\groupoidHomomorphism{ \mu }}{\pathGroupoid{\quiver{F}}}{\generalLinearGroup{\sym{n}}{\field{k}}} \).
Describing linear path representations #
Recall an important property of group homomorphisms \( \functionSignature{\groupHomomorphism{ \phi }}{\wordGroup{\quiver{F}}}{\group{V}} \): they are uniquely determined by their behavior on the cardinals of \( \quiver{Q} \), since these are the generators of word group \( \wordGroup{\quiver{F}} \). This allows us to describe \( \groupHomomorphism{ \phi } \) as an association between cardinals and \( \sym{n}\times \sym{n} \) matrices:
\[ \groupHomomorphism{ \phi } = \homomorphismMapping{\mto{\card{c}_1}{\matrix{M_1}},\elSy,\mto{\card{c}_{\sym{k}}}{\matrix{M_{\sym{k}}}}} \]Quotients vs path representations #
As before, a path representation models paths as elements of \( \generalLinearGroup{\sym{n}}{\field{K}} \), but by taking quotients we will be deliberately discarding information in order to conflate precisely those paths sharing a tail vertex that we wish to lead to the same head vertex. For suitable representations, this conflation will "fold" the tree \( \subSize{\treeQuiver{\sym{k}}}{ \infty } \) produced by the forward path quiver into a finite-dimensional quiver. (In abstract algebra, this kind of construction is ubiquitous, generically referred to as taking a quotient of a freely generated object in order to impose some desired relations).
While we will be focused on simply using path quotients to construct lattice quivers, we will keep the path representation interpretation in mind for the remainder of this section, and the matrix machinery that goes along with group representations will be an useful "universal format" for doing computations.
Computation #
We wish to actually compute the quotient \( \compactQuotient{\quiver{F}}{\vert{x}}{\groupHomomorphism{ \phi }} \), where \( \functionSignature{\groupHomomorphism{ \phi }}{\cardinalList(\quiver{Q})}{\generalLinearGroup{\sym{n}}{\field{K}}} \) is a map assigning a matrix \( \groupHomomorphism{ \phi }(\card{c}) \) to each cardinal \( \elemOf{\card{c}}{\cardinalList(\quiver{F})} \). Of course, the quotient is usually infinite, so we can only generate a finite part of it, which we'll generally call a fragment.
The following describes how we can use a well-worn algorithm from computer science to compute fragments of the lattice quiver, known as a breadth-first graph traversal.
\[ \TuFo{\vert{x}, \matrix{M}} \]First, define a state as representing an equivalence class of paths starting at the base vertex \( \vert{v} \). We'll represent these states with pairs \( \TuFo{\vert{x}, \matrix{M}} \), where \( \vert{x} \) is a vertex of the fundamental quiver representing the head of the path, and \( \matrix{M} \) is the value of the path as represented by a matrix.
We start with a single state \( \TuFo{\vert{x}, \matrix{M}} = \TuFo{\vert{v}, \matrix{I}} \) representing the empty path at the the base vertex \( \vert{v} \), with path matrix \( \matrix{M} \) equal to the identity matrix \( \matrix{I} \). We then extend this empty path by all cardinals \( \card{c}_{\sym{i}} \) corresponding to edges \( \tde{\vert{v}}{\vert{w_i}}{\card{\card{c}_{\sym{i}}}} \) in the fundamental quiver, right-multiplying our current value of \( \matrix{M} \) by the corresponding cardinal matrices \( \groupoidFunction{ \phi }(\card{c}) \) to obtain new states \( \TuFo{\vert{"w"_{\sym{i}}}, \matrix{M}\matrixDotSymbol \groupHomomorphism{ \phi }(\card{c_{\sym{i}}})} \).
We then go on to explore these new states in a first-in last-out fashion, stopping when we reach some depth. Sometimes we will encounter a state that we have created before -- this is to say, we will find two different paths in the fundamental quiver that produce the same state -- but we can avoid re-exploring these old states by caching them in a suitable data structure.
By storing only states and their adjacency, and not entire paths, we avoid performing an exponential amount of computation as the number of visited states increases (this is a form of so-called dynamic programming).
The graph that we produce in this exploration has vertices given by states \( \TuFo{\vert{v}, \matrix{M}} \) and edges given by transitions \( \tde{\TuFo{\vert{v}, \matrix{M}}}{\TuFo{\vert{\primed{v}}, \matrix{\primed{M}}}}{\card{\card{c}_{\sym{i}}}} \), where \( \matrix{\primed{M}} = \matrix{M}\matrixDotSymbol \groupHomomorphism{ \phi }(\card{c}_{\sym{i}}) \) and \( \elemOf{\tde{\vert{v}}{\vert{\primed{v}}}{\card{\card{c}_{\sym{i}}}}}{\edgeList(\quiver{F})} \).
In other contexts, a graph so produced is variously known as a state-transition graph, multiway graph, or in the group-theory context, a Cayley graph. In our context, these graphs are quivers, since the have an additional cardinal structure in which each edge is labeled with the cardinal we took to generate that particular state. Moreover, these quivers represent particular quotients of path quivers. When the quotient is in terms of a homomorphism into a translation group, we'll simply use the term lattice quivers.
Notation #
We will denote the quiver generated by exploring fundamental quiver \( \quiver{F} \), starting at vertex \( \vert{x} \), using the affine path valuation \( \affineModifier{\pathHomomorphism{ \phi }} \) induced by group homomorphism \( \functionSignature{\groupHomomorphism{ \phi }}{\wordGroup{\quiver{F}}}{\generalLinearGroup{\sym{n}}{\field{K}}} \), to depth \( \sym{d} \), with the expression:
\[ \latticeBFS{\quiver{F},\vert{x},\groupHomomorphism{ \phi },\sym{d}} \]By setting \( \sym{d} = \infty \) we represent the "ongoing breadth-first search" that typically does not ever terminate, which we interpret as computing the full forward path quiver quotient to arbitrary depth:
\[ \compactQuotient{\quiver{F}}{\vert{x}}{\groupHomomorphism{ \phi }} = \limit{\latticeBFS{\quiver{F},\vert{x},\groupHomomorphism{ \phi },\sym{d}}}{\sym{d} \to \infty } \]This limit is true in the sense that every vertex / edge of the quotient will eventually be generated by the search for some sufficiently large \( \sym{d} \), and conversely every vertex / edge generated by the search corresponds to some vertex / edge of the quotient.
Translation matrices #
While cardinal matrices \( \groupHomomorphism{ \phi }(\card{c_{\sym{i}}}) \) are in general \( \sym{n}\times \sym{n} \), we will be limiting ourselves to translation matrices, which can be put into a simple upper triangular form as follows:
\[ \translationVector{\sym{x}}\defEqualSymbol {\begin{pmatrix}1&\sym{x}\\0&1\end{pmatrix}}\quad \translationVector{\sym{x},\sym{y}}\defEqualSymbol {\begin{pmatrix}1&0&\sym{x}\\0&1&\sym{y}\\0&0&1\end{pmatrix}}\quad \translationVector{\sym{x},\sym{y},\sym{z}}\defEqualSymbol {\begin{pmatrix}1&0&0&\sym{x}\\0&1&0&\sym{y}\\0&0&1&\sym{z}\\0&0&0&1\end{pmatrix}}\quad \elSy \]These matrices have the property that:
\[ \begin{aligned} \translationVector{\sym{x}}\matrixDotSymbol \translationVector{\primed{\sym{x}}}&= \translationVector{\sym{x} + \primed{\sym{x}}}\\ \translationVector{\sym{x},\sym{y}}\matrixDotSymbol \translationVector{\primed{\sym{x}},\primed{\sym{y}}}&= \translationVector{\sym{x} + \primed{\sym{x}},\sym{y} + \primed{\sym{y}}}\\ \translationVector{\sym{x},\sym{y},\sym{z}}\matrixDotSymbol \translationVector{\primed{\sym{x}},\primed{\sym{y}},\primed{\sym{z}}}&= \translationVector{\sym{x} + \primed{\sym{x}},\sym{y} + \primed{\sym{y}},\sym{z} + \primed{\sym{z}}}\end{aligned} \]Line lattice #
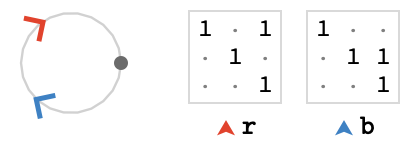
To kick things off let’s look at probably the simplest possible fundamental quiver: a 1-bouquet quiver \( \bindCards{\bouquetQuiver{1}}{\reFo{\card{r}}} \).
We'll associate its only cardinal \( \reFo{\card{r}} \) with a \( 2 \times 2 \) matrix, representing a generator of the group \( \mathbb{Z} \).

Now, because this quiver only has one vertex, all of the paths in \( \quiver{F} \) are trivially composable, and the path groupoid \( \pathGroupoid{\quiver{F}} \) is isomorphic to the word group \( \wordGroup{\quiver{F}} \) on one cardinal, which is itself isomorphic to \( \mathbb{Z} \) -- since we just count how many times that cardinal appears in a given word.
We wish to generate the lattice quiver, which is the quotient \( \compactQuotient{\bindCardSize{\bouquetQuiver{1}}{\reFo{\card{r}}}}{\vert{o}}{\bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}}} \), where \( \bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}} \) is the group homomorphism \( \functionSignature{\function{\bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}}}}{\wordGroup{\quiver{F}}}{\generalLinearGroup{2}{\ring{\mathbb{Z}}}} \) defined by:
\[ \bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1}}} \]We can traverse the single fundamental quiver edge \( \tde{\vert{x}}{\vert{x}}{\reFo{\card{r}}} \) in the forward or reverse direction, so we can reach two states from the initial state. We continue this process until we have reached the specified traversal depth.
Here’s the lattice quiver for our simple fundamental quiver (the origin vertex, corresponding to state \( \TuFo{\vert{o}, \matrix{I}} \), is shown larger):
Let's label these vertices with their corresponding matrices to see better what is going on:

Note that the top-right entry of each matrix is effectively acting as a 1D coordinate.
We state without proof:
\[ \bindCardSize{\subSize{\lineQuiver }{ \infty }}{\reFo{\card{r}}}\isomorphicSymbol \compactQuotient{\bindCardSize{\bouquetQuiver{1}}{\reFo{\card{r}}}}{\vert{o}}{\bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}}} \]Additionally, when explored to finite depth, we have:
\[ \bindCardSize{\subSize{\lineQuiver }{2 \, \sym{n} + 1}}{\reFo{\card{r}}}\isomorphicSymbol \latticeBFS{\bindCardSize{\bouquetQuiver{1}}{\reFo{\card{r}}},\vert{o},\bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}},\sym{n}} \]Animation #
We can demonstrate the gradual building of the infinite line lattice by breadth first search:

Square lattice #
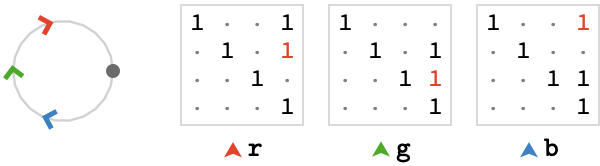
Let’s move on to a two-dimensional lattice quiver. We’ve added a cardinal \( \blFo{\card{b}} \) to the fundamental quiver:
Notice that the cardinal matrices are the two unit translation matrices for \( \mathbb{Z}^2 \):
\[ \bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}},\blFo{\card{b}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,0}},\mto{\blFo{\card{b}}}{\translationVector{0,1}}} \]As you would expect, the lattice quiver this generates is a 2D grid:

Again, notice the 2D “translation coordinates” that the representation matrices contain:

Note that negative integers are displayed as red, rather than with a minus sign.
Since all our matrices are translation matrices, we can extract the coordinate vector from each matrix for a cleaner graphic:

Again, we state without proof:
\[ \bindCardSize{\subSize{\squareQuiver }{ \infty }}{\reFo{\card{r}},\blFo{\card{b}}}\isomorphicSymbol \compactQuotient{\bindCardSize{\bouquetQuiver{2}}{\reFo{\card{r}},\blFo{\card{b}}}}{\vert{o}}{\bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}},\blFo{\card{b}}}} \]Animation #
We can demonstrate the gradual building of the infinite square lattice by breadth first search:

Animation #
We can animate the process by which the full path quiver on the fundamental quiver is quotiented to become the square lattice quiver. This is shown by starting with the layout of the path quiver, and gradually moving the multiple vertices which share a path value into each other:
Paths and relations #
Although the point should be quite clear, let's visualize how vertices in the lattice quiver correspond to paths in the fundamental quiver that have the same value.
Here we have two paths with words \( \word{\reFo{\card{r}}}{\blFo{\card{b}}} \) and \( \word{\blFo{\card{b}}}{\reFo{\card{r}}} \) in the fundamental quiver, shown on the right. The fact that terminate at the same vertex in the lattice quiver reflects the fact that the values of those two paths are the same: \( \matrix{M_{\reFo{\card{r}}}}\matrixDotSymbol \matrix{M_{\blFo{\card{b}}}} = \matrix{M_{\blFo{\card{b}}}}\matrixDotSymbol \matrix{M_{\reFo{\card{r}}}} \). This must be true because the cardinal matrices \( \matrix{M_i} \) represent an Abelian group (namely a translation group) and in fact this path diagram is the defining relation of this particular group.
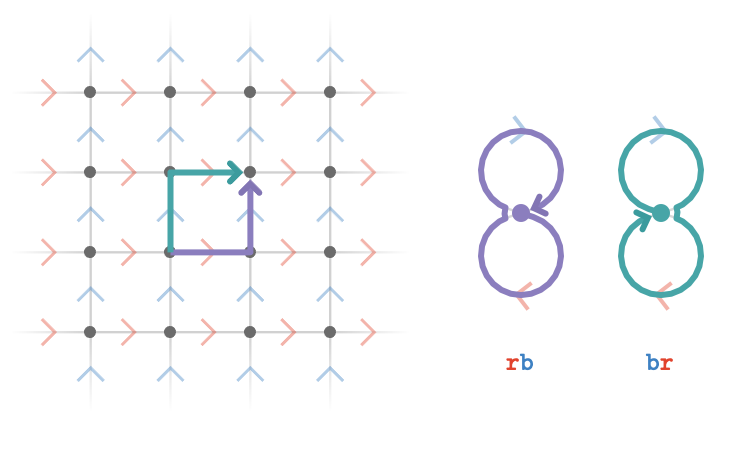
We'll call this a path relation of a lattice quiver, and write it algebraically as \( \word{\reFo{\card{r}}}{\blFo{\card{b}}}\pathIso \word{\blFo{\card{b}}}{\reFo{\card{r}}} \). The symbol \( \pathIso \) is understood to mean that the two paths with the given path words that share a tail vertex, also share a head vertex in the lattice quiver.
Triangular lattice #
Perhaps a more interesting example of path relations comes from the following lattice quiver with three cardinals:
Here, the cardinal matrices are the following translations of \( \mathbb{Z}^3 \):
\[ \bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,-1,0}},\mto{\grFo{\card{g}}}{\translationVector{0,1,-1}},\mto{\blFo{\card{b}}}{\translationVector{-1,0,1}}} \]This generates a triangular lattice, shown here to depth 3:
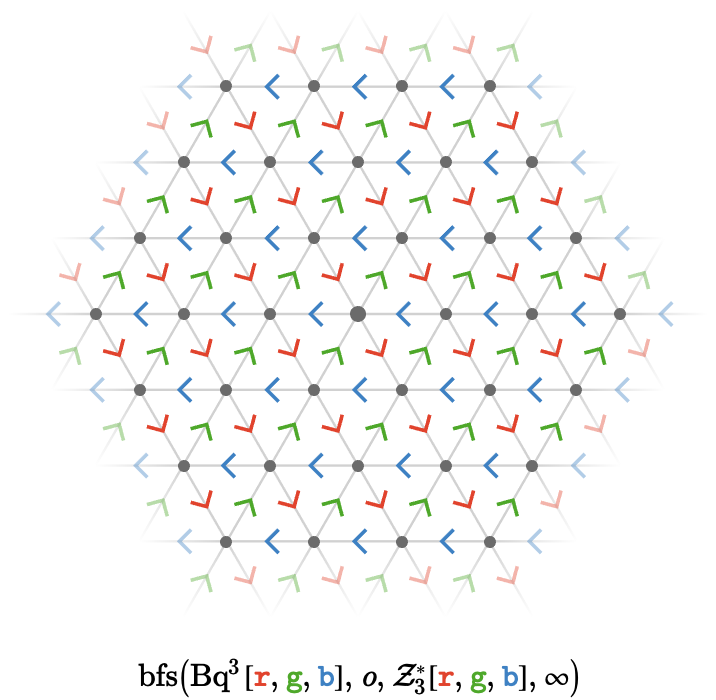
Although these matrices represent translations in \( \mathbb{Z}^3 \), they are not linearly independent, and so their action is two dimensional, yielding a planar lattice quiver.
Let's visualize their translation vectors:

We can also look at a path diagram for the triangular lattice:
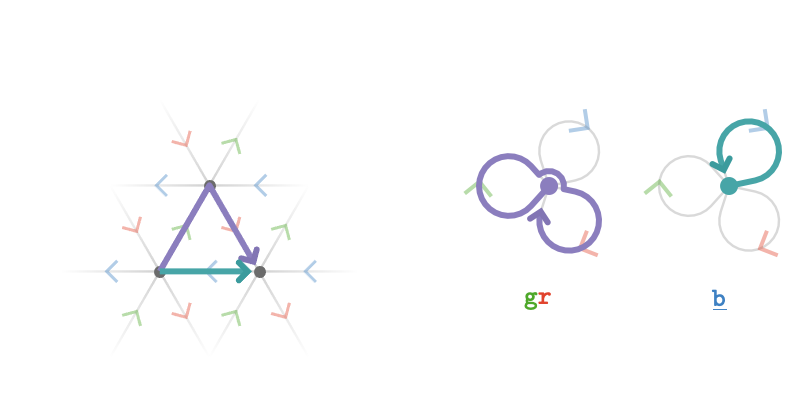
Again, the fact that \( \word{\grFo{\card{g}}}{\reFo{\card{r}}}\pathIso \word{\blFo{\ncard{b}}} \) reflects the property of the cardinal matrices that \( \matrix{M_{\reFo{\card{r}}}}\matrixDotSymbol \matrix{M_{\grFo{\card{g}}}} = \inverse{\matrix{M_{\blFo{\card{b}}}}} \), or more simply that \( \matrix{M_{\reFo{\card{r}}}}\matrixDotSymbol \matrix{M_{\grFo{\card{g}}}}\matrixDotSymbol \matrix{M_{\blFo{\card{b}}}} = \matrix{I} \).
So, while we pulled these matrices out of a hat, we can interpret them as encoding the following path relations:
\[ \list{\word{\grFo{\card{g}}}{\reFo{\card{r}}}\pathIso \word{\reFo{\card{r}}}{\grFo{\card{g}}},\word{\grFo{\card{g}}}{\blFo{\card{b}}}\pathIso \word{\blFo{\card{b}}}{\grFo{\card{g}}},\word{\blFo{\card{b}}}{\reFo{\card{r}}}\pathIso \word{\reFo{\card{r}}}{\blFo{\card{b}}},\word{\reFo{\card{r}}}{\grFo{\card{g}}}{\blFo{\card{b}}}\pathIso \word{1}} \]The full set of relations can be illustrated as path diagrams as follows:
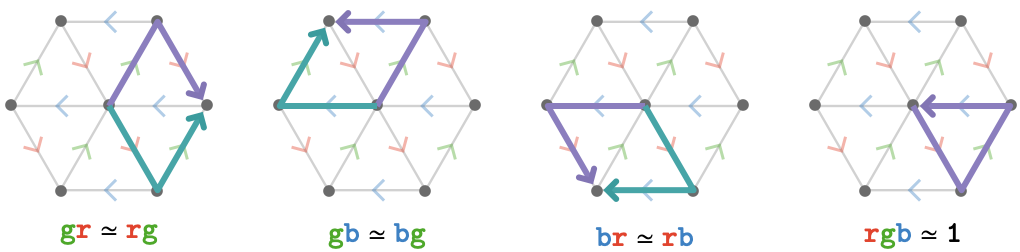
Lastly, we again state without proof:
\[ \bindCardSize{\subSize{\triangularQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\isomorphicSymbol \compactQuotient{\bindCardSize{\bouquetQuiver{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}}{\vert{o}}{\bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}} \]Connection to Cayley quivers #
We've given a construction of some familiar quivers as linear path representations, which are particular path quotients \( \compactQuotient{\quiver{F}}{\vert{x}}{\groupHomomorphism{ \phi }} \) induced by group homomorphisms of the form \( \functionSignature{\groupHomomorphism{ \phi }}{\wordGroup{\quiver{F}}}{\generalLinearGroup{\sym{n}}{\field{K}}} \). These homomorphism are uniquely defined by choices of invertible matrices \( \matrix{M_{\sym{i}}} \) for each cardinal \( \elemOf{\card{c_{\sym{i}}}}{\cardinalList(\quiver{F})} \), letting us write \( \groupHomomorphism{ \phi } = \assocArray{\mto{\card{c}_1}{\matrix{M_1}},\elSy,\mto{\card{c}_{\sym{k}}}{\matrix{M_{\sym{k}}}}} \).
It's important to emphasize how this construction yields a Cayley quiver in the special case that \( \quiver{F} \) is a bouquet quiver. This is because the path groupoid of a bouquet quiver is just the word group (as all paths can be composed), so we can write:
\[ \pathGroupoid{\quiver{F}} = \wordGroup{\quiver{F}} \]Hence, for bouquet quivers a (linear) path representation \( \functionSignature{\groupoidHomomorphism{ \mu }}{\pathGroupoid{\quiver{F}}}{\generalLinearGroup{\sym{n}}{\field{K}}} \) is just a group homomorphism \( \functionSignature{\groupoidHomomorphism{ \mu }}{\wordGroup{\quiver{F}}}{\generalLinearGroup{\sym{n}}{\field{K}}} \). The image of \( \groupoidHomomorphism{ \mu } \) is then a subgroup \( \groupoidHomomorphism{ \mu }(\wordGroupSymbol ) \subseteq \generalLinearGroup{\sym{n}}{\field{K}} \) generated by \( \sym{J} = \setConstructor{\groupoidHomomorphism{ \mu }(\card{c}_{\sym{i}})}{1 \le \sym{i} \le \sym{k}} \). Then the regular action of this subgroup yields a Cayley quiver:
\[ \bindCayleyQuiver{\groupHomomorphism{ \mu }(\wordGroupSymbol )}{\sym{J}} \]Why is this quiver the same as that produced by \( \compactQuotient{\quiver{F}}{\vert{o}}{\pathHomomorphism{ \mu }}\congruentSymbol \latticeBFS{\quiver{F},\vert{o},\pathHomomorphism{ \mu }, \infty } \)? Since \( \quiver{F} \) only has one vertex \( \vert{o} \), the states \( \TuFo{\vert{v}, \matrix{M}} \) involved in the bfs construction all share the fundmanetal vertex \( \vert{v} = \vert{o} \). Hence vertices of the multiway graph are uniquely described by matrices \( \matrix{M} \), and edges \( \tde{\matrix{M}}{\matrix{\primed{M}}}{\card{c_{\sym{i}}}} \) exist iff \( \matrix{\primed{M}} = \matrix{M}\matrixDotSymbol \function{ \mu }(\card{c_{\sym{i}}}) \). This is by definition a right self-action of the subgroup \( \pathHomomorphism{ \mu }(\wordGroupSymbol ) \), with generators \( \sym{J} = \setConstructor{\groupoidHomomorphism{ \mu }(\card{c}_{\sym{i}})}{1 \le \sym{i} \le \sym{k}} \), as required:
\[ \bindCayleyQuiver{\pathHomomorphism{ \mu }(\wordGroupSymbol )}{\sym{J}} = \compactQuotient{\quiver{F}}{\vert{o}}{\pathHomomorphism{ \mu }} \]Summary #
Named group homomorphisms #
We collect the group homomoprhisms \( \groupoidFunction{ \phi } \) used in the linear path representations above:
\[ \begin{aligned} \bindCardSize{\translationWordHomomorphism{1}}{\reFo{\card{r}}}&\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1}}}\\ \bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}},\blFo{\card{b}}}&\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,0}},\mto{\blFo{\card{b}}}{\translationVector{0,1}}}\\ \bindCardSize{\translationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}&\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,0,0}},\mto{\grFo{\card{g}}}{\translationVector{0,1,0}},\mto{\blFo{\card{b}}}{\translationVector{0,0,1}}}\\ \bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}&\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,-1,0}},\mto{\grFo{\card{g}}}{\translationVector{0,1,-1}},\mto{\blFo{\card{b}}}{\translationVector{-1,0,1}}}\end{aligned} \]Homomorphisms and presentations #
We can naturally associate these group homomorphisms with particular named group presentations that generate the same lattice quivers as their Cayley quivers (we discussed this from a slightly different perspective above).
For example, the homomorphism \( \functionSignature{\function{\starTranslationWordHomomorphism{3}}}{\wordGroup{\quiver{3}}}{\generalLinearGroup{3}{\ring{\mathbb{Z}}}} \) defined by \( \bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,-1,0}},\mto{\grFo{\card{g}}}{\translationVector{0,1,-1}},\mto{\blFo{\card{b}}}{\translationVector{-1,0,1}}} \) is associated with the presentation \( \starTranslationPresentation{3} \) defined by \( \bindCardSize{\starTranslationPresentation{3}}{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\grFo{g}}},\groupCommutator{\groupGenerator{\grFo{g}}}{\groupGenerator{\blFo{b}}},\groupGenerator{\reFo{r}}\iGmult \groupGenerator{\grFo{g}}\iGmult \groupInverse{\groupGenerator{\blFo{b}}}} \).
Specifically, the image \( \function{\starTranslationWordHomomorphism{3}}(\wordGroup{\quiver{3}}) \) is a subgroup of \( \generalLinearGroup{3}{\ring{\mathbb{Z}}} \) that is isomorphic to the group presented by \( \starTranslationPresentation{3} \), with the isomorphism sending cardinals \( \reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}} \) (which are the generators) of \( \wordGroup{\quiver{3}} \) to the generators \( \groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}} \) used by the presentation \( \starTranslationPresentation{3} \). This isomorphism makes \( \starTranslationWordHomomorphism{3} \) into the "identity homomorphism":
\[ \bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\isomorphicSymbol \assocArray{\mto{\reFo{\card{r}}}{\groupGenerator{\reFo{r}}},\mto{\grFo{\card{g}}}{\groupGenerator{\grFo{g}}},\mto{\blFo{\card{b}}}{\groupGenerator{\blFo{b}}}} \]Transitive lattice quivers #
These named homomorphisms and presentations allows us to express how to generate the various transitive lattice quivers succintly in the following table:
| name | quiver | fun. quiver | homomorphism | presentation |
|---|---|---|---|---|
| line quiver | \( \subSize{\lineQuiver }{ \infty } \) | \( \bouquetQuiver{1} \) | \( \functionSignature{\function{\translationWordHomomorphism{1}}}{\wordGroup{\quiver{1}}}{\group{\mathbb{Z}}} \) | \( \translationPresentation{1} \) presenting \( \group{\mathbb{Z}} \) |
| square quiver | \( \subSize{\squareQuiver }{ \infty } \) | \( \bouquetQuiver{2} \) | \( \functionSignature{\function{\translationWordHomomorphism{2}}}{\wordGroup{\quiver{2}}}{\group{\power{\group{\mathbb{Z}}}{2}}} \) | \( \translationPresentation{2} \) presenting \( \group{\power{\group{\mathbb{Z}}}{2}} \) |
| triangular quiver | \( \subSize{\triangularQuiver }{ \infty } \) | \( \bouquetQuiver{3} \) | \( \functionSignature{\function{\starTranslationWordHomomorphism{3}}}{\wordGroup{\quiver{3}}}{\group{\power{\group{\mathbb{Z}}}{3}}} \) | \( \starTranslationPresentation{3} \) presenting \( \group{\power{\group{\mathbb{Z}}}{2}} \) |
| cubic quiver | \( \subSize{\cubicQuiver }{ \infty } \) | \( \bouquetQuiver{3} \) | \( \functionSignature{\function{\translationWordHomomorphism{3}}}{\wordGroup{\quiver{3}}}{\group{\power{\group{\mathbb{Z}}}{3}}} \) | \( \translationPresentation{3} \) presenting \( \group{\power{\group{\mathbb{Z}}}{3}} \) |
| grid quiver | \( \gridQuiver{\sym{k}} \) | \( \bouquetQuiver{\sym{k}} \) | \( \functionSignature{\function{\translationWordHomomorphism{\sym{k}}}}{\wordGroup{\quiver{\sym{k}}}}{\group{\power{\group{\mathbb{Z}}}{\sym{k}}}} \) | \( \translationPresentation{\sym{k}} \) presenting \( \group{\power{\group{\mathbb{Z}}}{\sym{k}}} \) |
Why? #
This interrelationship between quotients, Cayley quivers, and presentations may seem rather pedantic -- hardly worth all the notation and machinery. And perhaps this is true for transitive quivers! But as we mentioned in Action groupoids, the benefit is that we can generalize beyond groups and their Cayley quivers into areas where some of these constructions may be better suited, and provide better intuition, than others.
For example, the next section, we will consider more complex fundamental quivers, which will allow us to construct the hexagonal quiver, among others.