Path quotients #
Motivation #
In this section, we're going to set up a construction that we'll use in the next section to build infinite but highly regular quivers from simpler finite quivers. The construction uses a path valuation (a function on paths) to define when two paths on a finite quiver \( \quiver{Q} \) are equivalent. By identifying equivalent paths, we will effectively "glue together" sets of vertices of the infinite forward path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{v}} \), turning it from an infinite tree into a so-called lattice quiver.
This gluing procedure is a very common idea in abstract algebra, where it generally goes by the name of a quotient. Hence we are defining a path quotient.
Note: if this section is too abstract for your taste, you can safely skip ahead to the next section.
Recap #
There are by now several moving pieces, so let's do a quick recap:
From Path groupoids, we saw that a path \( \path{P} = \paren{\pathWord{\vert{h}}{\wordSymbol{W}}{\vert{t}}} \) is uniquely determined by its initial (or final) vertex and its path word \( \wordSymbol{W} \). We can define the function \( \wordOf(\path{P})\defEqualSymbol \wordSymbol{W} \) that sends a path to its path word. Two different paths can have the same path word. The path groupoid \( \pathGroupoid{\quiver{Q}} \) is the groupoid whose elements are paths in \( \quiver{Q} \), and whose multiplication is path composition.
From Path quivers, we defined vertices of the forward path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{v}} \) to correspond to the paths of \( \quiver{Q} \) that start at \( \vert{v} \):
\[ \vertexList(\forwardPathQuiver{\quiver{Q}}{\vert{x}})\defEqualSymbol \pathList(\quiver{Q},\vert{v},\blSy) \]The vertices of the more general affine path quiver \( \pathQuiver{\quiver{Q}} \) correspond to all paths of \( \quiver{Q} \), regardless of where they start:
\[ \vertexList(\pathQuiver{\quiver{Q}})\defEqualSymbol \pathList(\quiver{Q},\blSy,\blSy) \]By moving to the more general setting of the affine path quiver, we gain an important property: the affine path quiver \( \pathQuiver{\quiver{Q}} \) is closed under path reversal. In comparison, reversing a path \( \elemOf{\path{P}}{\forwardPathQuiver{\quiver{Q}}{\vert{v}}} \), only yields another path in \( \forwardPathQuiver{\quiver{Q}}{\vert{v}} \) when \( \headVertex(\path{P}) = \tailVertex(\path{P}) = \vert{v} \), in other words, when the path is a cycle.
In either cases, the edges of a path quiver correspond to retractions or extensions of paths by following a cardinal available at the head of the path, giving us the cardinal structure of the path quiver.
We see then that \( \pathGroupoid{\quiver{Q}} \) and \( \pathQuiver{\quiver{Q}} \) are closely related: the elements of the path groupoid \( \pathGroupoid{\quiver{Q}} \) are vertices of the path quiver \( \pathQuiver{\quiver{Q}} \).
Path valuations #
We now define a path valuation \( \functionSignature{\groupoidHomomorphism{ \mu }}{\pathGroupoid{\quiver{Q}}}{\group{V}} \) to be a groupoid homomorphism from the path groupoid \( \pathGroupoid{\quiver{Q}} \) to an arbitrary group \( \group{V} \), which we call the value group. We say it assigns a path value \( \groupoidHomomorphism{ \mu }(\path{P}) \) to each path \( \elemOf{\path{P}}{\pathGroupoid{\quiver{Q}}} \).
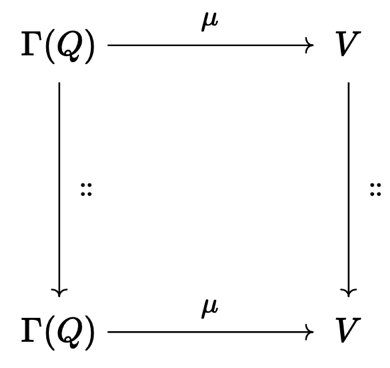
A groupoid homomorphism simply means that \( \pathCompose{\path{P_1}}{\path{P_2}} = \groupoidHomomorphism{ \mu }(\path{P_1})\gmult \groupoidHomomorphism{ \mu }(\path{P_2}) \); this amounts to saying that the values of paths are “compatible” with composition: taking values of two paths \( \path{P_1},\path{P_2} \) and multiplying them in the value group gives the same result as taking the value of the composition of the two paths. This situation is depicted in the following diagram (the vertical arrows actually refer to binary functions, but you get the idea):
Example: word #
Perhaps the simplest path valuation of all is given by \( \wordOf \), the function that takes a path to its path word, where that path word is seen as an element of the word group, written \( \wordGroup{\quiver{Q}} \), which we defined in Path homomorphisms:
\[ \functionSignature{\wordOf}{\pathGroupoid{\quiver{Q}}}{\wordGroup{\quiver{Q}}} \]We saw earlier that the function \( \wordOf \) is a groupoid homomorphism. But it is not in general surjective: we can form words \( \elemOf{\wordSymbol{W}}{\wordGroup{\quiver{Q}}} \) that might not correspond to the path word of any path in \( \quiver{Q} \).
Example: signed length #
As a less trivial example, we can take \( \groupoid{V} \) to be the group(oid) of the integers numbers \( (\mathbb{Z},+ ) \) under addition, and the valuation \( \pathMap{ \mu } \) to be the signed length of a path, written \( \signedLength \), in which cardinals count as +1 and inverses of cardinals count as \( -1 \).
Then \( \functionSignature{\signedLength}{\pathGroupoid{\quiver{Q}}}{\group{\mathbb{Z}}} \) is indeed a homomorphism, since the signed length of the composition of two paths is the sum of their signed lengths: \( \signedLength(\pathCompose{\path{P_1}}{\path{P_2}}) = \signedLength(\path{P_1}) + \signedLength(\path{P_2}) \). Empty paths are sent to \( \groupElement{0} \), which is of course the identity element of \( \group{\mathbb{Z}} \).
As this example shows, the homomorphism can forget information about the original path, but whatever information it retains must be "composable".
Affine path valuations #
A family of path valuations, called affine path valuations, can be constructed from group homomorphisms of the form \( \functionSignature{\groupHomomorphism{ \phi }}{\wordGroup{\quiver{Q}}}{\group{V}} \).
The group homomorphism \( \groupHomomorphism{ \phi } \) induces a path valuation \( \functionSignature{\pathMap{\affineModifier{\groupHomomorphism{ \phi }}}}{\pathQuiver{\quiver{Q}}}{\group{V}} \) in the following way:
\[ \pathMap{\affineModifier{\groupHomomorphism{ \phi }}}(\pathWord{\vert{x}}{\word{\card{c_1}}{\card{\elSy}}{\card{c_{\sym{n}}}}}{\vert{y}})\defEqualSymbol \indexProd{\groupHomomorphism{ \phi }(\card{c_{\sym{i}}})}{\sym{i} = 1}{\sym{n}} = \groupHomomorphism{ \phi }(\card{c_1})\gmult \elSy\gmult \groupHomomorphism{ \phi }(\card{c_{\sym{n}}}) \]In English: an affine path valuation \( \affineModifier{\groupHomomorphism{ \phi }} \) calculates the value \( \pathMap{\affineModifier{\groupHomomorphism{ \phi }}}(\path{P}) \) of a path \( \path{P} = \parenPathWord{\vert{x}}{\word{\card{c_1}}{\card{\elSy}}{\card{c_{\sym{n}}}}}{\vert{y}} \) as the group product of the values \( \groupHomomorphism{ \phi }(\card{c_{\sym{i}}}) \) in its path word \( \word{\card{c_1}}{\card{\elSy}}{\card{c_{\sym{n}}}} \).
What is natural about constructing value functions in this way is that they are automatically groupoid homomorphisms due to the associativity of the underlying groupoid multiplication in the group \( \group{V} \). We use the word affine because this construction forces the valuation to ignore the head or tail of a path: it only depends on the "cardinal content" of the path.
We've already seen two examples of affine path valuations: it is easy to verify that the signed length \( \signedLength \) is an affine path valuation given by \( \groupHomomorphism{ \phi }(\card{c}) = 1 \) for \( \elemOf{\card{c}}{\cardinalList(\quiver{Q})} \), which of course implies that \( \groupHomomorphism{ \phi }(\inverted{\card{c}}) = -1 \). It’s also easy to see that the function \( \functionSignature{\wordOf}{\pathGroupoid{\quiver{Q}}}{\wordGroup{\quiver{Q}}} \) is an affine path valuation, induced by the identity group homomorphism on \( \wordGroup{\quiver{Q}} \).
Semivaluations #
We can obtain a wider range of path valuations if we relax our requirement that a valuation be a groupoid homomorphism. Forgetting the inverse operation of our groupoids (path and value), and considering them as so-called semigroupoids with identity, it becomes easier to construct path valuations, since semigroupoid homomorphism is a weaker requirement. We'll call these path semivaluations.
An example of a path semivaluation is the intuitive function \( \functionSignature{\length}{\pathGroupoid{\quiver{Q}}}{\semiring{\na}} \) that measures the ordinary length of a path, which is the length of its path word:
\[ \length(\pathWord{\vert{x}}{\word{\card{c_1}}{\card{\elSy}}{\card{c_{\sym{n}}}}}{\vert{y}})\defEqualSymbol \sym{n} \]And similar to the affine path valuation case, we can use a semigroup homomorphism \( \functionSignature{\groupHomomorphism{ \phi }}{\wordGroup{\quiver{Q}}}{\quiver{S}} \) to induce a path semivaluation \( \functionSignature{\function{\affineModifier{\groupHomomorphism{ \phi }}}}{\pathGroupoid{\quiver{Q}}}{\quiver{S}} \).
Repeating the earlier story with \( \signedLength \), \( \length \) can be seen as being induced by the semigroup homomorphism \( \function{ \phi }(\card{c}) = \function{ \phi }(\inverted{\card{c}}) = 1 \). Unsurprisingly, we can also construct "cardinal-sensitive" variants of \( \length \), which assign \( \function{ \phi _{\sym{j}}}(\card{c_{\sym{i}}}) = \delta _{i,j} \).
Notation #
To ease the notation, we will often write quotients involving affine path valuations in the following more compact notation:
\[ \compactQuotient{\quiver{F}}{\vert{v}}{\groupHomomorphism{ \phi }}\defEqualSymbol \quotient{\forwardPathQuiver{\quiver{Q}}{\vert{v}}}{\affineModifier{\groupHomomorphism{ \phi }}} \]Path quotients #
Path valuations will allow us to construct path quotients.
Path quotients are a simple but powerful way of deriving quivers from other quivers, whenever we have a path valuation \( \pathMap{ \mu } \). We’ll shortly use this to begin constructing discrete geometries.
Let \( \quiver{F} \) be a quiver and \( \functionSignature{\groupoidHomomorphism{ \mu }}{\pathQuiver{\quiver{F}}}{\group{V}} \) be a path valuation on \( \quiver{F} \). The forward quotient \( \quiver{G} = \quotient{\forwardPathQuiver{\quiver{F}}{\vert{x}}}{\groupoidHomomorphism{ \mu }} \) is the quiver defined as follows:
-
a vertex \( \elemOf{\vert{v}}{\vertexList(\quiver{G})} \) is the equivalence class of paths beginning at \( \vert{x} \) that have the value \( \groupoidElement{v} \) under \( \pathMap{ \mu } \), in other words the set \( \inverse{\groupoidHomomorphism{ \mu }}(\vert{v}) \subseteq \forwardPathQuiver{\quiver{F}}{\vert{x}} \)
-
an edge \( \tde{\vert{u}}{\vert{v}}{\card{c}} \) exists in \( \quiver{G} \) iff one of the paths in \( \function{\inverse{\pathMap{ \mu }}}(\vert{v}) \) is an extension of one of the paths in \( \function{\inverse{\pathMap{ \mu }}}(\vert{u}) \) by the cardinal \( \elemOf{\card{c}}{\cardinalList(\quiver{F})} \).
Example: signed length #
To illustrate a path quotient, we’ll use the following tree quiver with root vertex \( \vert{o} \) shown at the top:
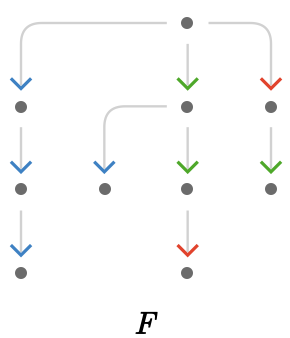
We’ll construct the quotient \( \quotient{\forwardPathQuiver{\quiver{F}}{\vert{o}}}{\signedLength} \) using the signed length \( \signedLength \) path valuation we introduced earlier:
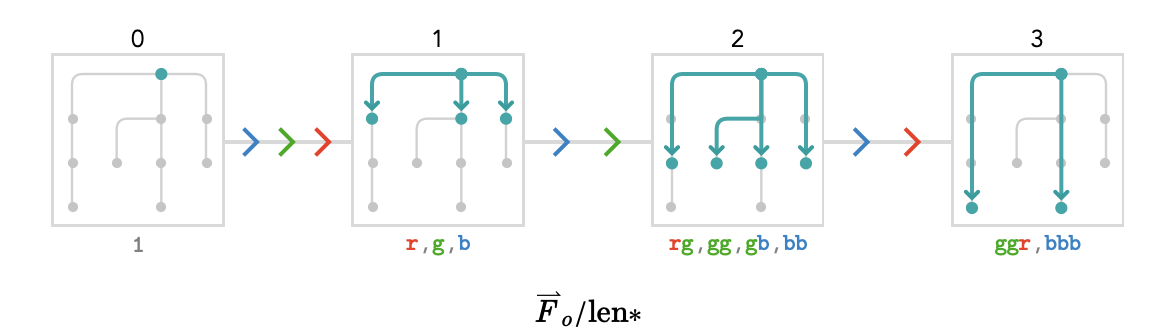
We’ve drawn the equivalence classes of paths by just superimposing those paths on each diagram.
By definition, there is one class for each value in \( \signedLength(\pathGroupoid{\quiver{F}}) \), namely for each length of path. These values are shown in a label above each class, starting with 0 on the left and ending with 3 on the right.
A technicality worth mentioning: the cardinal \( \grFo{\card{g}} \) should occur twice between the length 1 and length 2 classes, since there are two paths that can be extended by \( \grFo{\card{g}} \), being \( \de{\word{\reFo{\card{r}}}}{\word{\reFo{\card{r}}}{\grFo{\card{g}}}} \) and \( \de{\word{\grFo{\card{g}}}}{\word{\grFo{\card{g}}}{\grFo{\card{g}}}} \). But we ignore this multiplicity, for the reason that this results in no violation of the local uniqueness property we require of quivers.
Example: cardinal-sensitive length #
Let’s perform a similar quotient, except using the cardinal-sensitive signed length \( \signedLength_{\grFo{\card{g}}} \) we defined earlier. This will measure a path length in which only the cardinal \( \grFo{\card{g}} \) counts towards the total.
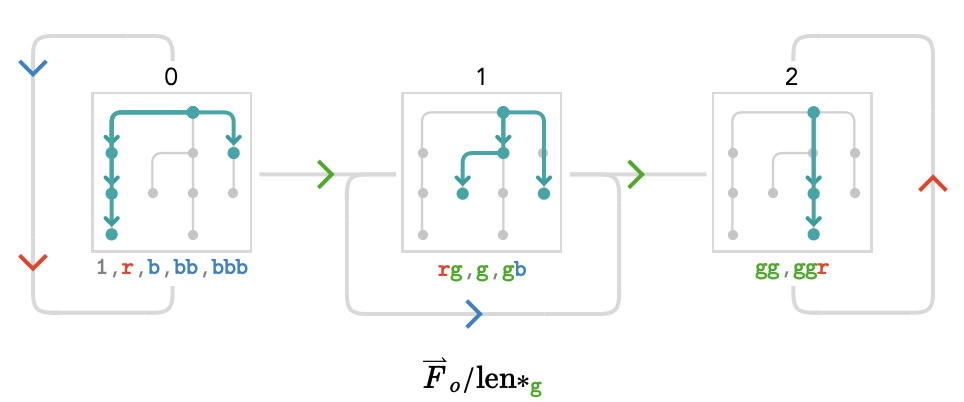
As an exercise, I suggest checking the existence of every cardinal in the path quiver above, and make sure the equivalence classes are as you suspect.
Example: modulo signed length #
In the last example, we will look at the signed length modulo an integer. We'll apply this path valuation to the path quiver of a 1-bouquet \( \quiver{B} = \bindCards{\bouquetQuiver{1}}{\reFo{\card{r}}} \):
As we saw before, \( \forwardPathQuiver{\quiver{B}}{\vert{o}} = \bindCardSize{\subSize{\lineQuiver }{ \infty }}{\reFo{\card{r}}} \). Here we show a fragment of \( \forwardPathQuiver{\quiver{B}}{\vert{o}} \), with the particular paths illustrated:

We'll now form the quotient \( \quotient{\forwardPathQuiver{\quiver{B}}{\vert{o}}}{\paren{\modLabeled{\signedLength}{3}}} \):
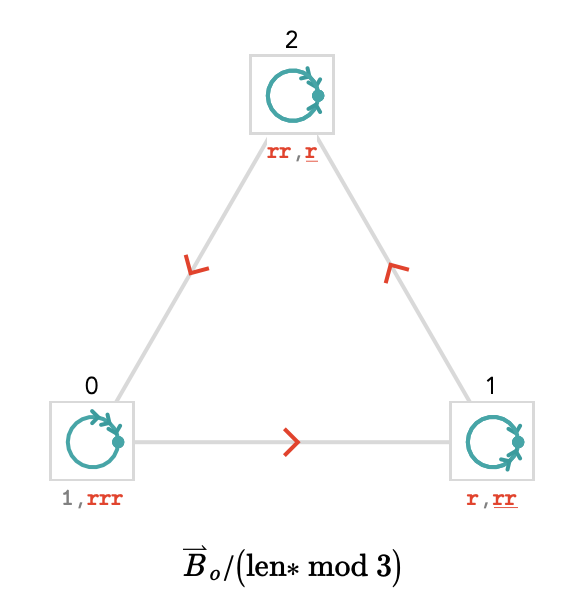
As with any infinite path quiver, the equivalence classes shown above, namely \( \list{\word{\card{1}},\word{\reFo{\card{r}}}{\reFo{\card{r}}}{\reFo{\card{r}}}} \), \( \list{\word{\reFo{\card{r}}},\word{\reFo{\ncard{r}}}{\reFo{\ncard{r}}}} \), \( \list{\word{\reFo{\card{r}}}{\reFo{\card{r}}},\word{\reFo{\ncard{r}}}} \) are just fragments of infinite sets, of the form:
\[ \setConstructor{\repeatedPower{\reFo{\card{r}}}{3 \, \sym{n} + \sym{m}}}{\elemOf{\sym{n}}{\mathbb{Z}}} \]where \( \elemOf{\sym{m}}{\list{0,1,2}} \) is the value: the signed cardinal length modulo 3.