Action groupoids #
Introduction #
In this section, we'll further explore the connection between Transitive quivers and groups that we started in Cayley quivers. We'll see that a transitive quiver that is the Cayley quiver of a group has an important property: its path groupoid is a so-called action groupoid of that group corresponding to the regular action. We can then consider actions beyond the regular action, yielding the notion of an action quiver.
There are two important consequences of the ideas in this section: firstly, we obtain a dictionary to translate between the language of quiver geometry and group theory when dealing with Cayley quivers, and secondly, we can see in what exact sense quiver geometry can take us beyond group theory, and the spaces that group theory can describe.
Group actions #
A right group action \( \action{A} \) is the binding of a group \( \group{G} \) to an object \( \sym{X} \) on which it acts, expressed as a two-argument map \( \functionSignature{\function{\action{A}}}{\TuFo{\sym{X}, \group{G}}}{\sym{X}} \) that encodes how elements of \( \group{G} \) effect elements of \( \sym{X} \). By fixing the second argument of the map \( \action{A} \) we obtain a family of maps \( \setConstructor{\functionSignature{\function{\action{A}_{\groupElement{g}}}}{\sym{X}}{\sym{X}}}{\elemOf{\groupElement{g}}{\group{G}}} \), called Cayley functions. It is these maps that encode the behavior of the group \( \group{G} \), with function composition playing the role of group multiplication.
An action must have the property that we can compose two elements of the group and then act with the result, and this is the same as acting with the individual elements in sequence:
\[ \function{\action{A}_{\groupElement{g}\iGmult \groupElement{h}}}(\sym{x}) = \function{\action{A}_{\groupElement{h}}}(\function{\action{A}_{\groupElement{g}}}(\sym{x})) \]Note that we will work only with right actions, as defined above, as these will look more natural for our applications, although left actions are more common in other literature. The condition for a left action is similar but the functions \( \action{A}_{\groupElement{h}} \) and \( \action{A}_{\groupElement{g}} \) in the above condition are applied in the opposite order.
A final and obvious requirement is that the identity element of the group should leave \( \sym{X} \) unchanged:
\[ \function{\action{A}_{\groupElement{e}}}(\sym{x}) = \sym{x} \]Self actions #
Perhaps the most natural group action of \( \group{G} \) is given by the self action, in which we allow a group to act on itself, so that the \( \group{G} \)-set is \( \group{G} \) itself: \( \sym{X} = \group{G} \). The action is defined by \( \mto{\TuFo{\groupoidElement{x}, \groupElement{g}}}{\groupElement{x}\Gmult \groupElement{g}} \). The representative of a particular group element \( \groupElement{g} \) is the function that right-multiplies by \( \groupElement{g} \):
\[ \function{\action{A}_{\groupElement{g}}}\defEqualSymbol \mto{\groupElement{x}}{\groupElement{x}\Gmult \groupElement{g}} \]This action is faithful, meaning that it fully captures the behavior of the original group. We can state this formally in terms of the curried form of \( \function{A} \), which is then an injective group homomorphism \( \functionSignature{\function{\action{A}}}{\group{G}}{\symmetricGroup{\group{G}}} \). The famous Cayley's theorem states that \( \group{G} \) is isomorphic to its image under \( \function{A} \): we have "embedded" \( \group{G} \) into the group of permutations of its elements. Any action that is equivalent to the self-action (under relabelling of elements of the \( \group{G} \)-set) is known as a regular action.
For brevity we'll sometimes write the self action of \( \group{G} \) as \( \selfAction{\group{G}} \).
Action groupoids #
With these terms defined, we can now define the action groupoid of a particular group action \( \action{A} \). We'll write this groupoid as \( \actionGroupoid{\action{A}} \). The elements of \( \actionGroupoid{\action{A}} \) are given below:
\[ \actionGroupoid{\action{A}}\defEqualSymbol \setConstructor{\TuFo{\sym{x}, \groupElement{g}, \sym{y}}}{\sym{y} = \function{\action{A}_{\groupElement{g}}}(\sym{x}),\;\elemOf{\sym{x},\sym{y}}{\sym{X}},\;\elemOf{\groupElement{g}}{\group{G}}} \]In other words, the elements of \( \actionGroupoid{\action{A}} \) are "acts": an element \( \elemOf{\sym{x}}{\sym{X}} \), a choice of \( \elemOf{\groupElement{g}}{\group{G}} \), and its image under \( \action{A}_{\groupElement{g}} \).
We can see \( \actionGroupoid{\action{A}} \) as encoding a family of relations \( \actionGroupoid{\action{A}}_{\groupElement{g}} \) indexed by \( \group{G} \):
\[ \actionGroupoid{\action{A}}_{\groupElement{g}}\defEqualSymbol \setConstructor{\TuFo{\sym{x}, \sym{y}}}{\sym{y} = \function{\action{A}_{\groupElement{g}}}(\sym{x}),\;\elemOf{\sym{x},\sym{y}}{\sym{X}}} \]To use a database analogy, we have “grouped by” the 2’nd element of each 3-tuple to obtain this indexed family, and this retains the same information:
\[ \actionGroupoid{\action{A}}\isomorphicSymbol \paren{\mto{\groupElement{g}}{\actionGroupoid{\action{A}}_{\groupElement{g}}}} \]These relations \( \actionGroupoid{\action{A}}_{\groupElement{g}} \) are literally just the set-theoretic relations for the functions \( \action{A}_{\groupElement{g}} \), so we have done nothing very sophisticated here.
Groupoid multiplication of elements of \( \actionGroupoid{\action{A}} \) is defined as:
\[ \TuFo{\sym{x}, \groupElement{g}, \sym{y}}\gmult \TuFo{\sym{y}, \groupElement{h}, \sym{z}}\defEqualSymbol \TuFo{\sym{x}, \groupElement{g}\iGmult \groupElement{h}, \sym{z}} \]The multiplication is not defined when the first "act" ends at a different element of \( \sym{X} \) from where the second "act" begins (\( \sym{y} \neq \primed{\sym{y}} \)):
\[ \TuFo{\sym{x}, \groupElement{g}, \sym{y}}\gmult \TuFo{\primed{\sym{y}}, \groupElement{h}, \sym{z}}\defEqualSymbol \nullElement \]Action quiver #
Examples: Sym(3) #
Consider the symmetric group \( \symmetricGroup{3} \) acting on the list \( \list{\reFo{\fiSqToSy},\grFo{\fiSqToSy},\blFo{\fiSqToSy}} \). Let's visualize the action quiver, where we choose as generators of the group the transpositions \( \transposition{1}{2} \) and \( \transposition{2}{3} \) to be our cardinals:
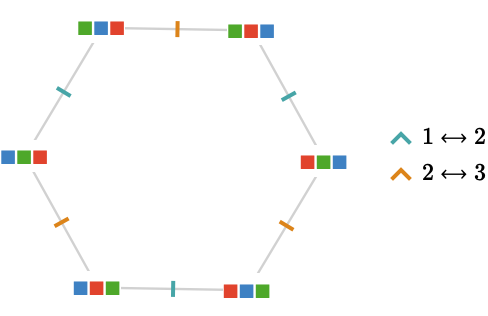
This is isomorphic to the Cayley quiver of \( \symmetricGroup{3} \).
But we can also act on a list that contains two indistinguishable elements, for example, \( \list{\reFo{\fiSqToSy},\reFo{\fiSqToSy},\blFo{\fiSqToSy}} \):
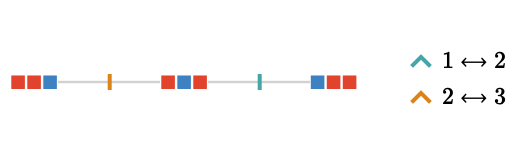
Effectively we have glued together the vertices of the Cayley quiver in which the green and red elements occur in the same pattern of positions. This is no longer a Cayley quiver for any group. This can easily be deduced because it is not transitive: the end vertices have degree 1, and the central vertex degree 2.
Examples: Sym(4) #
Let us repeat this idea for \( \symmetricGroup{4} \), first acting on the set \( \list{\reFo{\fiSqToSy},\grFo{\fiSqToSy},\blFo{\fiSqToSy},\daGFo{\fiSqToSy}} \) via generators \( \transposition{1}{2},\transposition{2}{3},\transposition{3}{4} \):
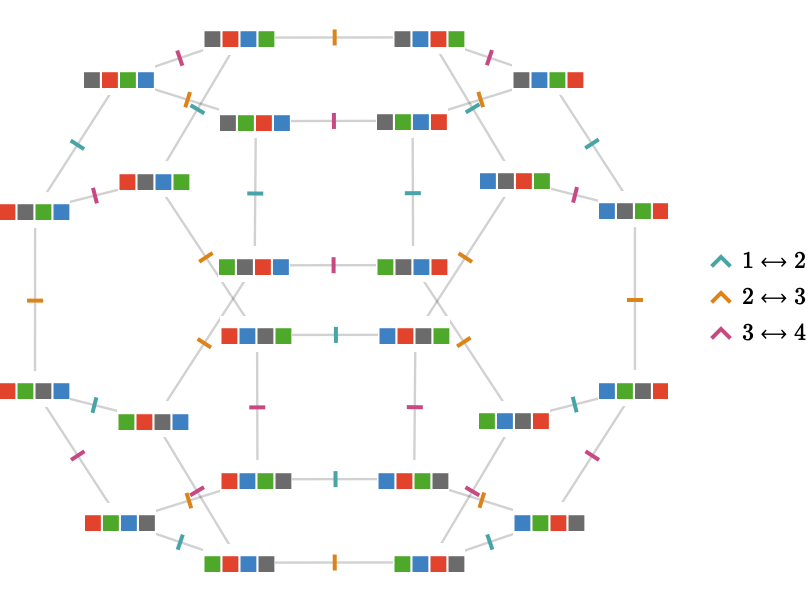
You might notice that we have obtained the edge graph of the truncated octahedron:
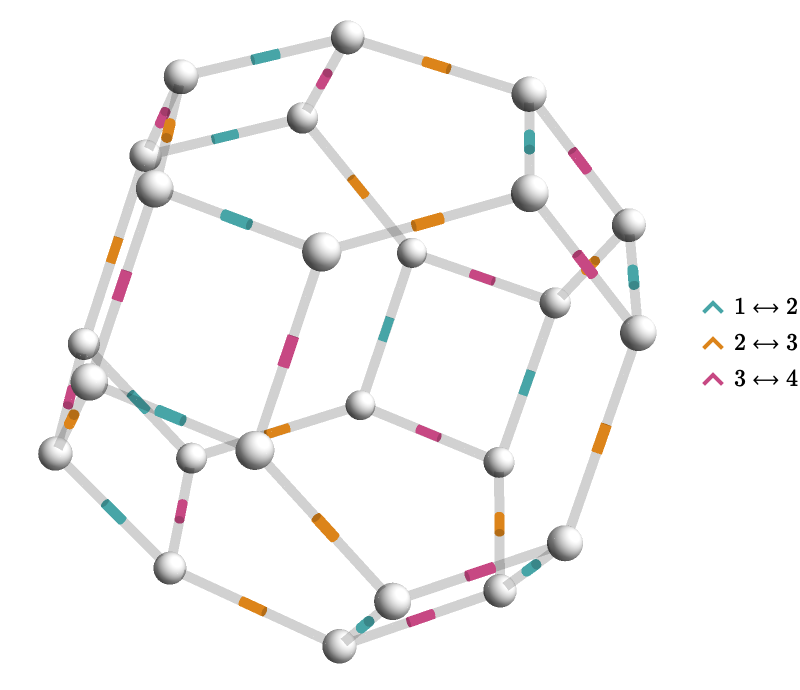
This kind of object is known as a permutohedron.
We will now allow \( \symmetricGroup{4} \) to act on a list with only three distinct elements \( \list{\reFo{\fiSqToSy},\reFo{\fiSqToSy},\grFo{\fiSqToSy},\blFo{\fiSqToSy}} \):
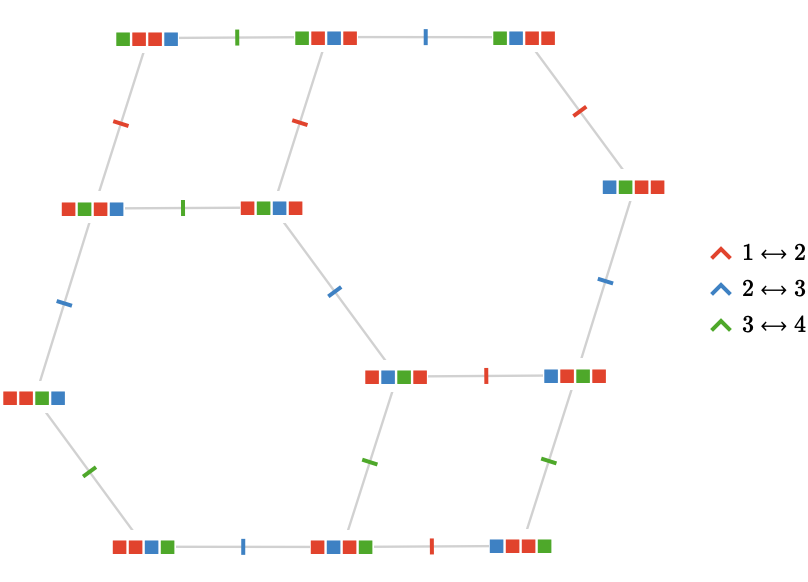
Again we obtain a quiver that is not a Cayley quiver.
Lastly, we can act on a set with only two distinct elements \( \list{\reFo{\fiSqToSy},\reFo{\fiSqToSy},\blFo{\fiSqToSy},\blFo{\fiSqToSy}} \):
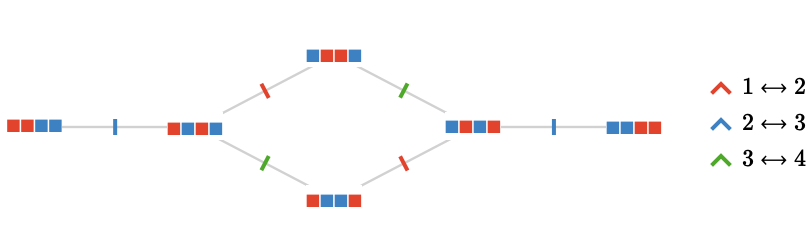
Action quiver #
In all of these examples, we have constructed particular actions of the symmetric group \( \symmetricGroup{\sym{n}} \) with the choice of generators given by the transpositions \( \transposition{1}{2},\transposition{2}{3},\elSy,\transposition{\paren{\sym{n} - 1}}{\sym{n}} \). We now formalize this construction.
Recall from Cayley quivers that the Cayley quiver \( \bindCayleyQuiver{\group{G}}{\sym{J}} \) for group \( \group{G} \) and set of generators \( \sym{J} = \list{\groupGenerator{j}_1,\groupGenerator{j}_2,\elSy} \) is defined as follows:
\[ \begin{aligned} \vertexList(\bindCayleyQuiver{\group{G}}{\sym{J}})&\defEqualSymbol \group{G}\\ \edgeList(\bindCayleyQuiver{\group{G}}{\sym{J}})&\defEqualSymbol \setConstructor{\tde{\groupElement{g}}{\groupElement{g}\Gmult \groupGenerator{j}}{\card{j}}}{\elemOf{\groupElement{g}}{\group{G}},\;\elemOf{\groupGenerator{j}}{\sym{J}}}\end{aligned} \]We now extend this idea to arbitrary action \( \action{A} \) on the group \( \group{G} \) over \( \group{G} \)-set \( \sym{X} \), again defined in terms of a set of generators \( \sym{J} = \list{\groupGenerator{j}_1,\groupGenerator{j}_2,\elSy} \). Associated to each \( \elemOf{\groupGenerator{j}}{\sym{J}} \) is a Cayley function \( \functionSignature{\function{\action{A}_{\groupGenerator{j}}}}{\sym{X}}{\sym{X}} \). We define the action quiver \( \bindActionQuiver{\action{A}}{\sym{J}} \) as follows:
\[ \begin{aligned} \vertexList(\bindActionQuiver{\action{A}}{\sym{J}})&\defEqualSymbol \sym{X}\\ \edgeList(\bindActionQuiver{\action{A}}{\sym{J}})&\defEqualSymbol \setConstructor{\tde{\sym{x}}{\function{\action{A}_{\groupGenerator{j}}}(\sym{x})}{\card{j}}}{\elemOf{\sym{x}}{\sym{X}},\;\elemOf{\groupGenerator{j}}{\sym{J}}}\end{aligned} \]In other words, the edges of \( \bindActionQuiver{\action{A}}{\sym{J}} \) depict "primitive acts" of \( \group{G} \) on the elements of \( \sym{X} \): those acts associated with generators \( \elemOf{\groupGenerator{j}}{\sym{J}} \).
The Cayley quiver \( \bindCayleyQuiver{\group{G}}{\sym{J}} \) is obviously an example of an action quiver \( \bindActionQuiver{\action{A}}{\sym{J}} \), specifically in which the action is the self-action \( \selfAction{\group{G}} \) of \( \group{G} \), which is now revealed to be the motivation for the notation \( \bindCayleyQuiver{\group{G}}{\sym{J}} \) in the first place!
Path vs. action groupoid #
You might notice that the groupoid multiplication in the action groupoid \( \actionGroupoid{\action{A}} \) of a group action \( \action{A} \) is very similar to the group multiplication in the path groupoid \( \pathGroupoid{\quiver{Q}} \) of a quiver \( \quiver{Q} \) that we saw in Path groupoids.
For action groupoids, we can only compose two acts when the first "ends" at a state where the second "begins":
\[ \TuFo{\sym{x}, \groupElement{g}, \sym{y}}\gmult \TuFo{\sym{y}, \groupElement{h}, \sym{z}} = \TuFo{\sym{x}, \groupElement{g}\iGmult \groupElement{h}, \sym{z}} \]For path groupoids, we can only compose two paths when the first ends at a vertex where the second begins:
\[ \pathCompose{\paren{\pathWord{\vert{x}}{\wordSymbol{V}}{\vert{y}}}}{\paren{\pathWord{\vert{y}}{\wordSymbol{W}}{\vert{z}}}} = \parenPathWord{\vert{y}}{\concat{\wordSymbol{V} \wordSymbol{W}}}{\vert{z}} \]Indeed, it is a simple but useful exercise to check that this is similarity is an groupoid isomorphism in the case where the quiver is an action quiver:
\[ \pathGroupoid{\bindActionQuiver{\action{A}}{\sym{J}}}\isomorphicSymbol \actionGroupoid{\action{A}} \]In words, acts are paths, with all acts being formed from primitive acts, which are edges (or their inverses).
Summary #
We can now state the relationship between group actions and action quivers in the following "commutative diagram" (whose formal status will have to wait until we introduce category theory at a later stage):
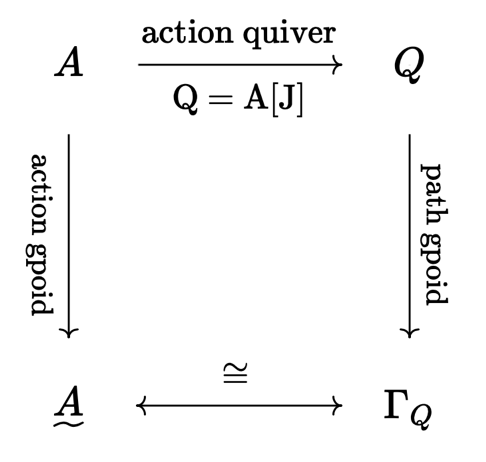
In words: when a quiver is an action quiver of group \( \group{G} \), its path groupoid coincides with action groupoid of \( \group{G} \), summarized in the motto "acts are paths".
The relationship can be specialized for the case of a Cayley quiver:
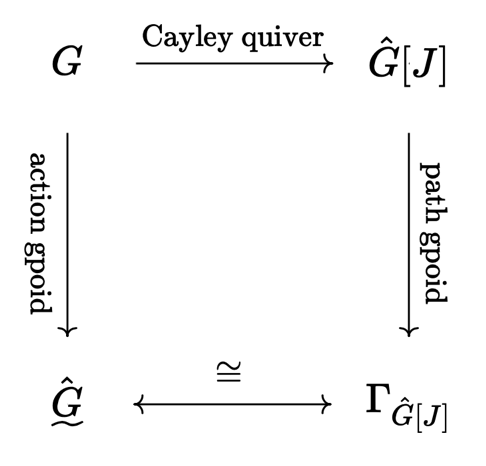
The benefit of keeping this diagram in mind is that it will allow us to interpret various constructions on quivers in terms of groups. When the quivers are transitive quivers, we will end up describing familiar mathematical constructions on groups. But crucially, for non-transitive quivers, we will find ourselves outside the domain of group theory, but with intuitions to guide us from the transitive case.