Transitive quivers #
In this short section we introduce some common families of quiver that are simple and ubiquitous in quiver geometry. Their most important property is that they obey a property called vertex transitivity, though some fine print applies to this statement that we'll get into. We will name these families, visualize them, and give some simple properties. In later sections we will see that some of them are the simplest examples of lattice quivers, generated in a particular way by smaller quivers via linear representations. We'll also see how some of them can be formed from the quiver products of others.
These families are parameterized by positive integers (and infinity).
Lattice quiver families #
The first set of families, the lattice quiver families, are parameterized by a single positive integer \( 0 \le \sym{n} \le \infty \), which in some sense measure their "linear size", which refers to the number of vertices visited by the longest possible path that consists of a single repeated cardinal. For \( \sym{n} = \infty \) we pass to the limit of an infinitely large quiver, and these are the quivers that obey vertex transitivity in the proper sense.
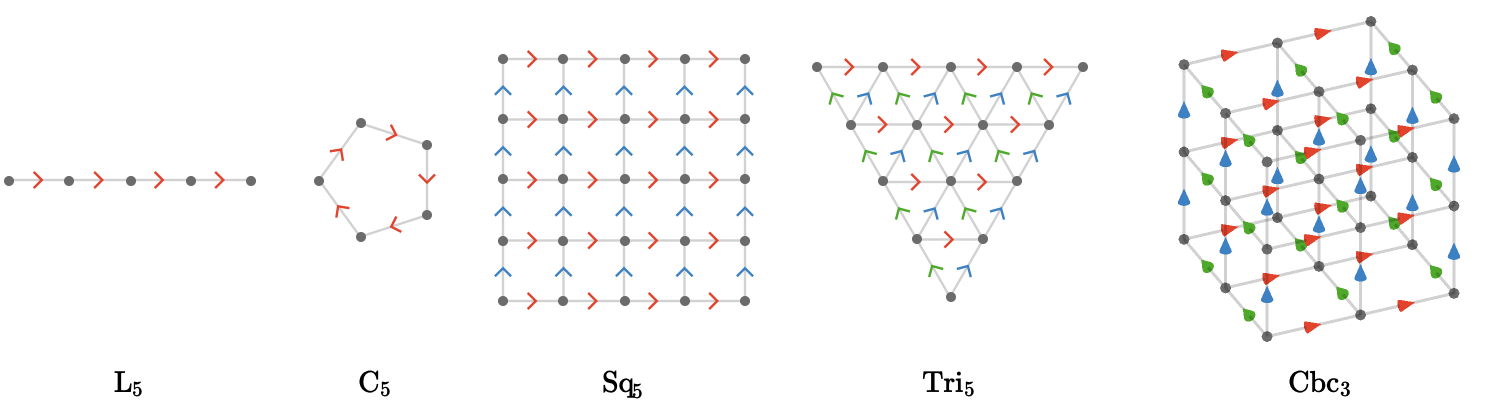
| name | symbol | cardinals | dimension |
|---|---|---|---|
| line quiver | \( \subSize{\lineQuiver }{\sym{n}} \) | 1 | 1 |
| cycle quiver | \( \subSize{\cycleQuiver }{\sym{n}} \) | 1 | 1 |
| square quiver | \( \subSize{\squareQuiver }{\sym{n}} \) | 2 | 2 |
| triangular quiver | \( \subSize{\triangularQuiver }{\sym{n}} \) | 3 | 2 |
| cubic quiver | \( \subSize{\cubicQuiver }{\sym{n}} \) | 3 | 3 |
We will elaborate on the meaning of "dimension" shortly.
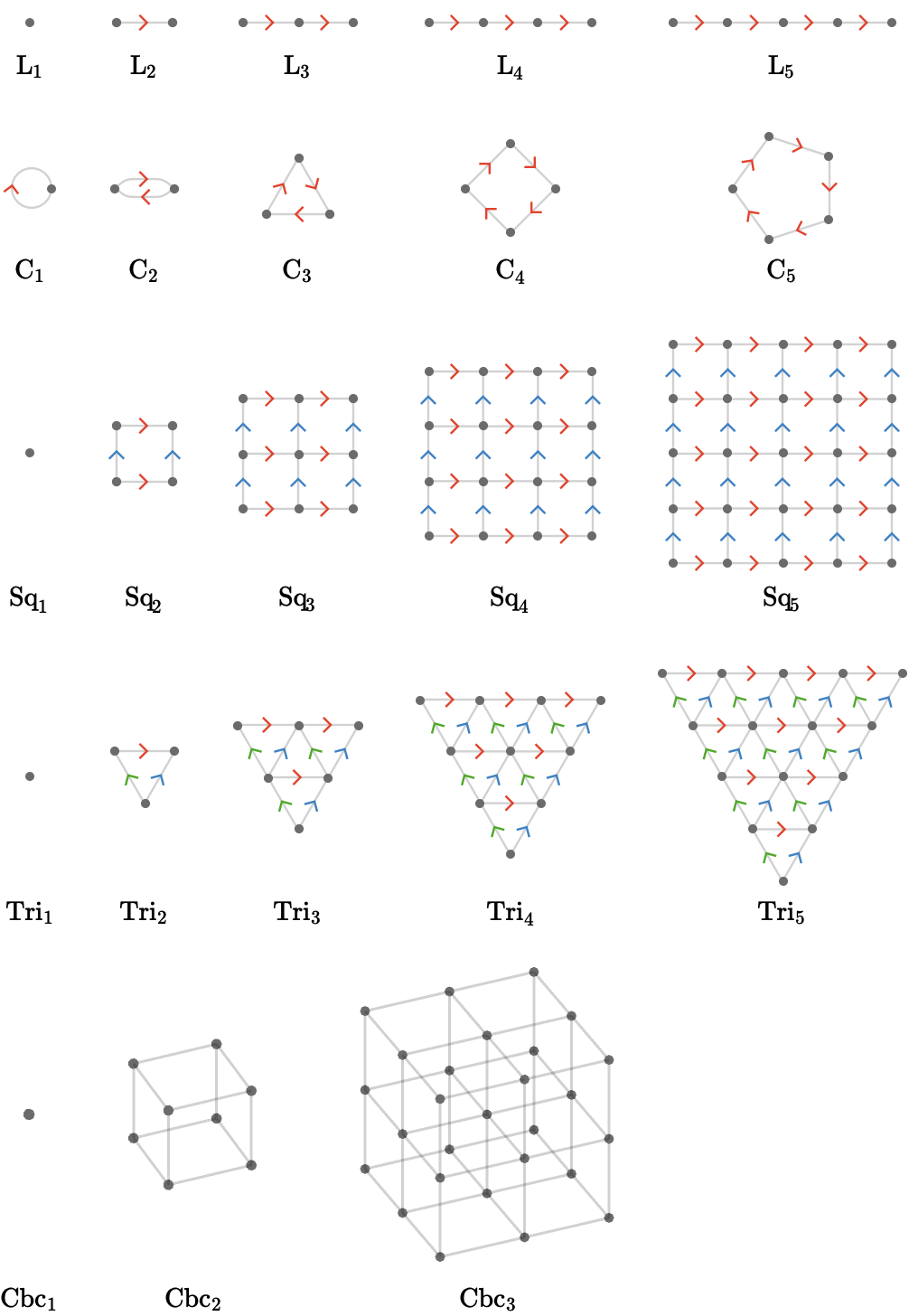
Below we show an example quiver from each family corresponding to \( \sym{n} = 5 \), except for the cubic quiver, where we show \( \sym{n} = 3 \) for size reasons:
Terminology #
We'll use the line quiver to illustrate these conventions, but the same conventions apply to the other quivers:
-
When \( \sym{n} \) is fixed at a particular finite value, e.g. \( \sym{n} = 5 \), we’ll write \( \subSize{\lineQuiver }{5} \), and refer to this in words as the 5-line quiver.
-
When \( \sym{n} \) is fixed to be merely finite, we’ll refer to e.g. a finite line quiver.
-
When \( \sym{n} \) is fixed at infinity, we’ll write \( \subSize{\lineQuiver }{ \infty } \) and refer to this in words as the infinite line quiver or just the line quiver.
As a special case, we define \( \subSize{\cycleQuiver }{ \infty } = \subSize{\lineQuiver }{ \infty } \), since we cannot form a non-empty closed finite path in \( \subSize{\cycleQuiver }{ \infty } \).
Infinite cases #
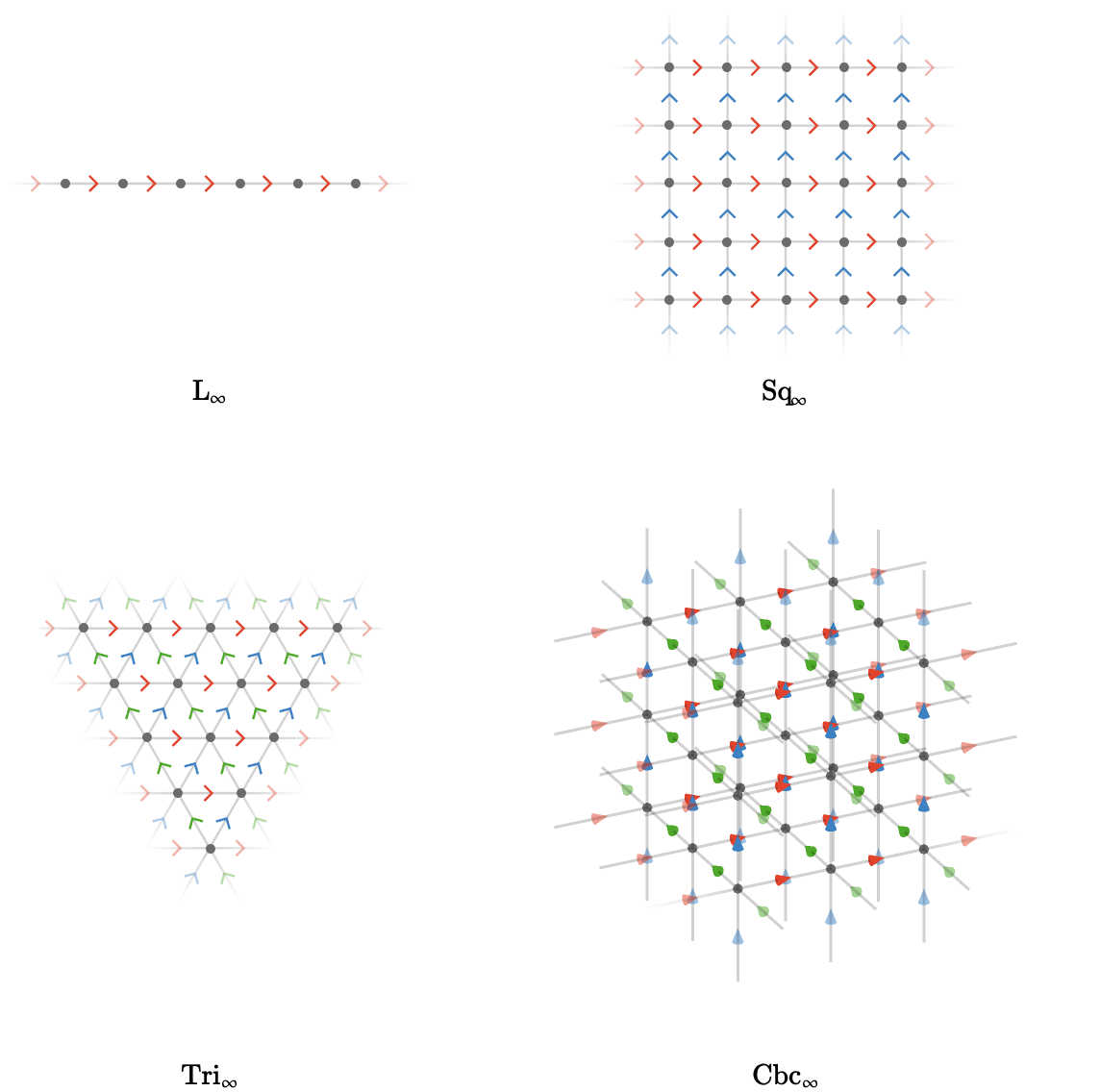
For the line, square, triangular, and grid quivers, we obtain transitive quivers only when \( \sym{n} = \infty \), since these are the only quivers for which there is no periphery. Here we show finite portions of these infinite quivers, with the boundary shown faded to indicate it is only a finite view of an infinite object:
Size #
The smallest meaningful sizes of the lattice families are shown below.
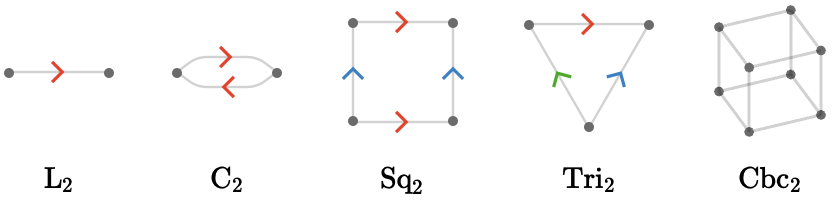
At size 1, the line, square, and triangle collapse to a single vertex with no edges, the cycle is known as 1-bouquet quiver.

Here we show a sequence of increasing size for each family:
Special quiver families #
The special families parameterize the number of cardinals with a parameter \( \sym{k} \)*.* The three special families are:
| name | symbol | cardinals | dimension |
|---|---|---|---|
| bouquet quiver | \( \bouquetQuiver{\sym{k}} \) | \( \sym{k} \) | \( 0 \) |
| grid quiver | \( \subSize{\gridQuiver{\sym{k}}}{\sym{n}} \) | \( \sym{k} \) | \( \sym{k} \) |
| tree quiver | \( \subSize{\treeQuiver{\sym{k}}}{\sym{n}} \) | \( \sym{k} \) | \( \infty \) |
The tree quiver is only defined for odd \( \sym{n} \).
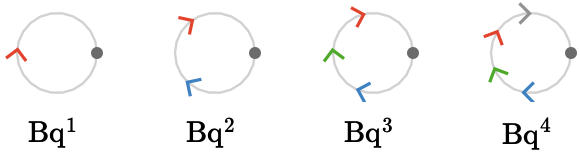
Bouquet quiver #
We visualize the bouquet quiver \( \bouquetQuiver{\sym{k}} \) for \( \elemOf{\sym{k}}{\oneTo{4}} \):
Grid quiver #
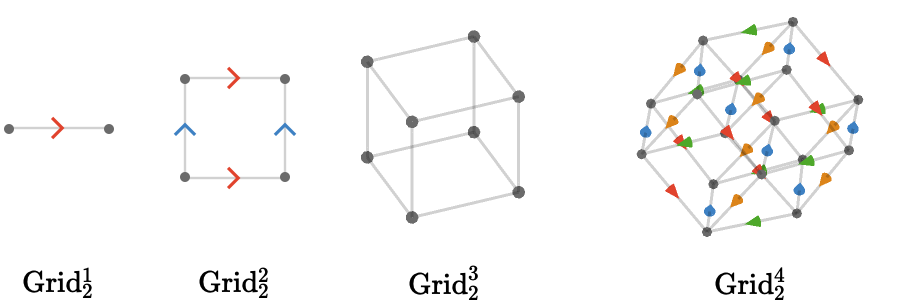
The grid quiver \( \subSize{\gridQuiver{\sym{k}}}{\sym{n}} \) generalizes the sequence \( \subSize{\lineQuiver }{\sym{n}},\subSize{\squareQuiver }{\sym{n}},\subSize{\cubicQuiver }{\sym{n}},\elSy \) to an arbitrary number of cardinals \( \sym{k} \).
We visualize the grid quiver \( \subSize{\gridQuiver{\sym{k}}}{\sym{n}} \) for \( \elemOf{\sym{k}}{\oneTo{3}} \), fixing \( \sym{n} = 2 \):
Tree quiver #
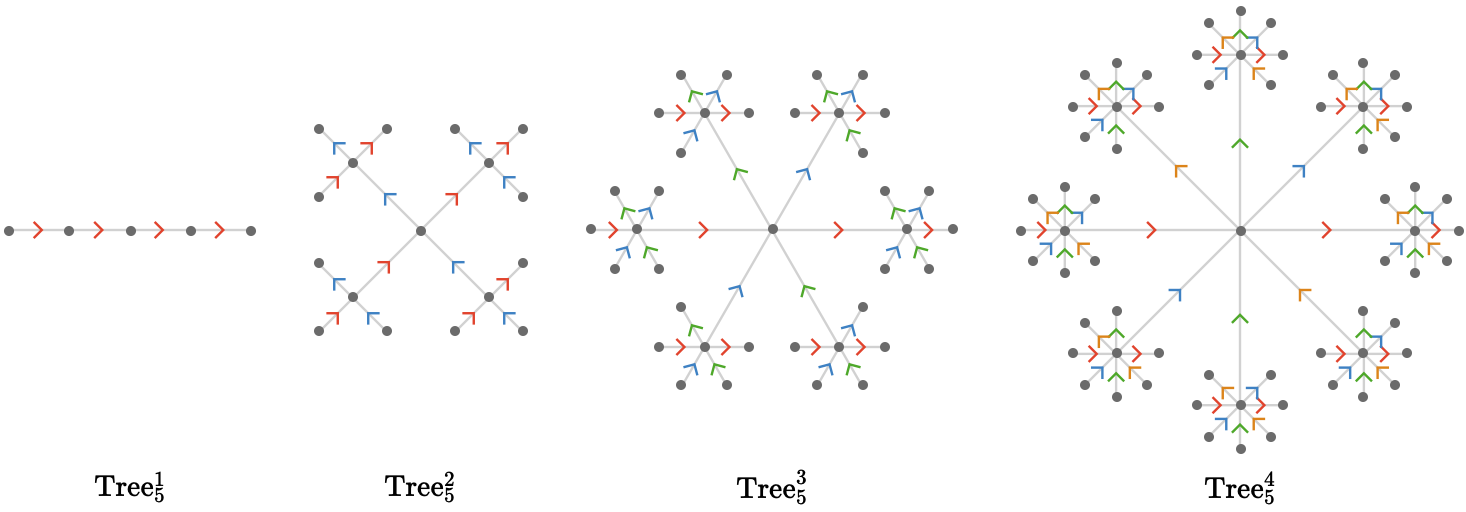
The tree quiver \( \subSize{\treeQuiver{\sym{k}}}{\sym{n}} \) is the "freest possible quiver" on \( \sym{k} \) cardinals, in the sense that every possible path one can form from these cardinals will reach a distinct vertex.
We fix \( \sym{n} = 5 \), visualizing the tree quiver \( \subSize{\treeQuiver{\sym{k}}}{5} \) for \( \elemOf{\sym{k}}{\oneTo{4}} \):
We now fix \( \sym{k} = 2 \), visualizing \( \subSize{\treeQuiver{2}}{\sym{n}} \) for \( \elemOf{\sym{n}}{\list{1,3,5,7,9}} \):
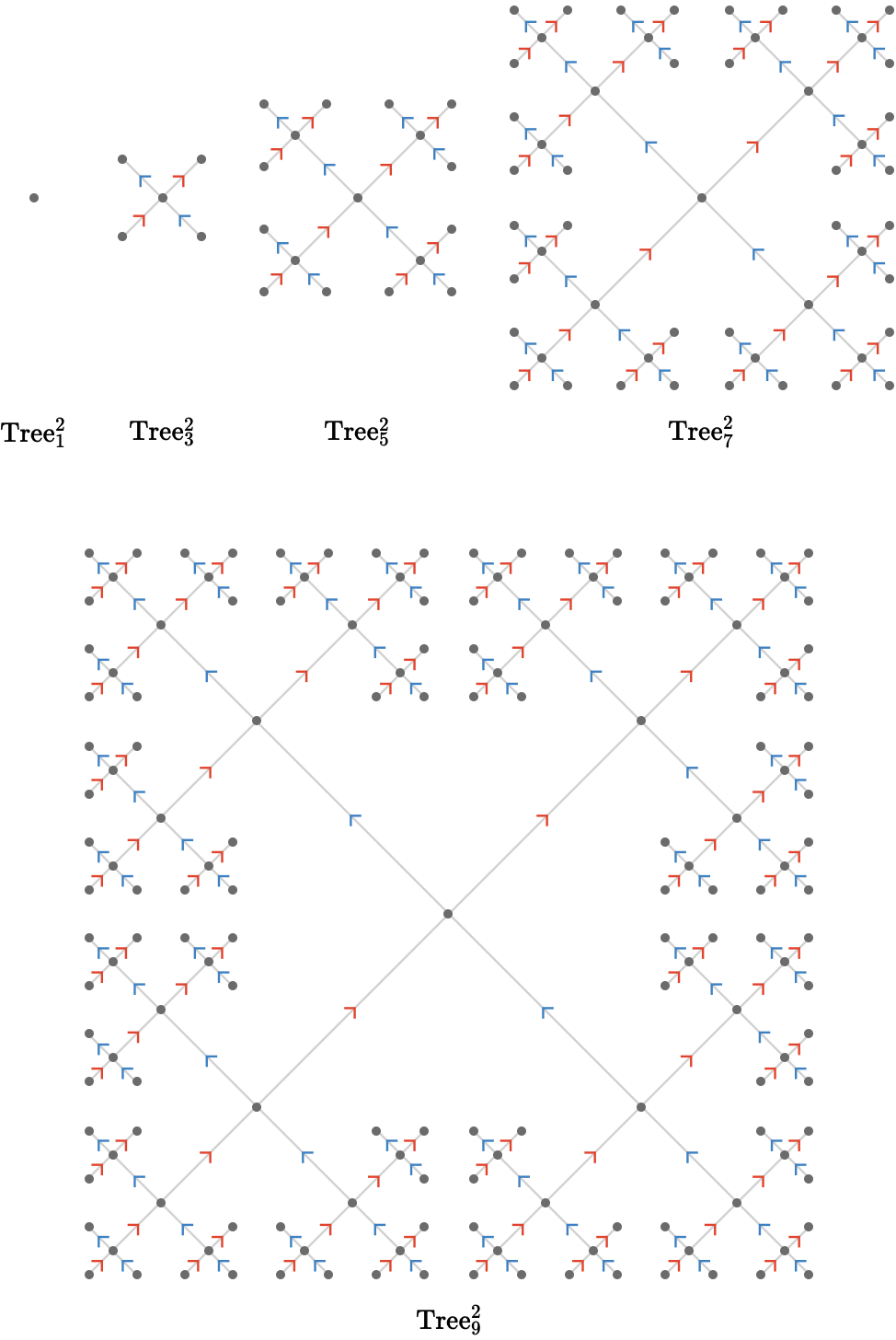
Lastly, we fix \( \sym{k} = 3 \), visualizing \( \subSize{\treeQuiver{3}}{\sym{n}} \) for \( \elemOf{\sym{n}}{\list{1,3,5,7}} \):
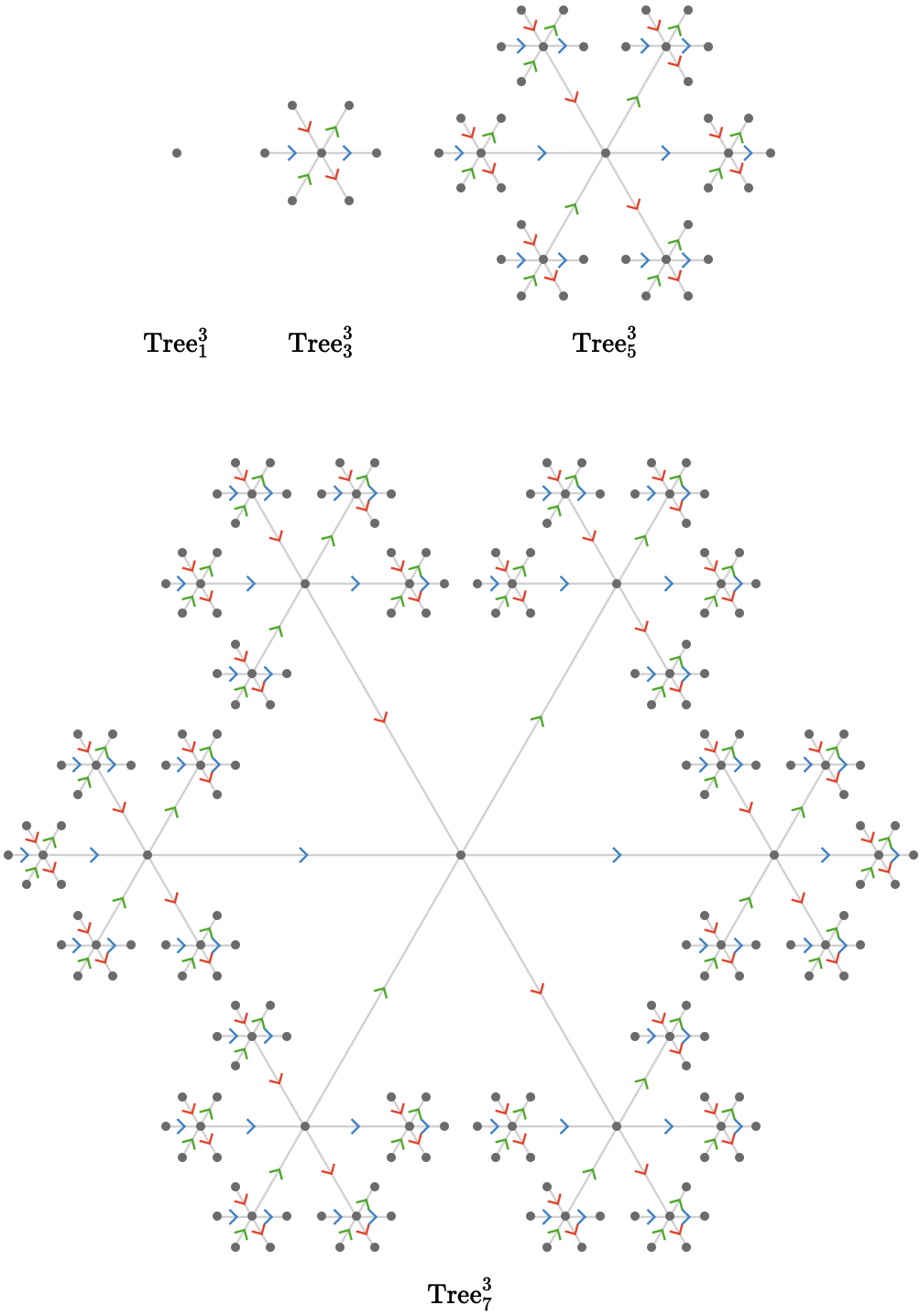
Cardinals #
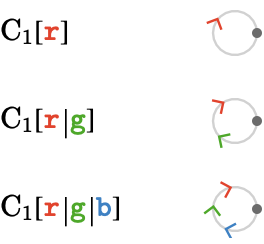
When we wish to be explicit about the cardinals present in these quivers, we will use square bracket notation, e.g. \( \bindCards{\subSize{\triangularQuiver }{\sym{n}}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \), to indicate the names of the cardinals present in the quiver. We'll refer to this in English as "the triangle quiver on \( \reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}} \)".
The one-dimensional quivers, the line and cycle quiver, both have only one cardinal:
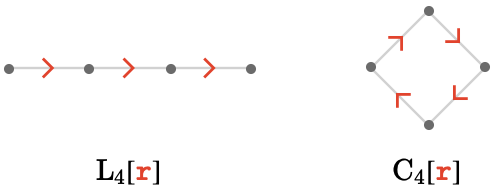
The square quiver has two cardinals:

The triangular and cubic quivers have three cardinals:
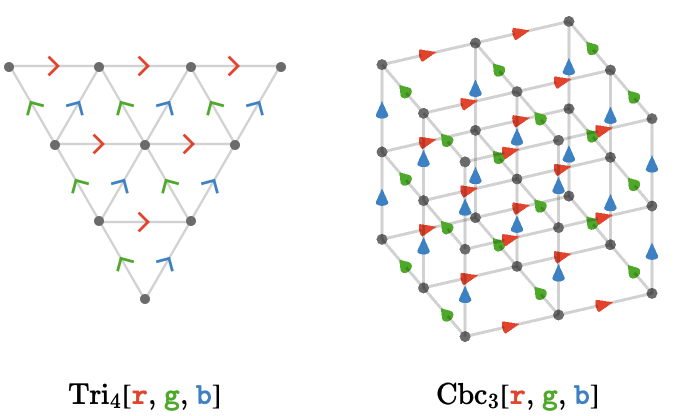
Per-cardinal dimensions #
We can form a "rectangular" square quiver by specifying different dimensions for the different cardinals. We'll use the notation \( \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \sym{w},\blFo{\card{b}}\compactBindingRuleSymbol \sym{h}} \) in this case. Here is a rectangular square quiver \( \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol 5,\blFo{\card{b}}\compactBindingRuleSymbol 3} \):
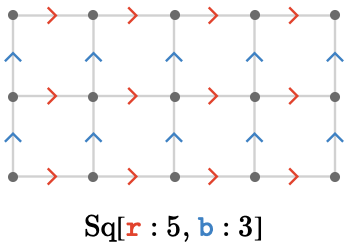
When the symbols of the cardinals are not relevant, we will just refer to this quiver as \( \bindCardSize{\squareQuiver }{\sym{w},\sym{h}} \).
Transitivity #
A quiver is transitive if its vertices all look the same, or equivalently, that no vertex is special. We will have to develop the path groupoid to define this more precisely, but for now we can understand this property as implying the condition that all vertices have the same degree (number of incident edges), and the same cardinals available to them.
This condition is not sufficient to ensure a quiver is transitive, but it is necessary. Again, we'll have to wait for a more precise definition.
The quivers we consider here are all transitive in this sense, but typically only when we consider their infinite versions. \( \subSize{\lineQuiver }{3} \) for example, has a "middle" vertex and two "end vertices": all have different cardinals available to them. \( \subSize{\lineQuiver }{ \infty } \), in contrast, has no special vertices at all. The only exception to this pattern is \( \subSize{\cycleQuiver }{\sym{n}} \), which is transitive for any \( \sym{n} \).
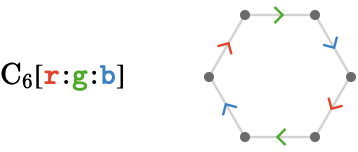
As an example of an intransitive lattice, consider the hexagonal quiver (which we will define formally in a later section):
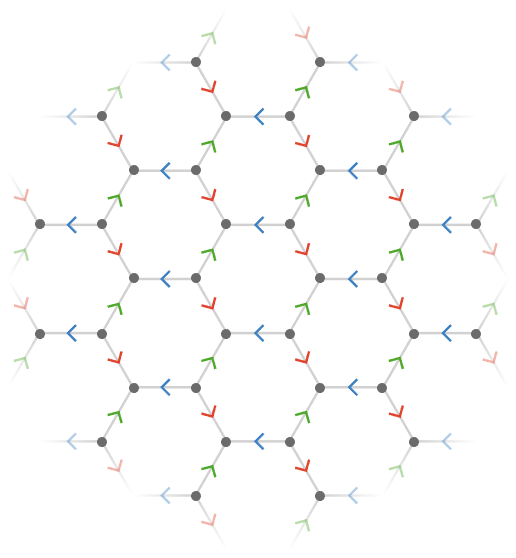
Although all vertices have degree 3, the vertices consist of two types: the "inward" vertices with incident cardinals \( \list{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \), and the "outward" vertices with incident cardinals \( \list{\reFo{\inverted{\card{r}}},\grFo{\inverted{\card{g}}},\blFo{\inverted{\card{b}}}} \). We will examine these more general quivers in the section Intransitive lattices.
Vertex and edge counts #
The number of vertices and edges as a function of the size is shown in a table below:
| quiver | # vertices | # edges |
|---|---|---|
| \( \bouquetQuiver{\sym{k}} \) | \( 1 \) | \( \sym{k} \) |
| \( \subSize{\lineQuiver }{\sym{n}} \) | \( \sym{n} \) | \( \sym{n} - 1 \) |
| \( \subSize{\cycleQuiver }{\sym{n}} \) | \( \sym{n} \) | \( \sym{n} \) |
| \( \subSize{\squareQuiver }{\sym{n}} \) | \( \power{\sym{n}}{2} \) | \( 2 \, \sym{n} \, \paren{\sym{n} - 1} \) |
| \( \subSize{\triangularQuiver }{\sym{n}} \) | \( \frac{1}{2} \, \sym{n} \, \paren{\sym{n} + 1} \) | \( \frac{3}{2} \, \sym{n} \, \paren{\sym{n} - 1} \) |
| \( \subSize{\cubicQuiver }{\sym{n}} \) | \( \power{\sym{n}}{3} \) | \( 3 \, \power{\sym{n}}{2} \, \paren{\sym{n} - 1} \) |
| \( \subSize{\gridQuiver{\sym{k}}}{\sym{n}} \) | \( \power{\sym{n}}{\sym{k}} \) | \( \sym{k} \, \power{\sym{n}}{\sym{k} - 1} \, \paren{\sym{n} - 1} \) |
| \( \subSize{\treeQuiver{\sym{k}}}{2 \, \sym{n} + 1} \) | \( \frac{\sym{k} \, \power{\paren{2 \, \sym{k} - 1}}{\sym{n}} - 1}{\sym{k} - 1} \) | \( \frac{\sym{k} \, \paren{\power{\paren{2 \, \sym{k} - 1}}{\sym{n}} - 1}}{\sym{k} - 1} \) |
Dimension #
To define the dimension of a particular infinite family of quivers, we can look at the number of vertices that can be reached from any origin vertex as a function of the number of edges we are allowed to traverse.
Here we illustrate this idea for the line, square, and triangular, and cubic quivers:
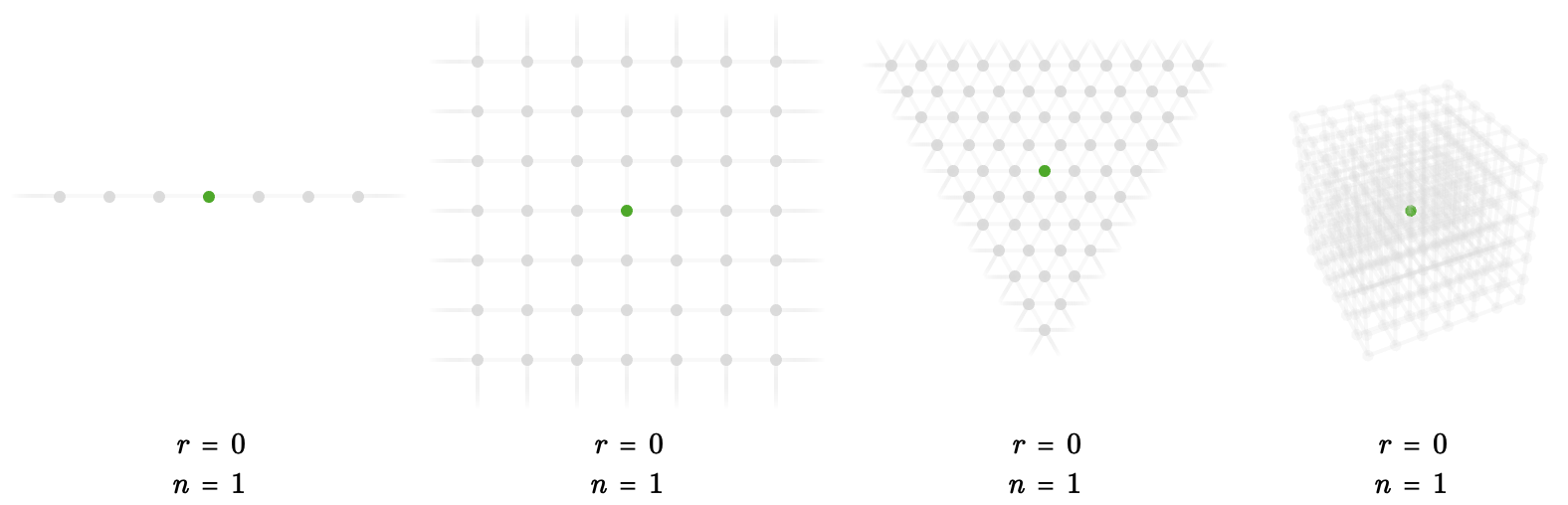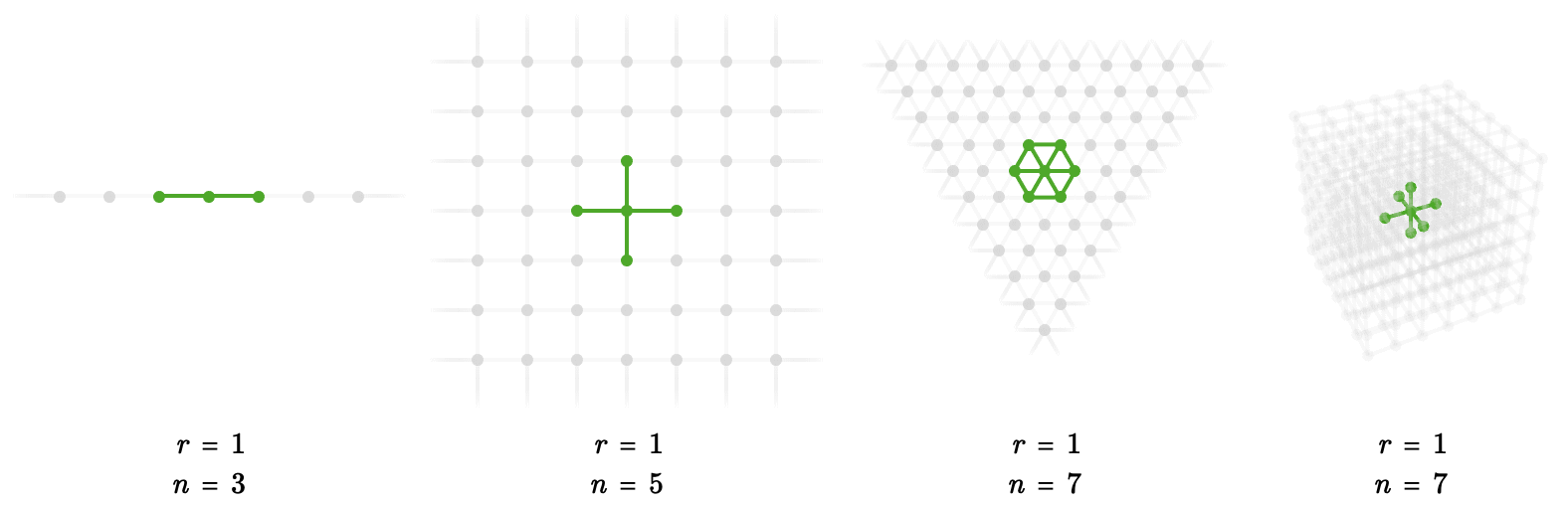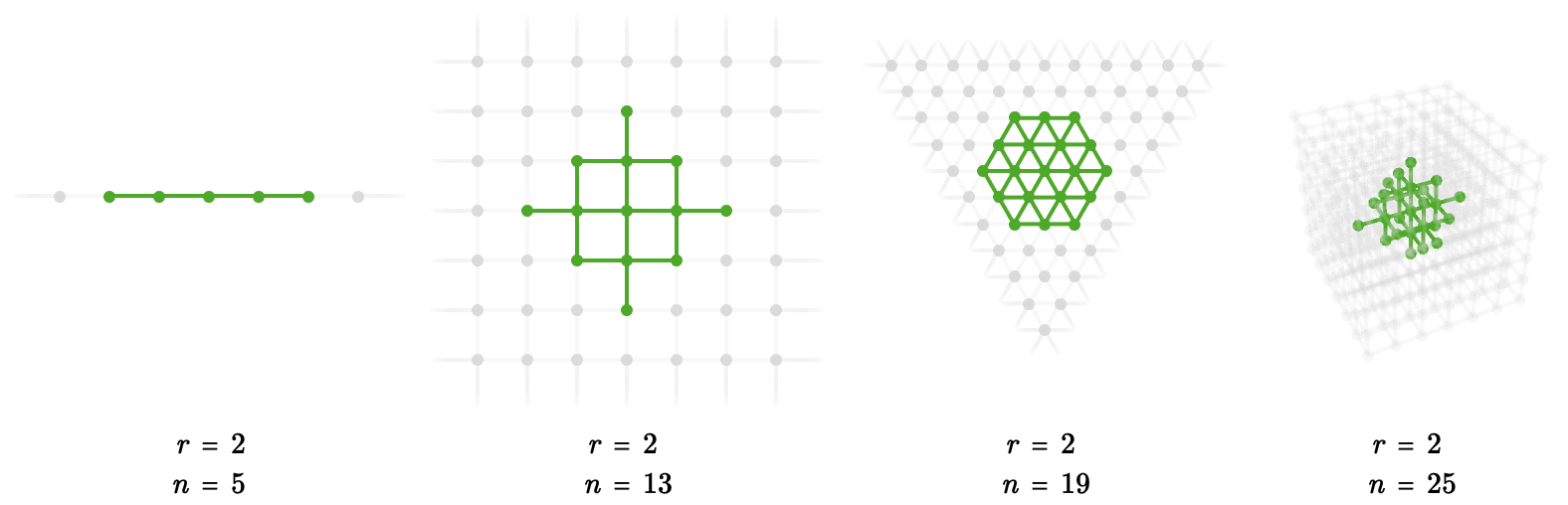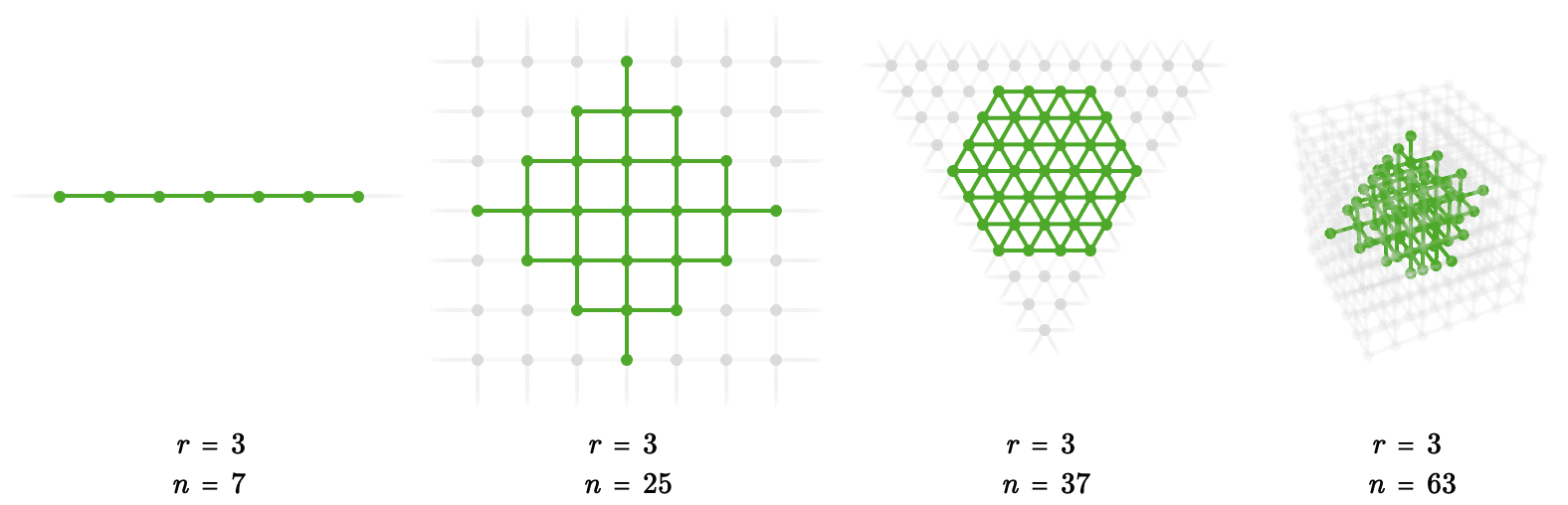
The number of vertices in such a discrete ball of radius \( \sym{r} \) is given by the following table:
| quiver | #ball vertices | leading term | dimension |
|---|---|---|---|
| \( \bouquetQuiver{\sym{k}} \) | \( 1 \) | \( 1 \) | \( 0 \) |
| \( \subSize{\lineQuiver }{ \infty } \) | \( \poly{2 \, \sym{r} - 3} \) | \( \sym{r} \) | \( 1 \) |
| \( \subSize{\cycleQuiver }{\sym{n}} \) | \( \min(\poly{2 \, \sym{r} - 3},\sym{n}) \) | \( \sym{r} \) | \( 1 \) |
| \( \subSize{\squareQuiver }{ \infty } \) | \( \poly{2 \, \sym{r} \, \paren{\sym{r} \, -1} + 1} \) | \( \power{\sym{r}}{2} \) | \( 2 \) |
| \( \subSize{\triangularQuiver }{ \infty } \) | \( \poly{3 \, \sym{r} \, \paren{\sym{r} \, -1} + 1} \) | \( \power{\sym{r}}{2} \) | \( 2 \) |
| \( \subSize{\cubicQuiver }{ \infty } \) | \( \poly{2 / 3 \, \sym{r} \, \paren{\sym{r} \, \paren{2 \, \sym{r} - 3} + 4} - 1} \) | \( \power{\sym{r}}{3} \) | \( 3 \) |
| \( \treeQuiver{\sym{k}} \) | \( \frac{\sym{k} \, \power{\paren{2 \, \sym{k} - 1}}{\sym{r} - 1} - 1}{\sym{k} - 1} \) | \( \noApSy \) | \( \infty \) |
We now see the justification for the dimensions we listed before: a transitive quiver has dimension \( \sym{d} \) if it the number of vertices in a radius-\( \sym{r} \) ball scales as \( \power{\sym{r}}{\sym{d}} \). The tree quiver \( \treeQuiver{\sym{k}} \) involves a term \( \power{\paren{2 \, \sym{k} - 1}}{\sym{r} - 1} \), hence its Taylor expansion has non-zero terms of all degrees in \( \sym{r} \), and we say it has infinite dimension.
Enriched cardinal structure #
We will at times wish to "enrich" the cardinal structure of the line and cycle quivers.
Serial cardinals #
The first kind of enrichment is serial: instead of employing a single cardinal \( \card{c} \), we employ a series of cardinals \( \card{c}_1,\card{c}_2,\elSy,\card{c}_{\sym{m}} \) that is taken in alternation. We'll write this as \( \card{\card{c}_1}\serialCardSymbol \card{\card{c}_2}\serialCardSymbol \elSy\serialCardSymbol \card{\card{c}_{\sym{m}}} \).
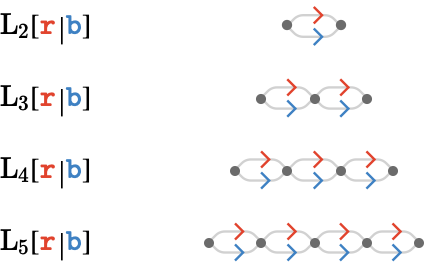
Let's take for example \( \bindCards{\subSize{\lineQuiver }{\sym{n}}}{\reFo{\card{r}}\serialCardSymbol \blFo{\card{b}}} \), which we'll refer to in English as "the 2-line quiver on \( \reFo{\card{r}} \) then \( \blFo{\card{b}} \)".
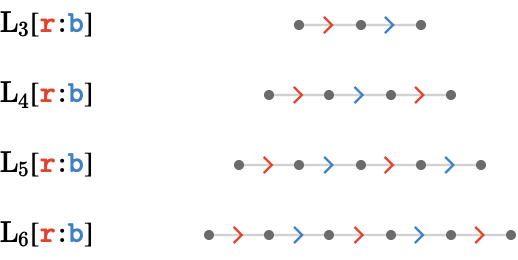
Here we have a series of 3 cardinals:

The same construction works as you would expect for the cycle quiver:
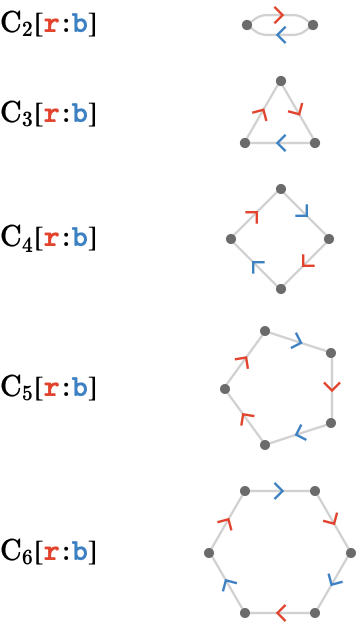
For a series of 3 cardinals:
Parallel cardinals #
The second kind of enrichment is parallel: in place of a single cardinal \( \card{c} \) we use a set of cardinals \( \card{c}_1,\card{c}_2,\elSy,\card{c}_{\sym{m}} \), all present on the same edge. We write this as \( \card{\card{c}_1}\parallelCardSymbol \card{\card{c}_2}\parallelCardSymbol \elSy\parallelCardSymbol \card{\card{c}_{\sym{m}}} \).
Here we show \( \bindCards{\subSize{\lineQuiver }{\sym{n}}}{\reFo{\card{r}}\parallelCardSymbol \blFo{\card{b}}} \), which we'll refer to in English as "the 2-line quiver on \( \reFo{\card{r}}\parallelCardSymbol \blFo{\card{b}} \)".
We can also use the multi-arrowhead convention, in which case e.g. \( \bindCards{\subSize{\lineQuiver }{3}}{\reFo{\card{r}}\parallelCardSymbol \blFo{\card{b}}} \) looks like:

Again, an important application is to put a cardinal in parallel with its inverse:

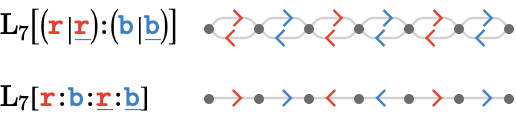
However, this violates the local uniqueness property for \( \sym{n}>2 \):

We can however combine the parallel and serial enrichments to sidestep this limitation. There are two obvious ways to do this:
The situation with the cycle quiver is similar. However, we cannot form \( \bindCards{\subSize{\cycleQuiver }{\sym{n}}}{\reFo{\card{r}}\parallelCardSymbol \reFo{\inverted{\card{r}}}} \) for any \( \sym{n} \).
We can however form \( \bindCards{\subSize{\cycleQuiver }{1}}{\reFo{\card{r}}},\bindCards{\subSize{\cycleQuiver }{1}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}},\bindCards{\subSize{\cycleQuiver }{1}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}\parallelCardSymbol \blFo{\card{b}}},\elSy \) etc., obtaining the bouquet quivers: