Cayley quivers #
Introduction #
In Transitive quivers we defined families of transitive quivers like the line, square, and triangular quivers. We now define how to obtain a Cayley quiver from a group by choosing a set of generators, or equivalently by choosing a presentation for a group. We explain how the simple transitive quivers are generated this way from \( \group{\power{\group{\mathbb{Z}}}{\sym{n}}} \).
Groups #
We briefly recall the definition of a group and some related ideas for readers who need a very short refresher:
Definition #
A group is a structure \( \TuFo{\group{G}, \Gmult } \) consisting of a set of elements \( \group{G} \) and a group multiplication (or group operation) \( \functionSignature{\function{\Gmult }}{\TuFo{\group{G}, \group{G}}}{\group{G}} \).
The multiplication is associative, so \( \groupElement{f}\Gmult \paren{\groupElement{g}\Gmult \groupElement{h}} = \paren{\groupElement{f}\Gmult \groupElement{g}}\Gmult \groupElement{h} \) for all \( \elemOf{\groupElement{f},\groupElement{g},\groupElement{h}}{\group{G}} \).
Each element \( \groupElement{g} \) also has an inverse \( \groupInverse{\groupElement{g}} \) satisfying \( \groupInverse{\groupElement{g}}\Gmult \groupElement{g} = \groupElement{g}\Gmult \groupInverse{\groupElement{g}} = \groupIdentity{e} \), where \( \groupIdentity{e}\Gmult \groupElement{g} = \groupElement{g}\Gmult \groupIdentity{e} = \group{G} \) defines the identity or unit element \( \elemOf{\groupIdentity{e}}{\group{G}} \).
We will sometimes drop the symbol \( \Gmult \) and write \( \groupElement{g}\Gmult \groupElement{h} \) as simply \( \groupElement{g}\iGmult \groupElement{h} \).
Commutators #
The commutator of two group elements is defined as follows:
\[ \groupCommutator{\groupElement{g}}{\groupElement{h}}\defEqualSymbol \groupElement{g}\iGmult \groupElement{h}\iGmult \groupInverse{\groupElement{g}}\iGmult \groupInverse{\groupElement{h}} \]Generators #
A set of generators of a group \( \list{\groupGenerator{g_1},\groupGenerator{g_2},\elSy,\groupGenerator{g_{\sym{n}}}} \) is a set of elements such that every other element of a group can be expressed as a product of the generators or their inverses.
Group words #
A group word over a set of generators is a product of generators or their inverses: an expression of the form \( \groupElement{\groupElement{h}_1}\iGmult \groupElement{\groupElement{h}_2}\iGmult \elSy\iGmult \groupElement{\groupElement{h}_{\sym{m}}} \), where each \( \elemOf{\groupElement{h}_{\sym{i}}}{\list{\groupGenerator{g_1},\groupInverse{\groupGenerator{g_1}},\elSy,\groupGenerator{g_{\sym{n}}},\groupInverse{\groupGenerator{g_{\sym{n}}}}}} \). We can combine neighboring generators when they are the same, expressing the word as a sequence (of some length smaller length \( \sym{m} \)) of integer powers \( \sym{p}_{\sym{j}} \) of generators \( \groupGenerator{g_{\sym{i}_{\sym{j}}}} \).
\[ \groupPower{\groupGenerator{g_{\sym{i}_1}}}{\sym{p}_1}\iGmult \groupPower{\groupGenerator{g_{\sym{i}_2}}}{\sym{p}_2}\iGmult \elSy\iGmult \groupPower{\groupGenerator{g_{\sym{i}_{\sym{m}}}}}{\sym{p}_{\sym{m}}}\quad \elemOf{\sym{i}_{\sym{j}}}{\oneTo{\sym{n}}},\;\elemOf{\sym{p}_{\sym{j}}}{\mathbb{Z}},\;\elemOf{\sym{j}}{\oneTo{\sym{q}}} \]Then we can restate the earlier definition: a set of generators is a set of elements such that every other element of the group can be written as group word over the set.
Presentations #
A presentation of a group \( \group{G} \) is the data:
\[ \groupPresentation{\groupGenerator{g_1},\groupGenerator{g_2},\groupGenerator{\elSy},\groupGenerator{g_{\sym{n}}}}{\groupRelator{R_1},\groupRelator{R_2},\groupElement{\elSy},\groupRelator{R_{\sym{m}}}} \]where the \( \groupElement{g}_{\sym{i}} \) are generators of \( \group{G} \) and the \( \groupRelator{R_{\sym{j}}} \) are group words over the \( \groupElement{g}_{\sym{i}} \) called relators.
The relators are, by definition, equal to \( \groupElement{e} \), the identity element of the group. One can think of each relator as a concise way to encode an "identity" or "equation".
For example, consider the infinite Abelian group \( \group{\power{\group{\mathbb{Z}}}{2}} \), whose elements are the set \( \setConstructor{\TuFo{\sym{a}, \sym{b}}}{\elemOf{\sym{a},\sym{b}}{\mathbb{Z}}} \), identity \( \groupIdentity{e} = \TuFo{0, 0} \), with the group operation being elementwise addition.
Choosing generators \( \groupGenerator{x} = \TuFo{1, 0} \) and \( \groupGenerator{y} = \TuFo{0, 1} \), our presentation must now capture the fact that the group is Abelian, in other words, that the generators commute: \( \groupGenerator{x}\iGmult \groupGenerator{y} = \groupGenerator{y}\iGmult \groupGenerator{x} \). We can rewrite this identity as \( \groupCommutator{\groupGenerator{x}}{\groupGenerator{y}} = \groupGenerator{y}\iGmult \groupGenerator{x}\iGmult \groupInverse{\groupGenerator{y}}\iGmult \groupInverse{\groupGenerator{x}} = \groupIdentity{e} \), making the only relator of this group \( \groupCommutator{\groupGenerator{x}}{\groupGenerator{y}} \).
Therefore we have the following presentation for \( \group{\power{\group{\mathbb{Z}}}{2}} \) (which we will name \( \translationPresentation{2} \)):
\[ \translationPresentation{2}\defEqualSymbol \groupPresentation{\groupGenerator{x},\groupGenerator{y}}{\groupCommutator{\groupGenerator{x}}{\groupGenerator{y}}} \]There are many presentations of a given group, since we can rewrite relations in terms of each other, and similarly with generators.
Note: when naming presentations, there is ambiguity about whether the term \( \translationPresentation{2} \) refers to the presentation itself or the group it generates. We'll resolve this ambiguity using English, saying "the group presented by \( \translationPresentation{2} \)".
Free groups #
The free group on \( \sym{n} \) generators, written \( \freeGroup{\sym{n}} \), is a group with presentation \( \groupPresentation{\groupGenerator{g_1},\groupGenerator{g_2},\groupGenerator{\elSy},\groupGenerator{g_{\sym{n}}}}{\emSeSy} \), in other words, the group with no relations. The elements of such a group are uniquely described by a group word: two group element are identical if and only if their words are also identical. Normally, relations prevent us from easily telling when two group words describe the same group element, since applying the relations to rewrite one group word may or may not produce the other word, and it can be arbitrarily hard to determine when this is the case (this is known as the word problem for the group). Free groups on more than 0 generators have infinitely many elements, since we can form group words of arbitrary length by combining any number of \( \groupGenerator{g_{\sym{i}}} \) as we please.
The free Abelian group on \( \sym{n} \) generators is a group with presentation \( \groupPresentation{\groupGenerator{g_1},\groupGenerator{g_2},\groupGenerator{\elSy},\groupGenerator{g_{\sym{n}}}}{\groupCommutator{\groupGenerator{g_{\sym{i}}}}{\groupGenerator{g_{\sym{j}}}}} \). It is like the free group, but we also have that the generators all commute, and hence a group element is uniquely determine by the counts of the possible \( \groupGenerator{g_{\sym{i}}} \) in the word (with these counts being negative to indicate the inverses of \( \groupGenerator{g_{\sym{i}}} \)'s).
Cayley quivers #
We now give a simple way to generate a cardinal quiver from a group, which we'll call a Cayley quiver. This construction was originally developed by Arthur Cayley, who showed how to produce the so-called Cayley graph -- but we call these Cayley quivers to emphasize that they do in fact have a natural cardinal structure on them.
Let \( \group{G} \) be a group, with generators \( \setSymbol{J} = \list{\groupGenerator{\reFo{j_1}},\groupGenerator{\blFo{j_2}},\elSy} \). Then \( \bindCayleyQuiver{\group{G}}{\reFo{\card{c_1}}\bindingRuleSymbol \groupGenerator{\reFo{j_1}},\blFo{\card{c_2}}\bindingRuleSymbol \groupGenerator{\blFo{j_2}},\elSy} \) is the Cayley quiver on these generators, where cardinal \( \card{c_{\sym{i}}} \) represents generator \( \groupGenerator{j_{\sym{i}}} \). We can also write just \( \bindCayleyQuiver{\group{G}}{\groupGenerator{\reFo{j_1}},\groupGenerator{\blFo{j_2}},\elSy} \) or \( \bindCayleyQuiver{\group{G}}{\setSymbol{J}} \) if we use the same symbols \( \card{j},\groupGenerator{j} \) for the generators and cardinals.
The vertices and edges of the Cayley quiver \( \bindCayleyQuiver{\group{G}}{\sym{J}} \) are defined as follows:
\[ \begin{aligned} \vertexList(\bindCayleyQuiver{\group{G}}{\setSymbol{J}})&\defEqualSymbol \group{G}\\ \edgeList(\bindCayleyQuiver{\group{G}}{\setSymbol{J}})&\defEqualSymbol \setConstructor{\tde{\groupElement{g}}{\groupElement{g}\Gmult \groupGenerator{j}}{\card{j}}}{\elemOf{\groupElement{g}}{\group{G}},\;\elemOf{\groupGenerator{j}}{\setSymbol{J}}}\end{aligned} \]In other words, the vertices of \( \bindCayleyQuiver{\group{G}}{\setSymbol{J}} \) are elements of the group, and the edges are the transitions between elements that occur when right-multiplying by a generator \( \groupGenerator{j} \). Each edge is labeled by the cardinal \( \card{j} \) for that generator.
Cayley quivers from presentations #
A Cayley quiver \( \bindCayleyQuiver{\group{G}}{\sym{J}} \) is defined by a group \( \group{G} \) and a choice of generators \( \sym{J} = \list{\groupGenerator{\reFo{j_1}},\groupGenerator{\blFo{j_2}},\elSy} \) of \( \group{G} \). But a group presentation \( \presentation{Z} = \groupPresentation{\groupGenerator{\reFo{j_1}},\groupGenerator{\blFo{j_2}},\groupGenerator{\elSy}}{\groupElement{\elSy}} \) of \( \group{G} \) already specifies this choice of generators. Therefore we can talk about the Cayley quiver associated with such a group presentation \( \presentation{Z} \). We'll use a similar notation, writing just \( \cayleyQuiverSymbol{\presentation{Z}} \), or \( \bindCayleyQuiver{\presentation{Z}}{\groupGenerator{\card{c}_1},\groupGenerator{\card{c}_2},\elSy} \) if we wish to specify to explicitly name the cardinals corresponding to the generators of the presentation.
Example: Cyclic group #
Let's explore a very simple example: the cyclic group \( \cyclicGroup{\sym{n}} \) for \( \sym{n} = 3 \). We can write the elements of this group in terms of a generator \( \groupGenerator{g} \), and since 3 is prime, we can use any non-identity element to do this:
\[ \cyclicGroup{3} = \list{\groupIdentity{e},\groupGenerator{g},\groupPower{\groupGenerator{g}}{2}} \]We obtain the Cayley quiver \( \bindCayleyQuiver{\cyclicGroup{3}}{\groupGenerator{g}} \), shown below:
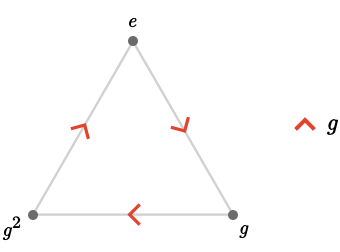
This is isomorphic to the 3-cycle quiver \( \subSize{\cycleQuiver }{3} \).
We now construct and name the obvious presentation of the cyclic group \( \cyclicGroup{\sym{n}} \) for arbitrary \( \sym{n} \). The name we'll use will look a little strange at first, but will make more sense from the perspective of Toroidal lattices:
\[ \bindCardSize{\translationPresentation{1}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{n}}}\defEqualSymbol \groupPresentation{\reFo{\groupGenerator{r}}}{\groupPower{\reFo{\groupElement{r}}}{\sym{n}}} \]We can now state the general fact that Cayley quivers of these presentations are isomorphic to cyclic quivers:
\[ \bindCardSize{\cayleyQuiverSymbol{\translationPresentation{1}}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{n}}}\isomorphicSymbol \bindCardSize{\subSize{\cycleQuiver }{\sym{n}}}{\reFo{\card{r}}} \]Example: integers #
Consider \( \group{\mathbb{Z}} \), the group of the integers under addition. Then it's not hard to see that \( \bindCayleyQuiver{\group{\mathbb{Z}}}{\groupGenerator{1}} \), the Cayley quiver using the integer 1 as the generator, is the following infinite quiver:

Let us name the obvious presentation \( \translationPresentation{1} \) of \( \group{\mathbb{Z}} \):
\[ \bindCardSize{\translationPresentation{1}}{\groupGenerator{\reFo{r}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}}}{\emSeSy} \]The Cayley quiver of this presentation is isomorphic to the line quiver:
\[ \cayleyQuiverSymbol{\translationPresentation{1}}\isomorphicSymbol \subSize{\lineQuiver }{ \infty } \]Example: integer plane #
Consider \( \group{\power{\group{\mathbb{Z}}}{2}} \), the group of pairs of integers under addition. Then \( \bindCayleyQuiver{\group{\power{\group{\mathbb{Z}}}{2}}}{\TuFo{1, 0},\TuFo{0, 1}} \) is the square quiver, a fragment shown below:

Let's construct a presentation of \( \groupPower{\group{\mathbb{Z}}}{2} \) and name it \( \translationPresentation{2} \). It’s easy to check that this is a presentation of the group \( \groupPower{\group{\mathbb{Z}}}{2} \) via \( \groupGenerator{\reFo{r}}\isomorphicSymbol \TuFo{1, 0},\groupGenerator{\blFo{b}}\isomorphicSymbol \TuFo{0, 1} \).
\[ \bindCardSize{\translationPresentation{2}}{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\blFo{b}}}} \]Then Cayley quiver of this presentation is isomorphic to the square quiver:
\[ \cayleyQuiverSymbol{\translationPresentation{2}}\isomorphicSymbol \subSize{\squareQuiver }{ \infty } \]Example: triangular plane #
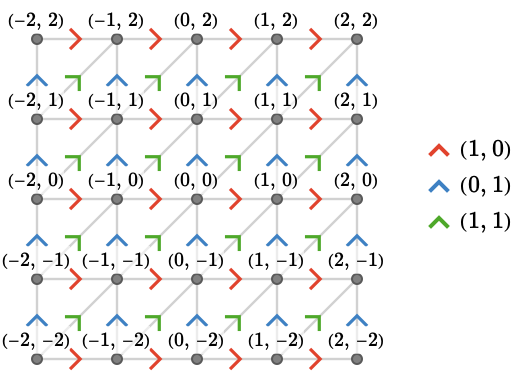
Staying with \( \group{\power{\group{\mathbb{Z}}}{2}} \), we now examine the Cayley quiver \( \bindCayleyQuiver{\group{\power{\group{\mathbb{Z}}}{2}}}{\TuFo{1, -1, 0},\TuFo{0, 1, -1},\TuFo{-1, 0, 1}} \), a fragment shown below:
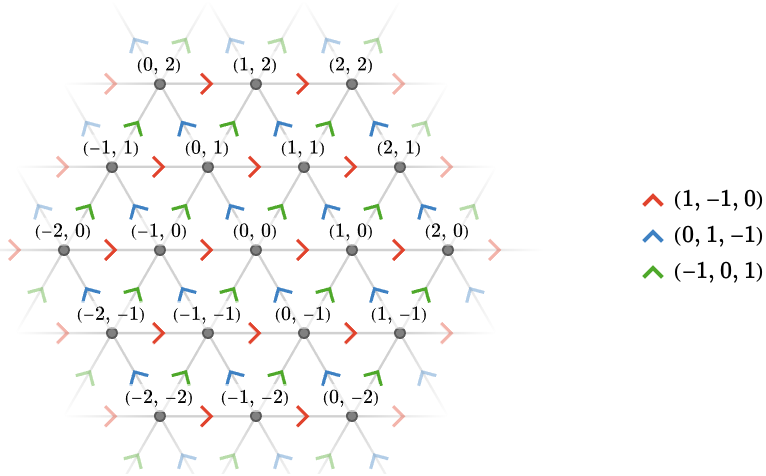
We name a presentation \( \starTranslationPresentation{3} \) of \( \group{\power{\group{\mathbb{Z}}}{2}} \) below.
\[ \bindCardSize{\starTranslationPresentation{3}}{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\grFo{g}}},\groupCommutator{\groupGenerator{\grFo{g}}}{\groupGenerator{\blFo{b}}},\groupGenerator{\reFo{r}}\iGmult \groupGenerator{\grFo{g}}\iGmult \groupInverse{\groupGenerator{\blFo{b}}}} \]Again, it’s easy to verify that this is a presentation of \( \group{\power{\group{\mathbb{Z}}}{2}} \) via generators \( \groupGenerator{\reFo{r}}\isomorphicSymbol \TuFo{1, -1, 0},\groupGenerator{\grFo{g}}\isomorphicSymbol \TuFo{0, 1, -1},\groupGenerator{\blFo{b}}\isomorphicSymbol \TuFo{-1, 0, 1} \), which satisfy the relators, since e.g. \( \TuFo{1, -1, 0} + \TuFo{0, 1, -1} = \minus{\TuFo{-1, 0, 1}} \).
The Cayley quiver of this presentation is isomorphic to the triangular quiver:
\[ \cayleyQuiverSymbol{\starTranslationPresentation{3}}\isomorphicSymbol \subSize{\triangularQuiver }{ \infty } \]Dependence on generators #
Notice the important fact that the two presentations of \( \group{\power{\group{\mathbb{Z}}}{2}} \) given by \( \starTranslationPresentation{3} \) and \( \translationPresentation{2} \) result in non-isomorphic Cayley quivers, being the triangular quiver and the square quiver respectively. This demonstrates that the choice of generators does matter.
Example: free group #
Consider \( \freeGroup{\sym{J}} \), the free group on two generators \( \sym{J} = \list{\groupGenerator{\reFo{j_1}},\groupGenerator{\blFo{j_2}}} \). The (infinite) Cayley quiver \( \bindCayleyQuiver{\freeGroup{\sym{J}}}{\sym{J}} \) is:
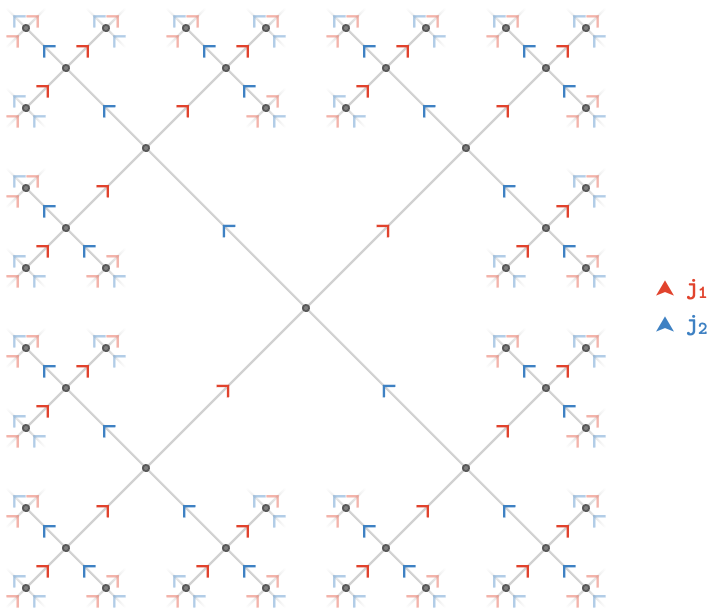
Generalizing to \( \sym{J} \) of arbitrary size, we have that:
\[ \bindCayleyQuiver{\freeGroup{\sym{J}}}{\sym{J}}\isomorphicSymbol \subSize{\treeQuiver{\setCardinality{\sym{J}}}}{ \infty } \]Example: Sym(3) #
Consider the symmetric group \( \graph{G} = \symmetricGroup{3} \). It can be generated by the transpositions \( \sym{J} = \list{\transposition{1}{2},\transposition{2}{3}} \). The Cayley quiver \( \bindCayleyQuiver{\graph{G}}{\sym{J}} \) is:
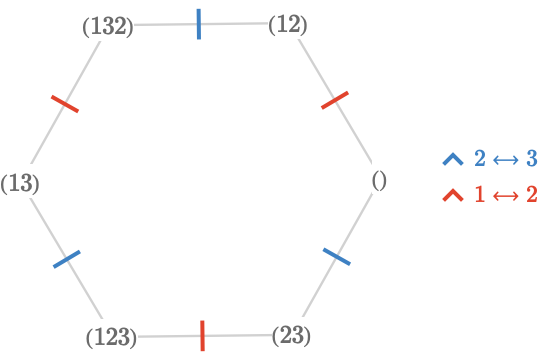
Each vertex is labeled with the cycle form of the corresponding permutation in \( \symmetricGroup{3} \).
Choice of generators #
As we saw above with the two presentations of \( \group{\power{\group{\mathbb{Z}}}{2}} \) given by \( \starTranslationPresentation{3} \) and \( \translationPresentation{2} \), different choices of generators for the same group can produce non-isomorphic Cayley quivers. As a further example example, let us revisit the presentation of the integer plane:
\[ \bindCardSize{\translationPresentation{2}}{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\blFo{b}}}} \]We can obtain a different presentation by introducing an additional generator \( \groupGenerator{\grFo{g}} \) with associated relator \( \groupGenerator{\grFo{g}} = \groupGenerator{\reFo{r}}\iGmult \groupGenerator{\blFo{b}} \). In \( \group{\power{\group{\mathbb{Z}}}{2}} \) \( \groupGenerator{\grFo{g}} \) is realized as \( \groupGenerator{\grFo{g}}\isomorphicSymbol \TuFo{1, 1} \). The new presentation is:
\[ \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\blFo{b}}},\groupGenerator{\reFo{r}}\iGmult \groupGenerator{\blFo{b}}\iGmult \groupInverse{\groupGenerator{\grFo{g}}}} \]This presents the same group \( \group{\power{\group{\mathbb{Z}}}{2}} \) because we can write any word in this new presentation in terms of the original generators \( \groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}} \) by replacing any \( \groupGenerator{\grFo{g}} \)’s with \( \groupGenerator{\reFo{r}}\iGmult \groupGenerator{\blFo{b}} \). So this is a redundant presentation.
Its associated Cayley quiver looks like this:
Another example is provided by choosing different generators of the symmetric group \( \symmetricGroup{3} \). Instead of \( \sym{J} = \list{\reFo{\transposition{1}{2}},\blFo{\transposition{2}{3}}} \), we shall choose \( \sym{J} = \list{\reFo{\transposition{1}{2}},\blFo{\permutationCycle{1\permutationCycleSymbol 2\permutationCycleSymbol 3\permutationCycleSymbol 1}}} \). This yields the following Cayley quiver \( \bindCayleyQuiver{\graph{G}}{\sym{J}} \):
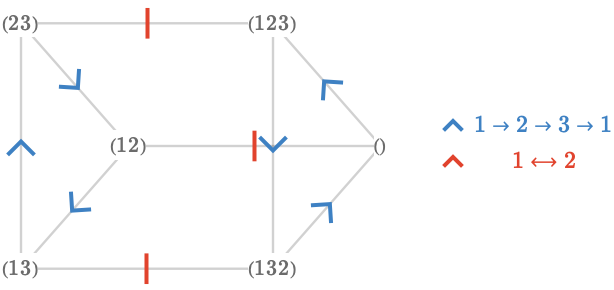
This triangular prism is clearly distinct from the hexagon we obtained from the original choice of generators. This fact can be deduced directly from the generators themselves: a cardinal corresponding to a transposition (a 2-cycle) must have order 2, and hence will have orbits in the Cayley quiver of that length. Likewise for cardinals corresponding to longer cycles.
Transitive quivers as Cayley quivers #
The above examples hopefully give the impression that the quivers we introduced in Transitive quivers appear to arise naturally as the Cayley quivers of simple groups. Notice that we cannot do this for finite quiver in each family (e.g. \( \subSize{\lineQuiver }{\sym{n}} \) for finite \( \sym{n} \)), since these are not actually transitive. Only for the infinite quivers such as \( \subSize{\lineQuiver }{ \infty } \) do we have Cayley quivers -- the exception being \( \subSize{\cycleQuiver }{\sym{n}} \) which is transitive for any \( \sym{n} \).
We can list these relationships in the form of a table, showing the quiver and corresponding group and group presentation that generates it as a Cayley quiver. We attach names to some of these presentations, as they will be generally useful:
| quiver | group | group presentation |
|---|---|---|
| \( \bindCards{\subSize{\lineQuiver }{ \infty }}{\reFo{\card{r}}} \) | \( \group{\mathbb{Z}} \) | \( \bindCardSize{\translationPresentation{1}}{\groupGenerator{\reFo{r}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}}}{\emSeSy} \) |
| \( \bindCards{\subSize{\cycleQuiver }{\sym{n}}}{\reFo{\card{r}}} \) | \( \cyclicGroup{\sym{n}} \) | \( \bindCardSize{\translationPresentation{1}}{\groupGenerator{\reFo{r}}\compactBindingRuleSymbol \modulo{\sym{n}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}}}{\groupPower{\groupGenerator{\reFo{r}}}{\sym{n}}} \) |
| \( \bindCards{\subSize{\squareQuiver }{ \infty }}{\reFo{\card{r}},\blFo{\card{b}}} \) | \( \groupPower{\group{\mathbb{Z}}}{2} \) | \( \bindCardSize{\translationPresentation{2}}{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\blFo{b}}}} \) |
| \( \bindCards{\subSize{\triangularQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \) | \( \groupPower{\group{\mathbb{Z}}}{2} \) | \( \bindCardSize{\starTranslationPresentation{3}}{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\grFo{g}}},\groupCommutator{\groupGenerator{\grFo{g}}}{\groupGenerator{\blFo{b}}},\groupGenerator{\reFo{r}}\iGmult \groupGenerator{\grFo{g}}\iGmult \groupInverse{\groupGenerator{\blFo{b}}}} \) |
| \( \bindCards{\subSize{\cubicQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \) | \( \groupPower{\group{\mathbb{Z}}}{3} \) | \( \bindCardSize{\translationPresentation{3}}{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\grFo{g}}},\groupCommutator{\groupGenerator{\grFo{g}}}{\groupGenerator{\blFo{b}}}} \) |
| \( \subSize{\gridQuiver{\sym{k}}}{ \infty } \) | \( \groupPower{\group{\mathbb{Z}}}{\sym{k}} \) | \( \bindCardSize{\translationPresentation{\sym{k}}}{\card{\card{c}_1},\elSy,\card{\card{c}_{\sym{k}}}}\defEqualSymbol \groupPresentation{\groupGenerator{\card{c}_{\sym{i}}}}{\groupCommutator{\groupElement{\card{c}_{\sym{i}}}}{\groupElement{\card{c}_{\sym{j}}}}} \) |
| \( \subSize{\treeQuiver{\sym{k}}}{ \infty } \) | \( \freeGroup{\sym{C}} \) | \( \groupPresentation{\groupGenerator{\card{c}_{\sym{i}}}}{\emSeSy} \) |
| \( \bouquetQuiver{\sym{k}} \) | \( \list{\groupElement{e}} \) | \( \groupPresentation{\groupGenerator{\card{c}_{\sym{i}}}}{\groupElement{\card{c}_{\sym{i}}}} \) |
Some notes: for the final three rows, we write \( \card{c}_{\sym{i}} \) to denote the sequence \( \card{c}_1,\elSy,\card{c}_{\sym{k}} \), etc. Lastly, the presentation \( \groupPresentation{\groupGenerator{\card{c}_{\sym{i}}}}{\groupElement{\card{c}_{\sym{i}}}} \) is "degenerate": the \( \card{c}_{\sym{i}} \) here are actually all the identity element \( \groupElement{e} \) of the trivial group \( \list{\groupElement{e}} \).