Graphs and quivers #
Graphs #
We started with the intuition that geometry should be about states/places: \( \vert{x},\vert{y},\vert{z} \) and their transitions: \( \tde{\vert{x}}{\vert{y}}{\card{a}} \), \( \tde{\vert{y}}{\vert{z}}{\card{b}} \), etc. Evidently we have the main ingredients of a graph, specifically a directed graph:
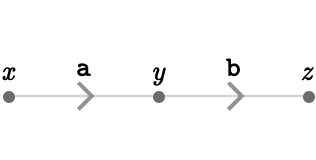
The objects \( \vert{x},\vert{y},\vert{z} \) are called vertices. \( \tde{\vert{x}}{\vert{y}}{\card{a}} \) is a labeled edge, where \( \card{a} \) is the label, which we call a cardinal. The unlabelled form is written \( \de{\vert{x}}{\vert{y}} \). \( \vert{x} \) is called the tail vertex and \( \vert{y} \) is called the head vertex of the edge. When vertices represent states and edges represent transitions between states, we’ll use the terms vertex/state and edge/transition synonymously.
It turns out that we will have to consider specific kinds of directed graphs if we wish to build a notion of geometry. These graphs are quivers, also known as directed multigraphs, which are directed graphs that allow multiple edges as well as cycles between any pair of vertices:
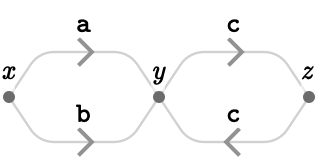
Cardinal quivers #
A seemingly fundamental geometrical idea is that of a direction.
For discrete geometry, a direction will take the form of a label for an entire set of transitions: these are the transitions that, although they are between different pairs of vertices, are all in the same direction (in whatever sense). We’ll call this label a cardinal, by analogy with the cardinals of a compass \( \list{\card{N},\card{E},\card{S},\card{W}} \). We'll write cardinals in a typewriter font to distinguish them from symbols representing vertices, etc.
A cardinal quiver is a quiver whose edges are labeled with symbols called cardinals, with some additional properties. First, while we will allow the number of vertices and edges of the quiver to be countably infinite, we will restrict the number of cardinals to be finite. Additionally, the labeling of edges by cardinals must satisfy the property of local uniqueness:
- the list of cardinals on edges {entering, leaving} a given vertex cannot contain duplicates
For example, the situation \( \tde{\vert{y}}{\vert{x}}{\card{c}},\tde{\vert{y}}{\vert{z}}{\card{c}} \) is forbidden, as the cardinal \( \card{c} \) occurs twice when leaving \( \vert{y} \). In contrast, the situation \( \tde{\vert{x}}{\vert{y}}{\card{c}},\tde{\vert{y}}{\vert{z}}{\card{c}} \) is permitted, as \( \card{c} \) occurs entering \( \vert{y} \) once and leaving \( \vert{y} \) once. Some more examples of forbidden and permitted situations are shown below:
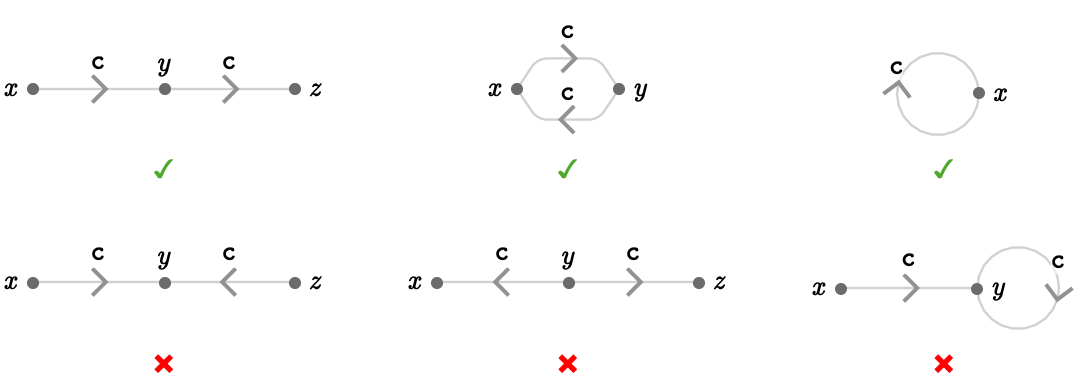
This uniqueness property has a very important purpose: it ensures that a pair of a vertex and a cardinal \( \TuFo{\vert{v}, \card{c}} \) will unambiguously identify an edge (if one exists), since there can only be one edge starting at \( \vert{v} \) that is labeled by \( \card{c} \). This corresponds to the basic requirements of the notion of a direction: it unambiguously identifies the navigational choices an agent should make. As a motivation: for "north" to be a direction, there cannot be two ways to go north from one location that lead to different locations.
Cardinal quivers will be our focus, so I’ll refer to them as quivers to avoid cumbersome language. If we need to refer to the classical notion of a quiver as a directed multigraph, we’ll use the term unlabelled quiver.
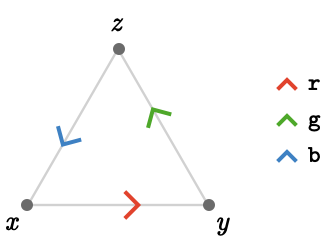
Since cardinals will almost always label multiple edges in a quiver, we will use color to represent the edges labeled by each cardinal, and choose cardinal letters e.g. \( \reFo{\card{r}} \), \( \grFo{\card{g}} \), \( \blFo{\card{b}} \) to reflect these colors:
Here are more examples -- since the arrowhead color indicates the name of the cardinal, we'll drop the legends. The cardinals label multiple edges, but still obey local uniqueness:
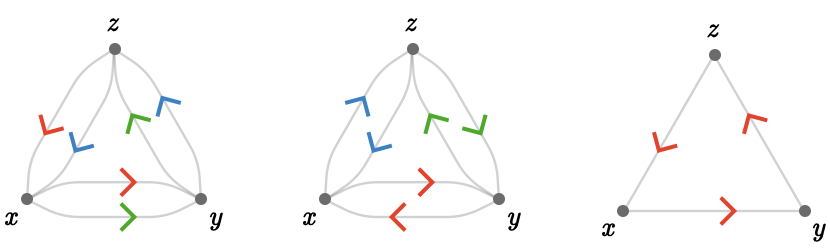
Note that the right-most example has some of the intuitive aspects of an actual discrete geometry: the cardinal \( \reFo{\card{r}} \) can be taken (meaning a move in the direction \( \reFo{\card{r}} \) can be made) for any of the states \( \vert{x},\vert{y},\vert{z} \). Taking \( \reFo{\card{r}} \) repeatedly simply cycles through these states: a discrete analog of a circle.
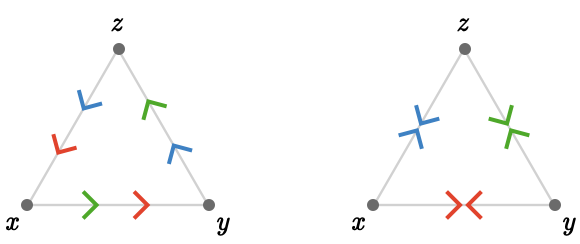
For simplicity, we can depict quivers that contains multiple edges between the same vertices by combining the edges, using multiple arrowheads instead. Using this convention the first two quivers above look as follows:
Enumeration #
Since finite, connected quivers will play a major role in this series, it is interesting to enumerate all the finite connected quivers of a given size.
One way to organize this enumeration is in terms of what we’ll call quiver skeletons, which are undirected simple graphs (graphs without multiple edges between vertices) that serve as templates for quivers. We can enumerate these skeletons by fixing the number of vertices, then taking all possible sets of undirected edges between these vertices that include each vertex at least once and still produce a connected graph. We count these quiver skeletons up to graph isomorphism, in other words, the labeling of the vertices of these graphs is not significant.
Here is a gallery that shows the quiver skeletons for each vertex count:
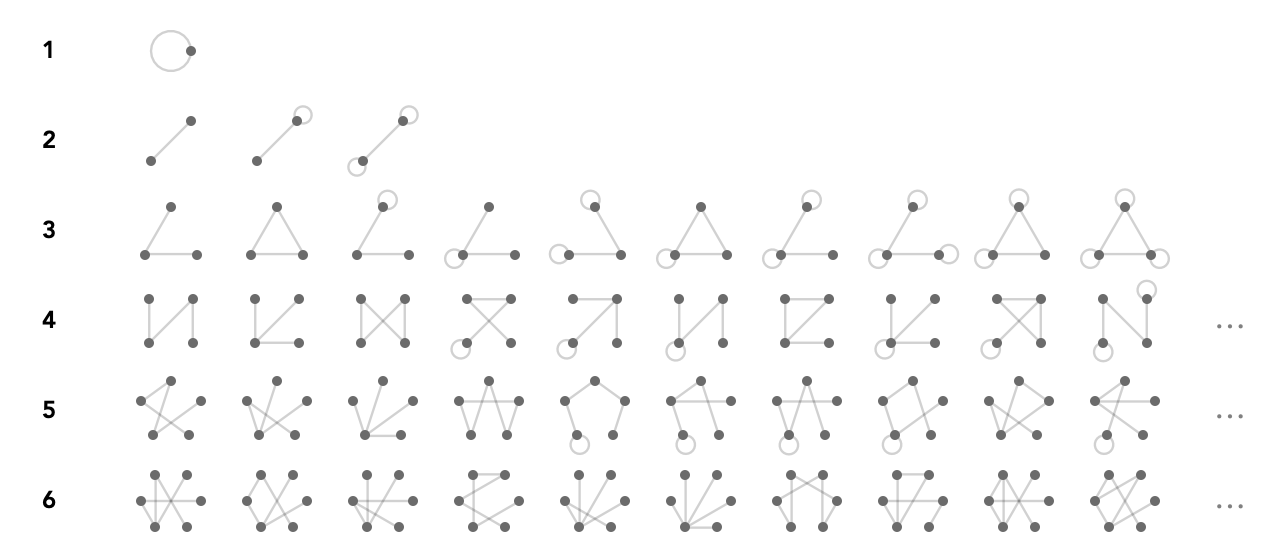
The number of skeletons for \( \sym{n} \) vertices is the sequence \( \{1,3,10,50,354,3883,...\} \), which is not yet in the Online Encyclopedia of Integer Sequences (OEIS).
Once we have chosen a particular skeleton, we can then go about attaching cardinal structure to it to turn it into a quiver (which recall means a cardinal quiver). Typically there are multiple possible choices, although there is an obvious symmetry we must take into account: we can perform any global renaming of cardinals and we’ll still have the same essential cardinal quiver. More generally, the action of the relevant symmetry group is the simultaneous relabeling of vertices, edges, and cardinals:
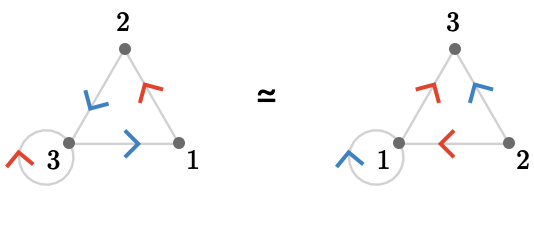
Here, the vertices have been rewritten \( \list{\rewrite{1}{2},\rewrite{2}{3},\rewrite{3}{1}} \) and the cardinals have been rewritten \( \list{\rewrite{\reFo{\card{r}}}{\blFo{\card{b}}},\rewrite{\blFo{\card{b}}}{\reFo{\inverted{\card{r}}}}} \) -- note the underbar on \( \reFo{\inverted{\card{r}}} \), which indicates we flip the cardinal direction when rewriting \( \blFo{\card{b}} \) to \( \reFo{\card{r}} \). We call two such quivers to be strongly isomorphic, or just isomorphic. We distinguish this from weakly isomorphic quivers, which are isomorphic as directed graphs but whose cardinal structure is not necessarily preserved -- in other words, there is no rewriting of cardinals that can relate the cardinal structure of the first and second quivers.
Let’s look at some examples of the quivers associated with skeletons. We’ll only visualize the cases involving 3 or fewer cardinals, since the number of quivers rapidly increases as a function of the number of cardinals.
Taking the skeleton on the first row, which is a one-vertex graph with a self-loop, there is exactly one possible quiver for a given number of cardinals:
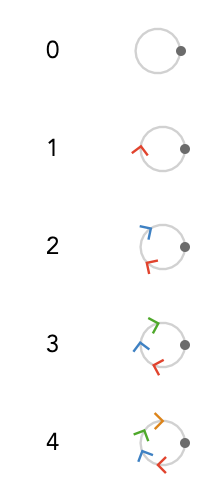
These quivers are called bouquet quivers.
Taking the $2^{\textrm{nd}}$ skeleton on the $2^{\textrm{nd}}$ row as another example, there are 0 quivers with 1 cardinal, 3 quivers with 2 cardinals, and 9 quivers with 3 cardinals. (The ‘flat’ arrowheads below indicate that a cardinal is present in both orientations on that edge).

The numbers of quivers for this skeleton as a function of the number of cardinals is \( \{0,3,9,19,34,55,83,119,164,219,...\} \). The empirically-found closed form for this sequence appears to be \( 6^{-1}n^3+2^{-1}n^2+3^{-1}n-1 \).
For the $1^{\textrm{st}}$ skeleton on the $2^{\textrm{nd}}$ row, there are 2 quivers with 1 cardinal, 4 quivers with 2 cardinals, and 6 quivers with 3 cardinals:

The numbers of quivers for this skeleton as a function of the number of cardinals is \( \{2,4,6,9,12,16,20,25,30,36,42,49,...\} \), with empirically-found closed form \( 4^{-1}n^2+n+8^{-1}(7+(-1)^n) \).
For the $1^{\textrm{st}}$ skeleton on the $3^{\textrm{rd}}$ row, there is only 1 quiver with 1 cardinal, 16 quivers with 2 cardinals, and 64 quivers with 3 cardinals:
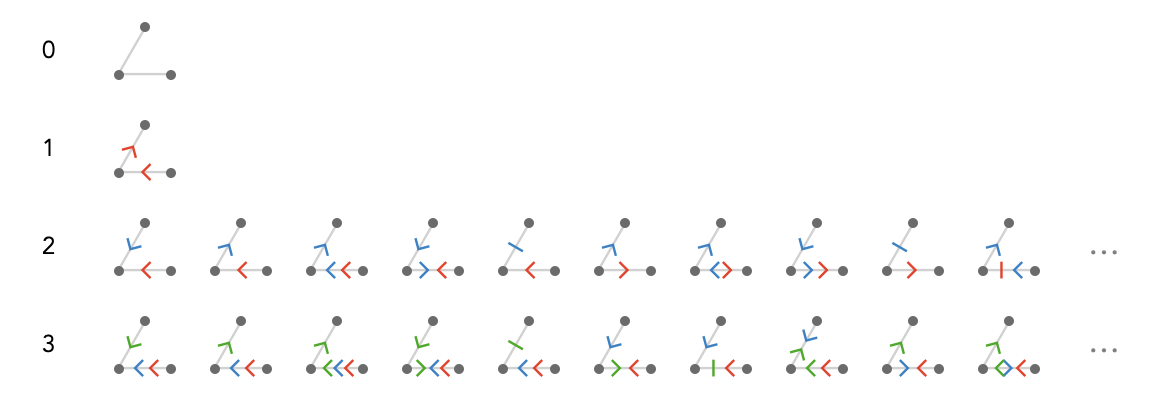
The numbers of quivers for this skeleton as a function of the number of cardinals is \( \{1,16,64,211,551,1276,2672,...\} \). No simple closed form is apparent, though one probably exists.
The following table summarizes the number of quivers that can be obtained from the skeletons with fewer than 4 vertices. The columns indicate skeletons, and the rows numbers of cardinals, and the entries indicate the number of quivers:
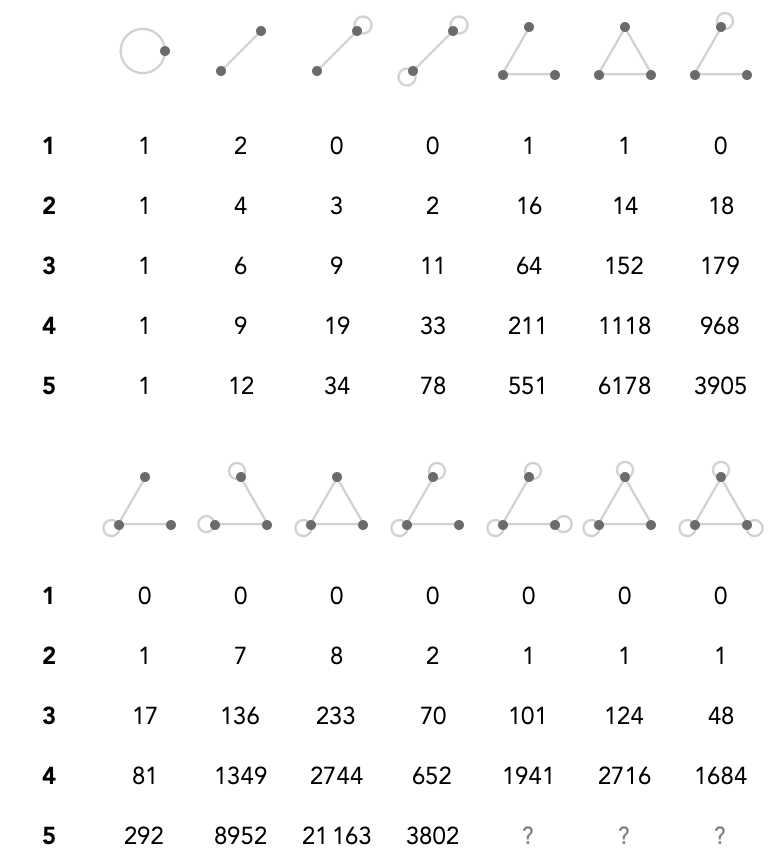
Only the first 3 columns of this table are in the OEIS.
The number of 5-cardinal quivers for the final 3 skeletons are too expensive to compute in a straightforward way, these are marked with a ? in the table.
Moving on to skeletons with 4 vertices, of which there are 50, we have this table:
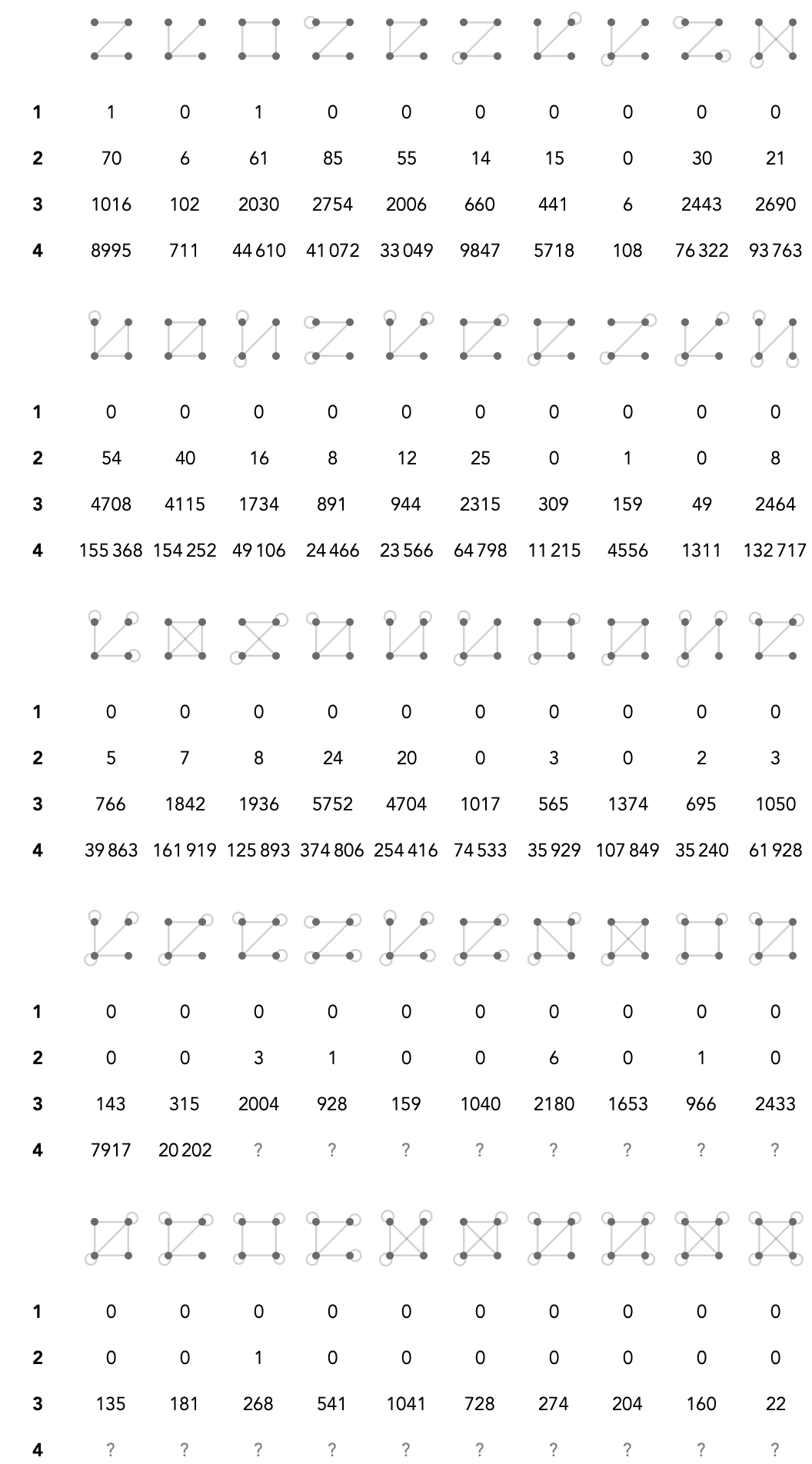
Finally, by summing over the tables above, we can obtain a bird’s eye view that captures how many quivers there are as a function of number of vertices \( n \) and cardinals \( c \):
Clearly, beyond \( \sym{n} = 1 \), even for modest values of \( \sym{c} \), we find our armory overflowing with quivers!