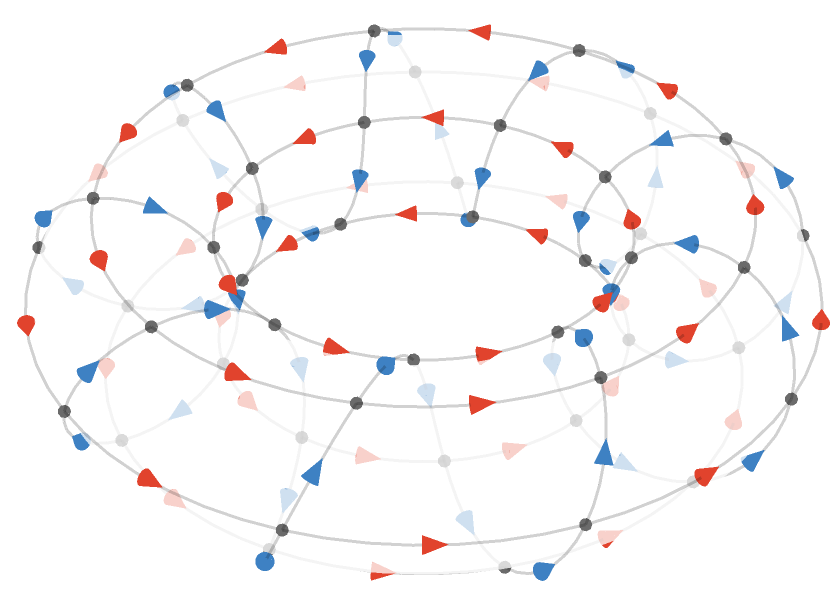
Toroidal lattices #
Introduction #
In Lattice quivers, we examined lattice quivers, which were the Cayley quivers determined by particular group presentations \( \translationPresentation{\sym{n}},\starTranslationPresentation{\sym{n}} \) of infinite Abelian groups \( \group{\power{\group{\mathbb{Z}}}{\sym{n}}} \). We could also see these quivers as the path quotients of a fundamental quiver \( \quiver{F} = \bouquetQuiver{\sym{n}} \) by affine path valuations \( \translationPathValuation{\sym{n}},\starTranslationPathValuation{\sym{n}} \) valued in Abelian groups \( \group{\power{\group{\mathbb{Z}}}{\sym{n}}} \). The benefit of taking this more abstract path quotient perspective was that more complex choices of fundamental quiver \( \quiver{F} \) can generate the hexagonal, rhombille, etc. lattices -- we developed this idea in Intransitive lattices.
The generalization we pursue in this section is to swap out the infinite groups \( \group{\power{\group{\mathbb{Z}}}{\sym{n}}} \) for finite Abelian groups. These yield finite lattice quivers that we can visualize as lattices defined on a torus. Furthermore, by choosing direct products of groups, some of which are finite (\( \cyclicGroup{\sym{n}} \)), and others which are infinite (\( \group{\mathbb{Z}} \)), we can obtain "partial tori", or cylinders.
Square torus #
Square quiver #
Recall that the square quiver \( \bindCardSize{\subSize{\squareQuiver }{ \infty }}{\reFo{\card{r}},\blFo{\card{b}}} \) can be seen in two ways:
-
as the Cayley quiver \( \bindCardSize{\cayleyQuiverSymbol{\translationPresentation{2}}}{\reFo{\card{r}},\blFo{\card{b}}} \), where \( \bindCardSize{\translationPresentation{2}}{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\blFo{b}}}} \) is a presentation of \( \group{\power{\group{\mathbb{Z}}}{2}} \).
-
as the path quotient \( \compactQuotient{\quiver{F}}{\vert{o}}{\translationWordHomomorphism{2}} \) of the fundamental quiver \( \quiver{F} = \bouquetQuiver{2} \) by the affine path valuation \( \translationPathValuation{2} \).
Intuitively, the quotient takes the forward path quiver \( \forwardPathQuiver{\quiver{F}}{\vert{o}} \) (which is isomorphic to \( \subSize{\treeQuiver{2}}{ \infty } \)), and glues vertices together that share a path value under \( \translationPathValuation{2} \).
That \( \translationPathValuation{2} \) is affine is just the statement that a path value \( \function{\translationPathValuation{2}}(\path{P}) \) depends only on the path word via the group homomorphism \( \functionSignature{\function{\translationWordHomomorphism{2}}}{\wordGroup{\quiver{2}}}{\group{\power{\group{\mathbb{Z}}}{2}}} \):
\[ \function{\translationPathValuation{2}}(\path{P})\defEqualSymbol \function{\translationWordHomomorphism{2}}(\wordOf(\path{P})) \]The homomorphism \( \translationWordHomomorphism{2} \) just sends cardinals (the generators of \( \wordGroupSymbol \)) to the obvious generators of \( \group{\power{\group{\mathbb{Z}}}{2}} \) -- the behavior of \( \translationWordHomomorphism{2} \) on longer words \( \elemOf{\wordSymbol{W}}{\wordGroupSymbol } \) is uniquely determined by these images:
\[ \bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}},\blFo{\card{b}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\TuFo{1, 0}},\mto{\blFo{\card{b}}}{\TuFo{0, 1}}} \]We can see that these constructions are really the same: the forward path quiver \( \forwardPathQuiver{\quiver{F}}{\vert{o}} \) first constructs paths with all possible words, and the subsequent quotient \( \quotient{\forwardPathQuiver{\quiver{F}}{\vert{o}}}{\translationPathValuation{2}} \) by the affine path valuation \( \translationPathValuation{2} \) then identifies those paths that should be the same under relator (\( \reFo{\card{r}}\iGmult \blFo{\card{b}} = \blFo{\card{b}}\iGmult \reFo{\card{r}} \)) in the presentation \( \translationPresentation{2} \).
Torus #
We can construct a square torus quiver by replacing \( \group{\power{\group{\mathbb{Z}}}{2}} \) with \( \groupDirectProduct{\cyclicGroup{\sym{w}}\groupDirectProductSymbol \cyclicGroup{\sym{h}}} \) in either of these constructions.
Let's start with the group presentation \( \bindCardSize{\translationPresentation{2}}{\reFo{\card{r}},\blFo{\card{b}}} \) of \( \group{\power{\group{\mathbb{Z}}}{2}} \), which is:
\[ \bindCardSize{\translationPresentation{2}}{\reFo{\card{r}},\blFo{\card{b}}}\defEqualSymbol \groupPresentation{\reFo{\groupGenerator{r}},\blFo{\groupGenerator{b}}}{\groupCommutator{\reFo{\groupElement{r}}}{\blFo{\groupElement{b}}}} \]We now define the following presentation of \( \groupDirectProduct{\cyclicGroup{\sym{w}}\groupDirectProductSymbol \cyclicGroup{\sym{h}}} \), which imposes finitude, essentially saying that if we take the \( \reFo{\card{r}} \) cardinal \( \sym{w} \) times we should return to our starting vertex, etc:
\[ \bindCardSize{\translationPresentation{2}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}}\defEqualSymbol \groupPresentation{\reFo{\groupGenerator{r}},\blFo{\groupGenerator{b}}}{\groupCommutator{\reFo{\groupElement{r}}}{\blFo{\groupElement{b}}},\groupPower{\reFo{\groupElement{r}}}{\sym{w}},\groupPower{\blFo{\groupElement{b}}}{\sym{h}}} \]We can then define the square torus as the Cayley quiver of this presentation.
Alternatively, and equivalently, we can construct the square torus as a quotient by defining the "cyclic" affine path valuation induced by the group homomorphism we denote by \( \bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}} \):
\[ \begin{nsarray}{c} \functionSignature{\function{\bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}}}}{\wordGroup{\quiver{2}}}{\groupDirectProduct{\cyclicGroup{\sym{w}}\groupDirectProductSymbol \cyclicGroup{\sym{h}}}}\\ \\ \bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}}\defEqualSymbol \assocArray{\mto{\reFo{\card{r}}}{\TuFo{1, 0}},\mto{\blFo{\card{b}}}{\TuFo{0, 1}}} \end{nsarray} \]The parameters \( \sym{w},\sym{h} \) are the moduli of the torus, where \( \sym{w} \) is the width modulus and \( \sym{h} \) is the height modulus. We generalize our notation for finite square quivers, which was \( \bindCardSize{\squareQuiver }{\sym{w},\sym{h}} \), to allow for these finite but cyclic dimensions:
\[ \bindCardSize{\toroidalModifier{\squareQuiver }}{\sym{w},\sym{h}}\congruentSymbol \bindCardSize{\squareQuiver }{\modulo{\sym{w}},\modulo{\sym{h}}}\defEqualSymbol \compactQuotient{\bouquetQuiver{2}}{\vert{0}}{\bindCardSize{\translationWordHomomorphism{2}}{\modulo{\sym{w}},\modulo{\sym{h}}}}\congruentSymbol \bindCardSize{\cayleyQuiverSymbol{\translationPresentation{2}}}{\modulo{\sym{w}},\modulo{\sym{h}}} \]We suppressed the cardinals \( \reFo{\card{r}},\blFo{\card{b}} \), but we can also explicitly bind them in the notation:
\[ \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}}\defEqualSymbol \compactQuotient{\bindCardSize{\bouquetQuiver{2}}{\reFo{\card{r}},\blFo{\card{b}}}}{\vert{0}}{\bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}}}\congruentSymbol \bindCardSize{\cayleyQuiverSymbol{\translationPresentation{2}}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}} \]Below we show \( \bindCards{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{10},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{4}} \), the square torus with width modulus 10 and height modulus 4:
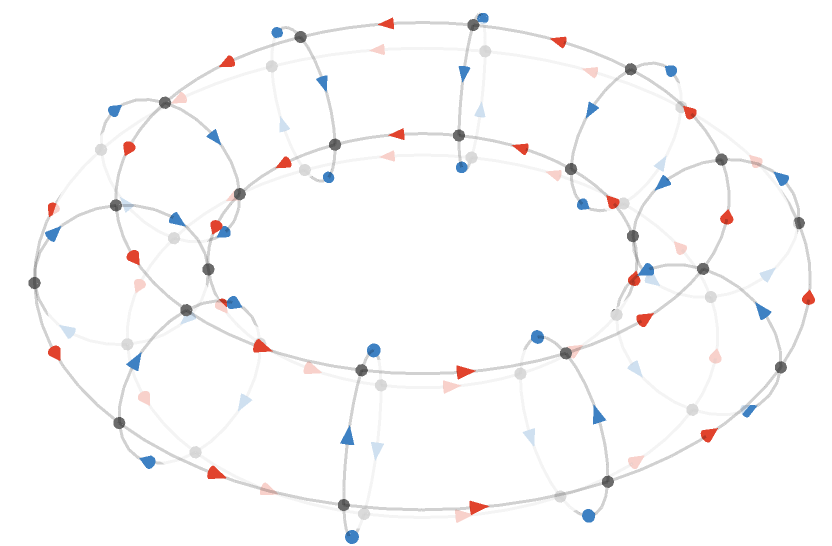
The \( \reFo{\card{x}} \) cardinal is associated with traversal around the outer radius of the torus, and the \( \blFo{\card{y}} \) cardinal with the inner radius. The outer radius spanned by \( \reFo{\card{x}} \) has a width modulus of 10, and the inner radius spanned by \( \blFo{\card{y}} \) has a height modulus of 4.
Path relations #
From a path-algebraic point of view, a square torus has a simple characterization. Recall that for the infinite square lattice, we have the single path relation \( \word{\reFo{\card{x}}}{\blFo{\card{y}}}\pathIso \word{\blFo{\card{y}}}{\reFo{\card{x}}} \). A square torus with moduli \( \TuFo{\sym{w}, \sym{h}} \) extends this to the set \( \list{\word{\reFo{\card{x}}}{\blFo{\card{y}}}\pathIso \word{\blFo{\card{y}}}{\reFo{\card{x}}},\repeatedPower{\word{\reFo{\card{x}}}}{\sym{w}}\pathIso \word{1},\repeatedPower{\word{\blFo{\card{y}}}}{\sym{h}}\pathIso \word{1}} \).
Square tori as generalizations of square quivers #
We now compare the square torus quiver \( \bindCards{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}} \) and the square quivers we defined in Transitive quivers: the ordinary finite square quiver \( \bindCards{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \sym{w},\blFo{\card{b}}\compactBindingRuleSymbol \sym{h}} \) and the infinite square quiver \( \bindCards{\subSize{\squareQuiver }{ \infty }}{\reFo{\card{r}},\blFo{\card{b}}}\congruentSymbol \bindCards{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \infty ,\blFo{\card{b}}\compactBindingRuleSymbol \infty } \).
Firstly, if we adopt the normal convention that the additive group of integers \( \group{\mathbb{Z}} \) is a cyclic group order infinity (\( \group{\mathbb{Z}} = \cyclicGroup{ \infty } \)), then we can see the infinite square quiver as being a square torus with infinite moduli. The last two path relations \( \list{\word{\reFo{\card{x}}}{\blFo{\card{y}}}\pathIso \word{\blFo{\card{y}}}{\reFo{\card{x}}},\repeatedPower{\word{\reFo{\card{x}}}}{\sym{w}}\pathIso \word{1},\repeatedPower{\word{\blFo{\card{y}}}}{\sym{h}}\pathIso \word{1}} \) become vacuous, leaving us with the ordinary path relations of the infinite square quiver \( \list{\word{\reFo{\card{x}}}{\blFo{\card{y}}}\pathIso \word{\blFo{\card{y}}}{\reFo{\card{x}}}} \).
Secondly, let's compare the finite square quiver \( \bindCards{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \sym{w},\blFo{\card{b}}\compactBindingRuleSymbol \sym{h}} \) with the square torus quiver \( \bindCards{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}} \) for e.g. \( \TuFo{\sym{w}, \sym{h}} = \TuFo{10, 4} \) . We will display the torus quiver on a 2-dimensional “modular plane” rather than in 3 dimensions. We can think of this plane as “wrapping around” on its border -- but we’ll number the edges that cross this border so that it is easy to trace how they connect up:

Compare this to the ordinary finite square quiver \( \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol 10,\blFo{\card{b}}\compactBindingRuleSymbol 4} \):
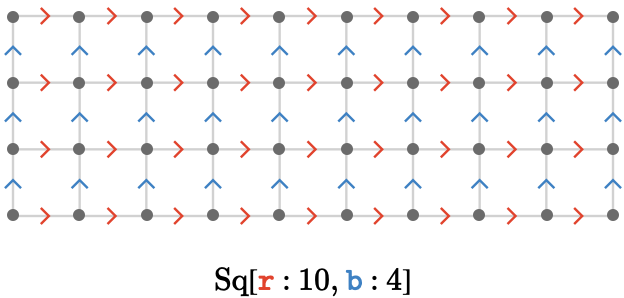
Clearly, the square torus has the same number of vertices, and differs only from the regular square quiver in that we have "glued the borders" together in the obvious way.
Square cylinder #
We've defined the square torus \( \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}} \), in which dimensions are cyclic. But what about the case in which only one is cyclic and the other is infinite, e.g. \( \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \infty ,\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{h}}} \)?
This is already well-defined if we consider the integers to be a cyclic group with infinite order (\( \group{\mathbb{Z}} = \cyclicGroup{ \infty } \)). We'll call these special tori cylinders.
Here we show a fragment of the square cylinder \( \bindCardSize{\squareQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \infty ,\blFo{\card{b}}\compactBindingRuleSymbol \modulo{5}} \) on the modular plane:
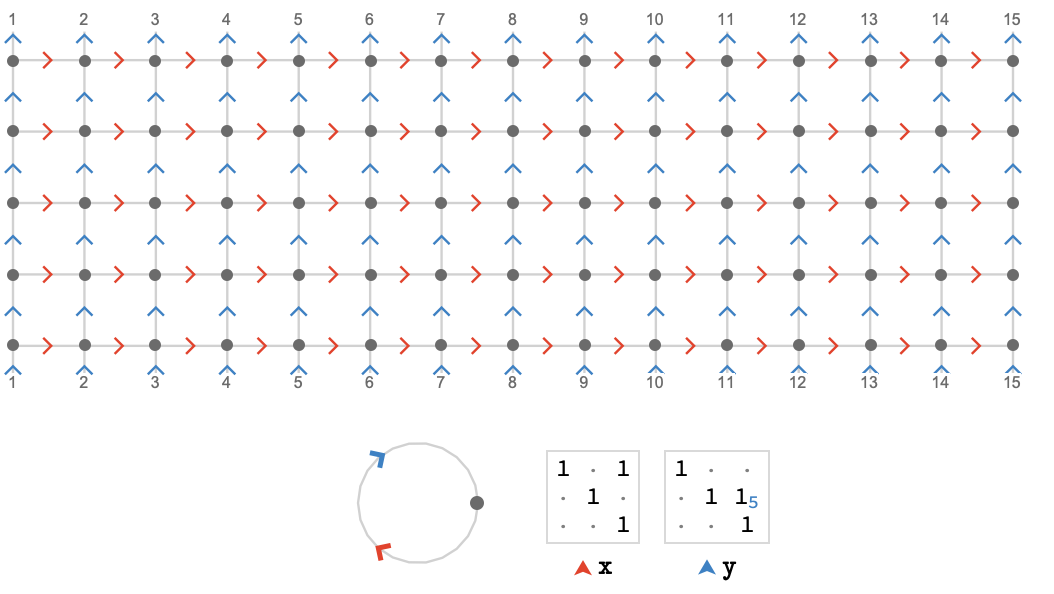
Here is the same cylinder in 3 dimensions:
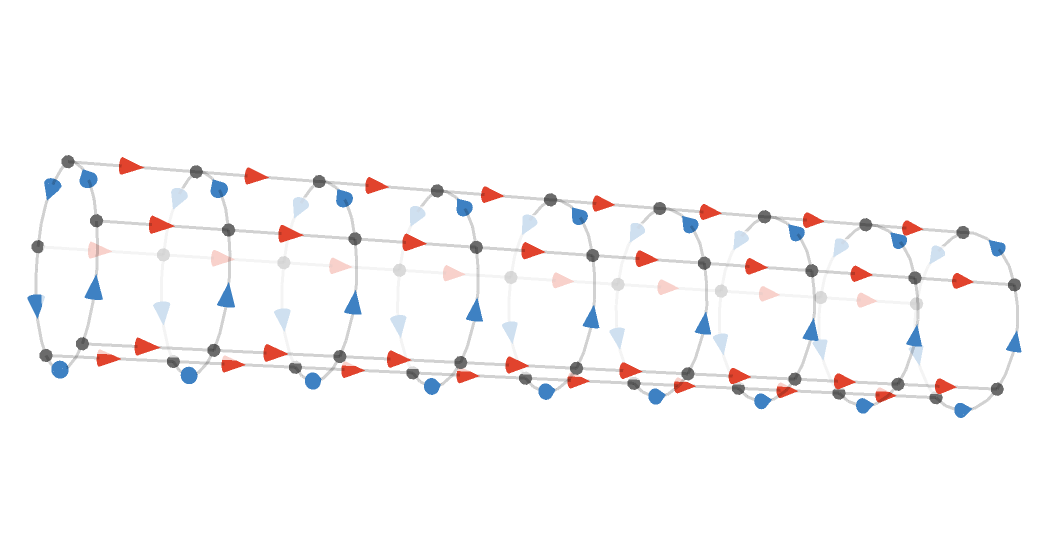
In general, we'll use the generic term tori to encompass both the cases where both cardinals have finite dimension, yielding a torus, and where one (or more) cardinal has infinite dimension, yielding a cylinder (or higher-dimensional analogue).
Triangular torus #
The construction we saw above gives toroidal and cyclindrical versions of the square, cubic, and indeed all the higher dimensional variants \( \gridQuiver{\sym{n}} \). But how can we obtain a toroidal triangular lattice?
As Cayley quiver #
The Cayley quiver construction is most natural. Recall the "triangular" group presentation \( \starTranslationPresentation{3} \) we introduced in Cayley quivers:
\[ \bindCardSize{\starTranslationPresentation{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\grFo{g}}},\groupCommutator{\groupGenerator{\grFo{g}}}{\groupGenerator{\blFo{b}}},\groupGenerator{\reFo{r}}\iGmult \groupGenerator{\grFo{g}}\iGmult \groupInverse{\groupGenerator{\blFo{b}}}} \]To make this group finite, we now define a related presentation that imposes additional relators that cause every element of this group to have finite order:
\[ \bindCardSize{\starTranslationPresentation{3}}{\groupGenerator{\reFo{r}}\compactBindingRuleSymbol \modulo{\sym{h}},\groupGenerator{\grFo{g}}\compactBindingRuleSymbol \modulo{\sym{w}},\groupGenerator{\blFo{b}}\compactBindingRuleSymbol \modulo{\sym{w}}}\defEqualSymbol \groupPresentation{\groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}}}{\groupCommutator{\groupGenerator{\reFo{r}}}{\groupGenerator{\grFo{g}}},\groupCommutator{\groupGenerator{\grFo{g}}}{\groupGenerator{\blFo{b}}},\groupGenerator{\reFo{r}}\iGmult \groupGenerator{\grFo{g}}\iGmult \groupInverse{\groupGenerator{\blFo{b}}},\groupPower{\groupGenerator{\reFo{r}}}{\sym{h}},\groupPower{\groupGenerator{\grFo{g}}}{\lcm(\sym{w},2 \, \sym{h})}} \]Two notes: the role of the lowest-common-multiple function will explained later. Also, the "missing relation" \( \groupPower{\groupGenerator{\blFo{b}}}{\lcm(\sym{w},2 \, \sym{h})} \) is implied by the other relations.
As path quotient #
We can use a similar method as before, except this time we adapt the homomorphism \( \starTranslationWordHomomorphism{3} \). We will cheat a little and define the toroidal form of \( \starTranslationWordHomomorphism{3} \) as a rather trivial map into the group presented by \( \bindCardSize{\starTranslationPresentation{3}}{\groupGenerator{\reFo{r}}\compactBindingRuleSymbol \modulo{\sym{h}},\groupGenerator{\grFo{g}}\compactBindingRuleSymbol \modulo{\sym{w}},\groupGenerator{\blFo{b}}\compactBindingRuleSymbol \modulo{\sym{w}}} \) that we just defined above -- we explained this connection in Lattice quivers.
\[ \begin{nsarray}{c} \functionSignature{\function{\bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{h}},\grFo{\card{g}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{w}}}}}{\wordGroup{\quiver{3}}}{\bindCardSize{\starTranslationPresentation{3}}{\groupGenerator{\reFo{r}}\compactBindingRuleSymbol \modulo{\sym{h}},\groupGenerator{\grFo{g}}\compactBindingRuleSymbol \modulo{\sym{w}},\groupGenerator{\blFo{b}}\compactBindingRuleSymbol \modulo{\sym{w}}}}\\ \\ \starTranslationWordHomomorphism{3}\defEqualSymbol \assocArray{\mto{\reFo{\card{r}}}{\groupGenerator{\reFo{r}}},\mto{\grFo{\card{g}}}{\groupGenerator{\grFo{g}}},\mto{\blFo{\card{b}}}{\groupGenerator{\blFo{b}}}} \end{nsarray} \]This map sends the cardinals \( \reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}} \) to the generators \( \groupGenerator{\reFo{r}},\groupGenerator{\grFo{g}},\groupGenerator{\blFo{b}} \) of the presentation. Then we define the torus to be the path quotient:
\[ \bindCardSize{\triangularQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{h}},\grFo{\card{g}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{w}}}\defEqualSymbol \compactQuotient{\bindCardSize{\bouquetQuiver{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}}{\vert{0}}{\bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{\sym{h}},\grFo{\card{g}}\compactBindingRuleSymbol \modulo{\sym{w}},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{\sym{w}}}} \]Here is the triangular torus \( \bindCardSize{\triangularQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{4},\grFo{\card{g}}\compactBindingRuleSymbol \modulo{8},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{8}} \):
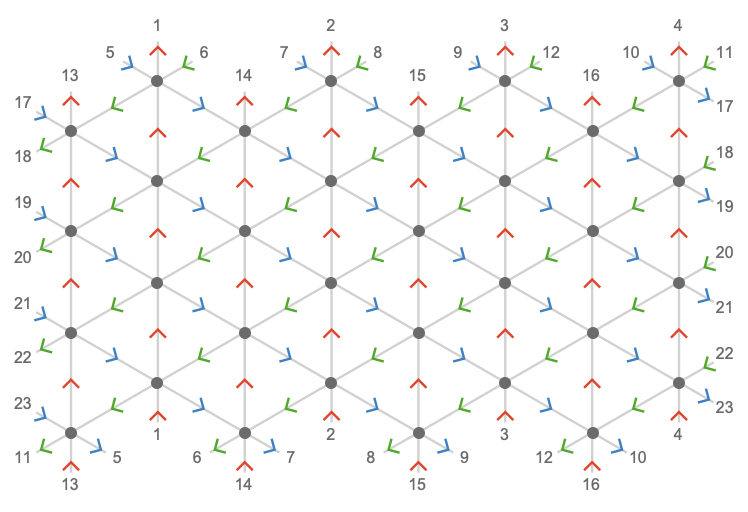
In this case, the dimension 4 measures the number vertices visited before the \( \reFo{\card{r}} \)-axis loops back to itself, and similarly 8 measures this count for the \( \grFo{\card{g}} \)-axis (and also the \( \blFo{\card{b}} \)-axis):
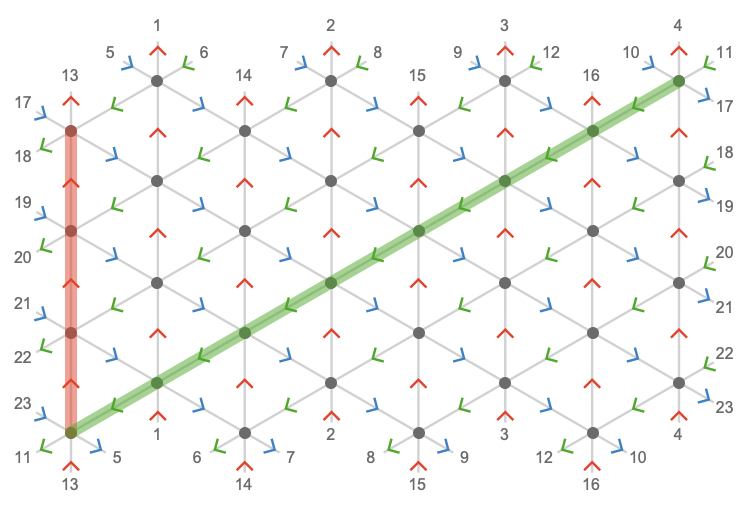
Here we visualize the triangular torus in 3 dimensions:
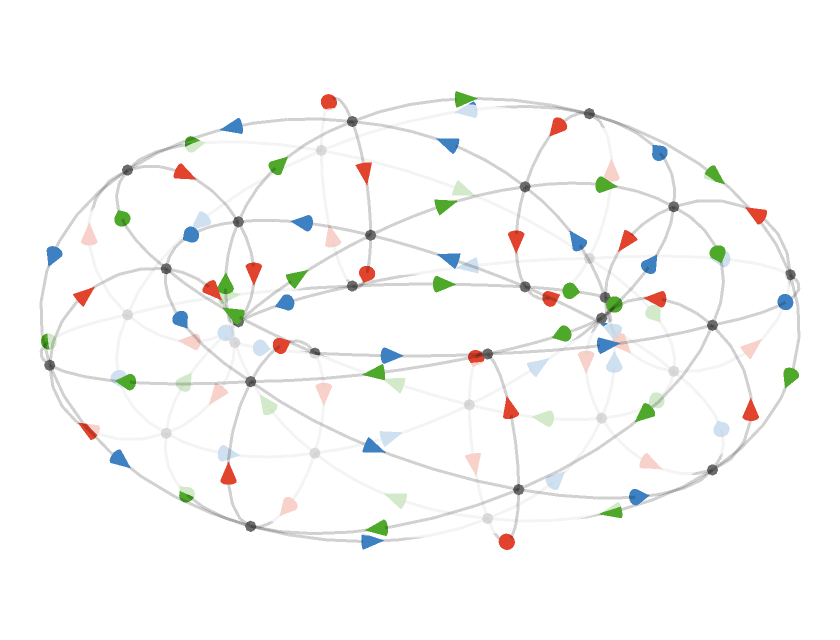
We can highlight the cardinal axes:
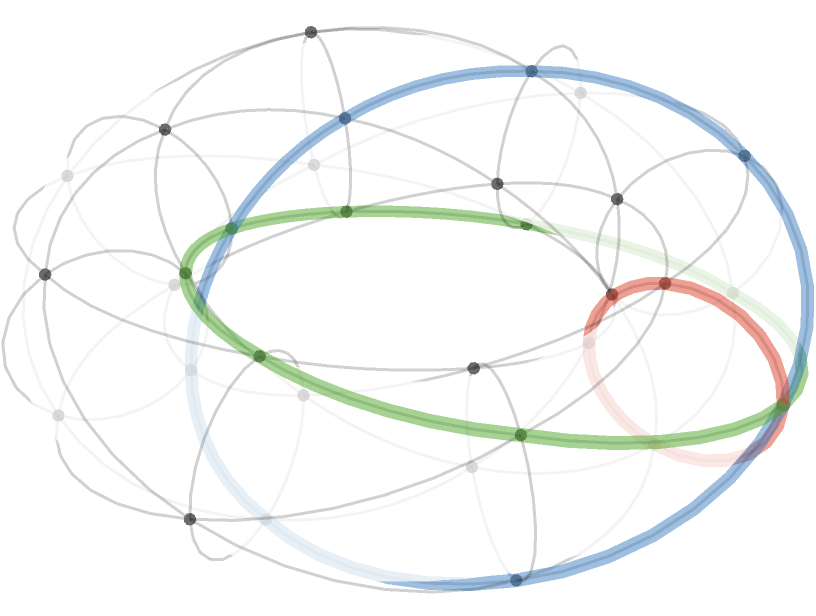
Triangular cylinder #
Here is (a fragment of) the triangular cylinder \( \bindCardSize{\triangularQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{4},\grFo{\card{g}}\compactBindingRuleSymbol \infty ,\blFo{\card{b}}\compactBindingRuleSymbol \infty } \), cyclic in the \( \reFo{\card{r}} \) dimension but infinite in the \( \grFo{\card{g}} \) and \( \blFo{\card{b}} \) dimensions:
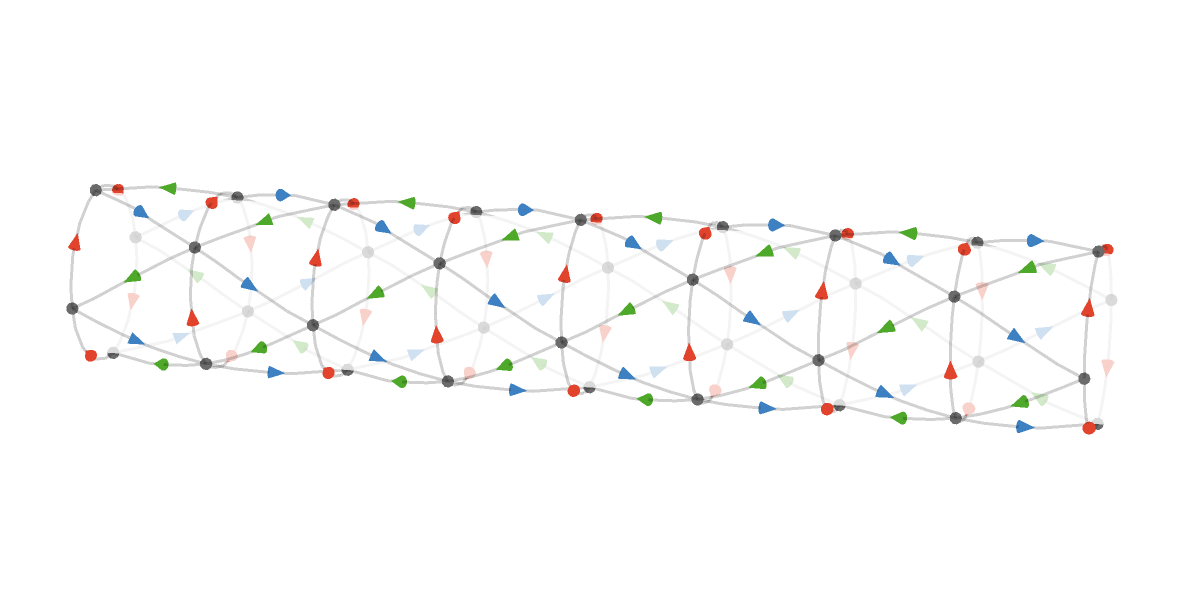
Also note that we are using an artificial transparency effect to make the three dimensional structure easier to perceive.
Hexagonal torus #
Having established the construction of the triangular torus, we can produce the hexagonal torus by adjusting the fundamental quiver from \( \quiver{F} = \bindCardSize{\bouquetQuiver{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \) to \( \quiver{F} = \bindCardSize{\subSize{\lineQuiver }{2}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}\parallelCardSymbol \blFo{\card{b}}} \) as we explored in Intransitive lattices.
Here we plot \( \bindCardSize{\toroidalModifier{\hexagonalQuiver }}{\reFo{\card{r}}\compactBindingRuleSymbol 6,\grFo{\card{g}}\compactBindingRuleSymbol 12,\blFo{\card{b}}\compactBindingRuleSymbol 12}\congruentSymbol \bindCardSize{\hexagonalQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{6},\grFo{\card{g}}\compactBindingRuleSymbol \modulo{12},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{12}} \) on the modular plane:
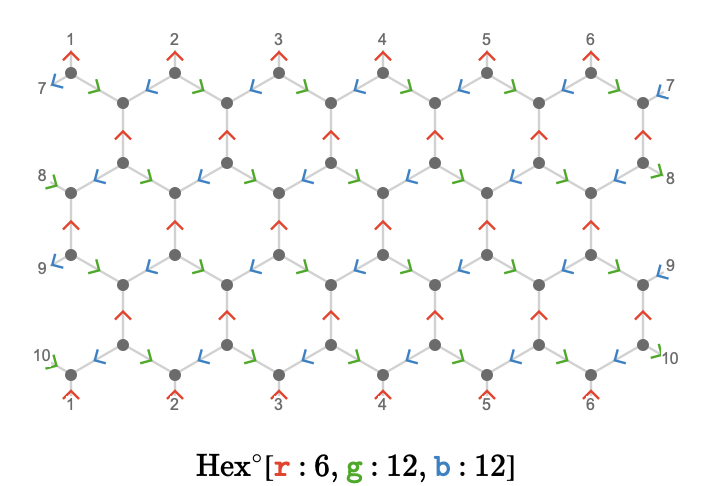
Comparing this to the triangular torus \( \bindCardSize{\triangularQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{6},\grFo{\card{g}}\compactBindingRuleSymbol \modulo{6},\blFo{\card{b}}\compactBindingRuleSymbol \modulo{6}} \), we see that we have can obtain the hexagonal torus by deleting from the triangular torus a periodic pattern of vertices, corresponding to the "forbidden states" that the structure of the fundamental quiver prevents us from visiting:

Three dimensions #
We can plot the torus in three dimensions. Here we show \( \bindCardSize{\toroidalModifier{\hexagonalQuiver }}{\reFo{\card{r}}\compactBindingRuleSymbol 18,\grFo{\card{g}}\compactBindingRuleSymbol 48,\blFo{\card{b}}\compactBindingRuleSymbol 48} \):
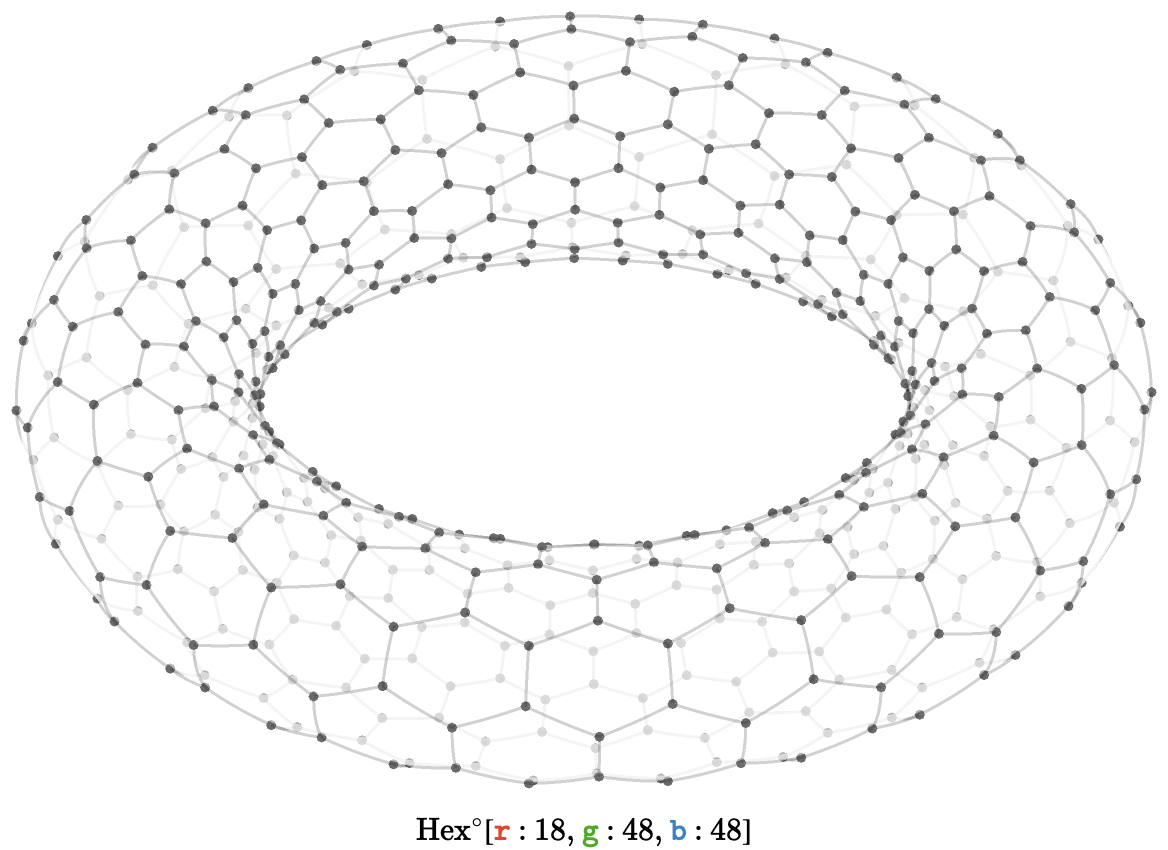
Hexagonal cylinder #
A hexagonal cylinder gives a structure corresponding to the bond connectivity of a carbon nanotube. Here we show \( \bindCardSize{\hexagonalQuiver }{\reFo{\card{r}}\compactBindingRuleSymbol \modulo{12},\grFo{\card{g}}\compactBindingRuleSymbol \infty ,\blFo{\card{b}}\compactBindingRuleSymbol \infty } \):
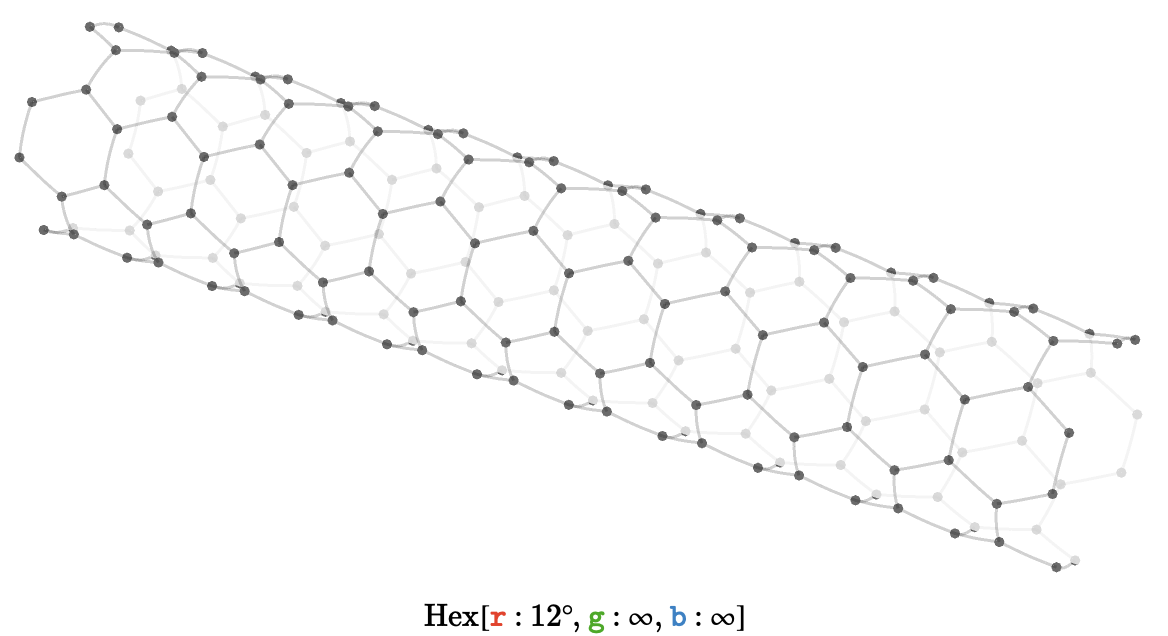
Axes #
Let’s consider for a moment what axis-aligned geodesics look like for toroidal lattices. First, though, let’s consider the situation for the non-toroidal, two-dimensional lattices:
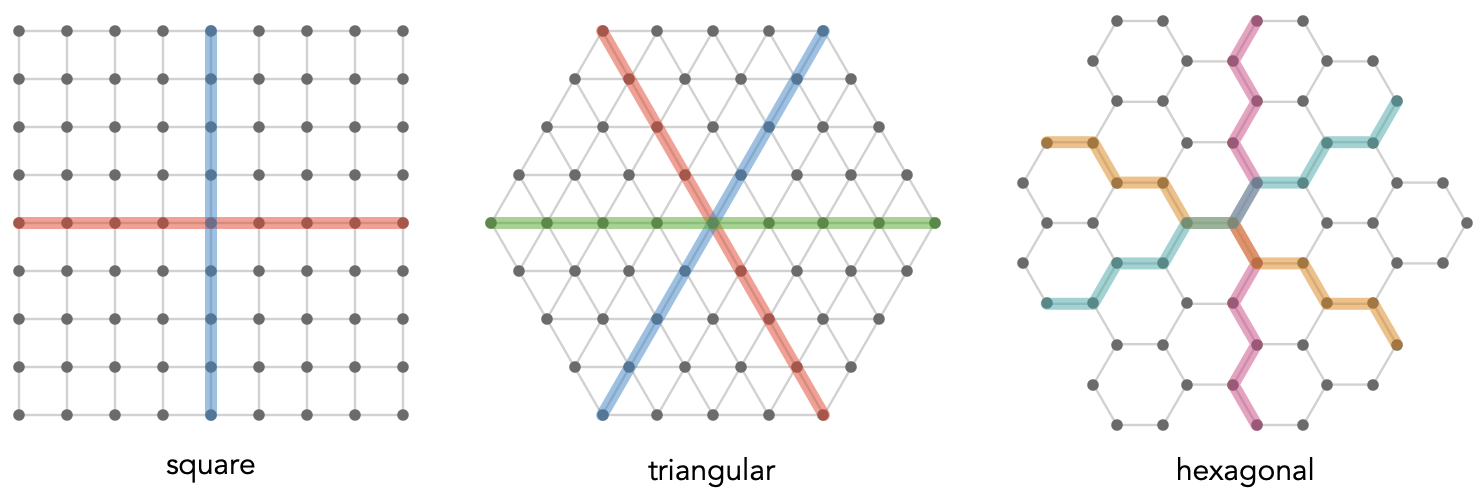
The geodesics are colored by which cardinal they are aligned with. In a hexagonal lattice we cannot form path words like \( \word{\card{a}}{\card{a}}{\card{a}} \), so our “axes” are composed of alternating pairs of cardinals, e.g. \( \word{\card{a}}{\ncard{b}}{\card{a}}{\ncard{b}}{\card{a}}{\ncard{b}} \); we color these paths by blending the colors of the alternated cardinals.
Ok, now we can compare with square torus (top) and triangular torus (bottom):
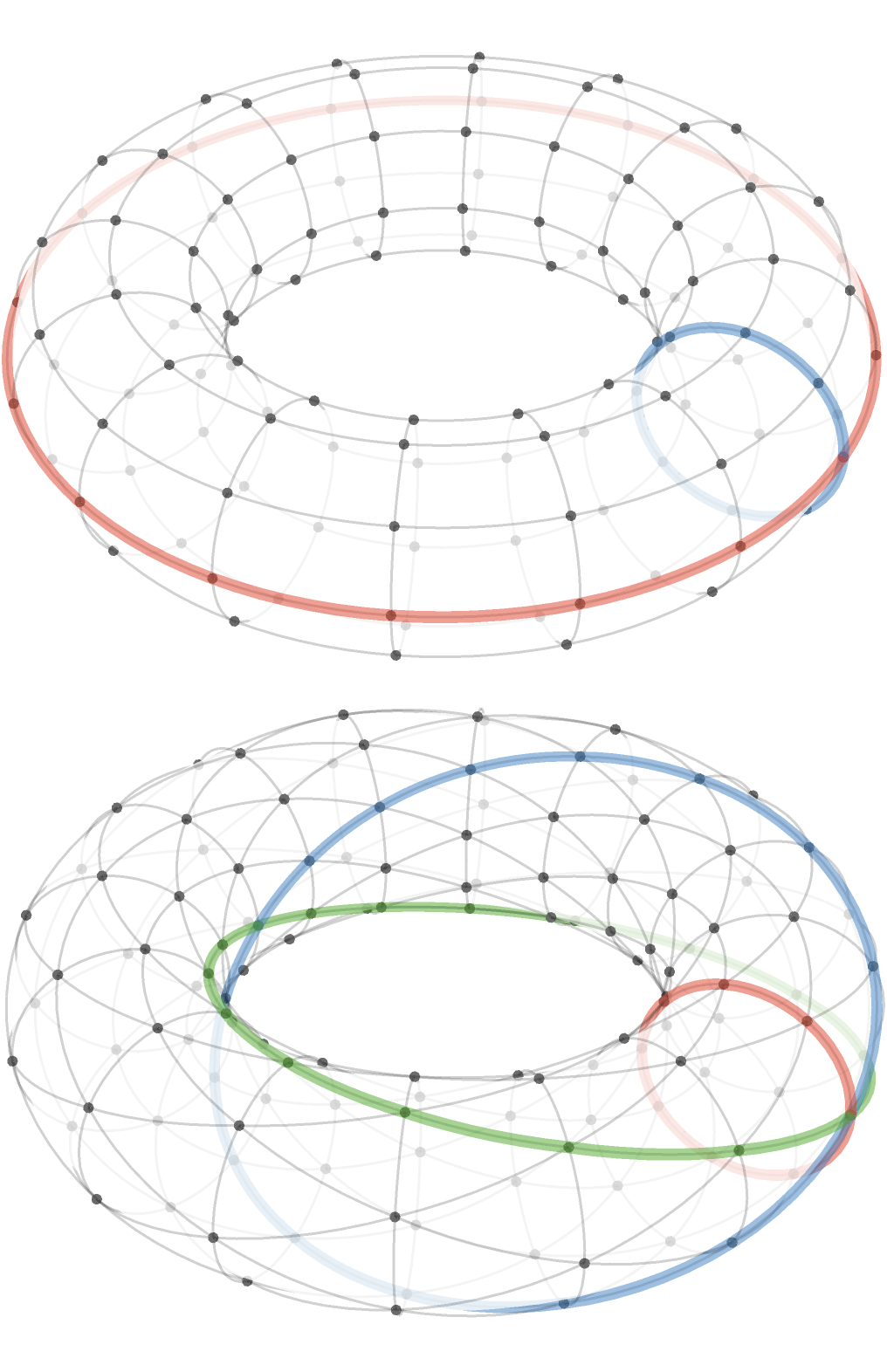
As you probably expected, the square torus has predictable “orthogonal” axes.
But the situation with triangular torus appears to be more interesting: the \( \grFo{\card{g}} \) and \( \blFo{\card{b}} \) axes twist around and meet at an point opposite the origin. This behavior turns out to be sensitive to the moduli of the torus.
If the moduli are coprime, then either of the axes \( \grFo{\card{g}} \) and \( \blFo{\card{b}} \) will reach every vertex:

Modular plane #
This is of course a straightforward consequence of basic number theory, but is best explained by plotting these lattices on the modular plane we introduced earlier. To repeat: we can think of this plane as “wrapping around” on its border -- but we’ll number the edges that cross this border so that it is easy to trace how they connect up:
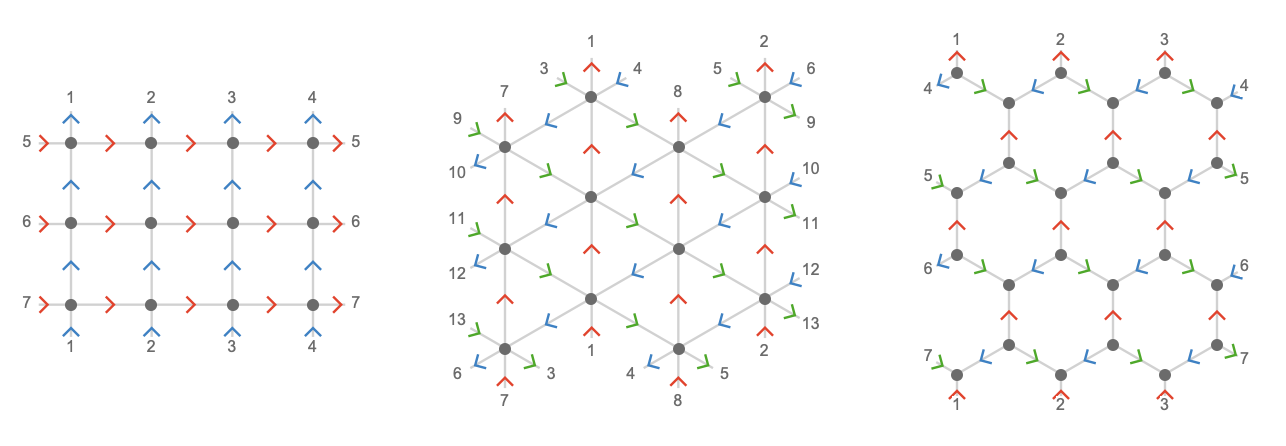
Let’s plot the \( \reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}} \) axes on the plane for \( \bindCardSize{\toroidalModifier{\triangularQuiver }}{\reFo{\card{r}}\compactBindingRuleSymbol 4,\grFo{\card{g}}\compactBindingRuleSymbol 8,\blFo{\card{b}}\compactBindingRuleSymbol 8} \):
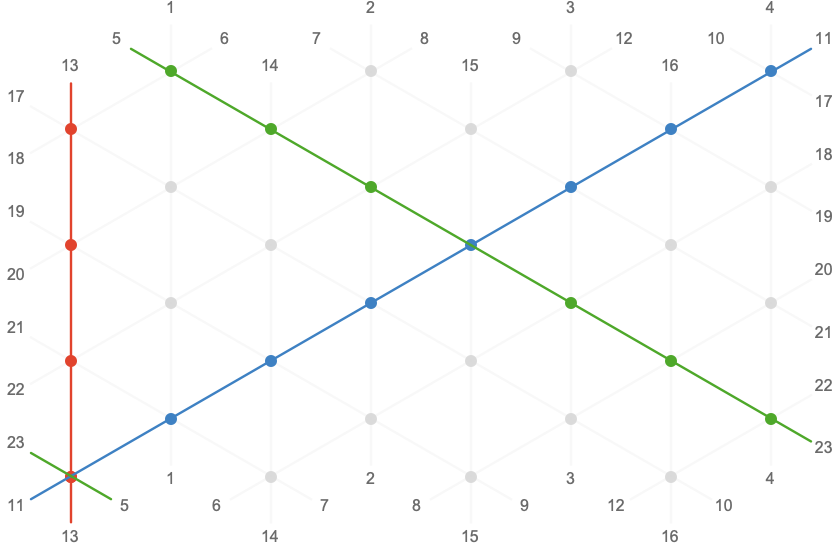
Plotting the \( \reFo{\card{r}} \) and \( \blFo{\card{b}} \) axes for a range of moduli, we can see how the greatest common divisor of the two moduli determines how many orbits of the \( \sym{w} \) dimension the \( \blFo{\card{b}} \) axis will make before returning to the origin:
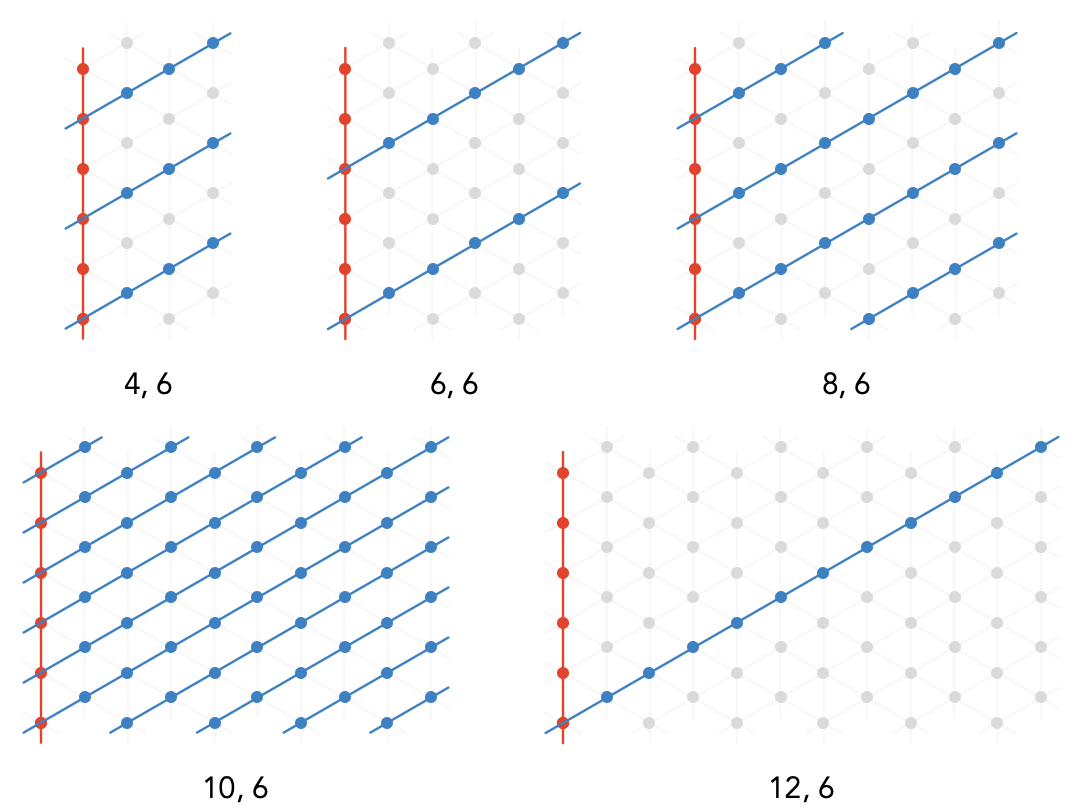
Notice that if \( \sym{w} / 2 \) and \( \sym{h} / 2 \) are coprime, the axis \( \blFo{\card{b}} \) intersects every vertex. In general the number of times \( \reFo{\card{r}} \) will intersect \( \blFo{\card{b}} \) for a \( \sym{w}\times \sym{h} \) torus is \( 2 \, \lcm(\sym{h} / 2,\sym{w}) / \sym{h} \).
A similar situation applies for the hexagonal torus, when we use alternating axes:
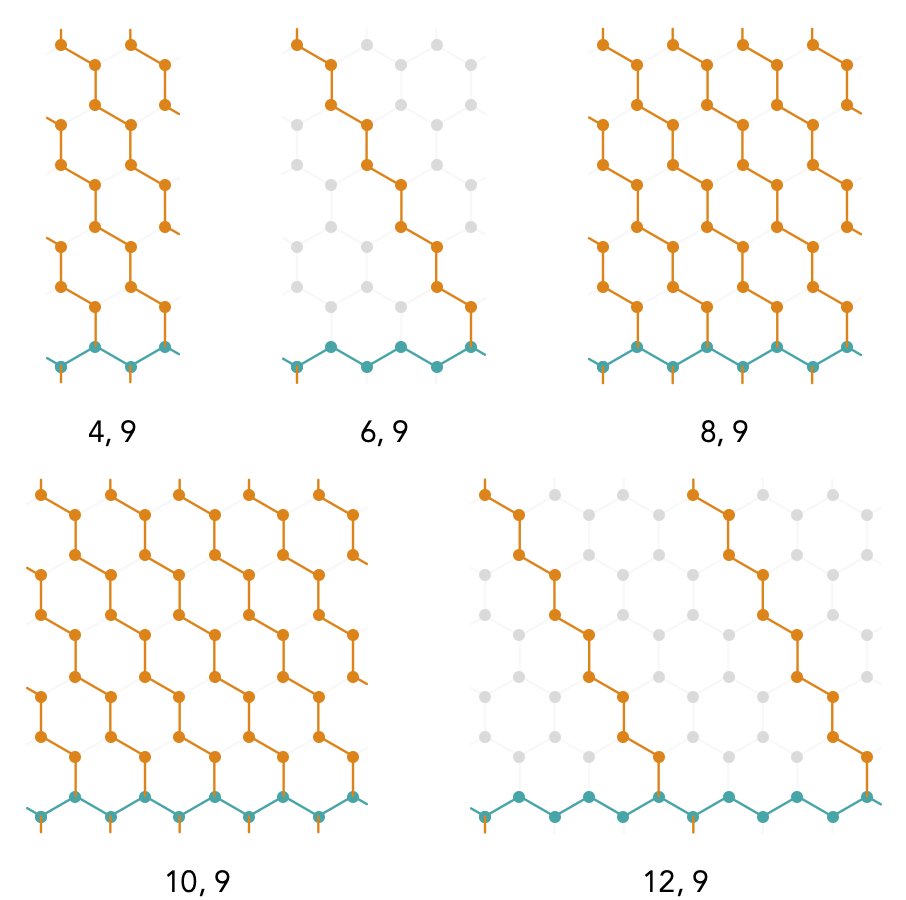
Due to an arbitrary choice of orientation of these hexagons, our previously vertical axis is now horizontal, but a similar relation holds: the number of vertices in the intersection of the axis-aligned geodesics is given by \( 3 \, \lcm(\sym{w},\sym{h} / 3) / \sym{h} \), where it is important to notice the \( \TuFo{\sym{w} = 6, \sym{h} = 9} \) case actually has two such intersecting vertices, not one as it first appears. Similarly the \( \TuFo{\sym{w} = 12, \sym{h} = 9} \) case has 4 intersecting vertices.
We are certainly not limited to these square, triangular, and hexagonal toroidal lattices. Any fundamental quiver employing the same translation groups has a toroidal version. For example, the rhombille lattice:
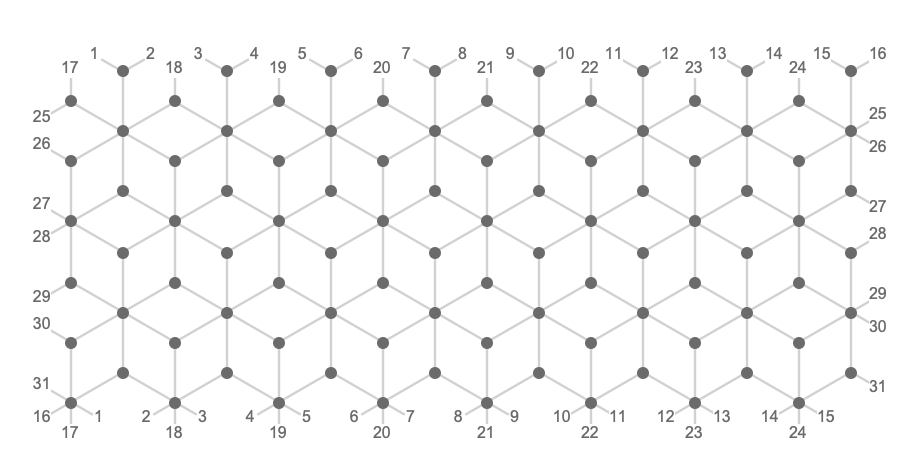
Sheared tori #
There is a straightforward construction we can use to introduce an intuitive kind of shear or torsion into our lattice quivers.
We'll start with the square torus (of size \( 5 \times 3 \)), where the torsion is easiest to see. On the left is the sheared lattice, and on the right is the normal square lattice for comparison.
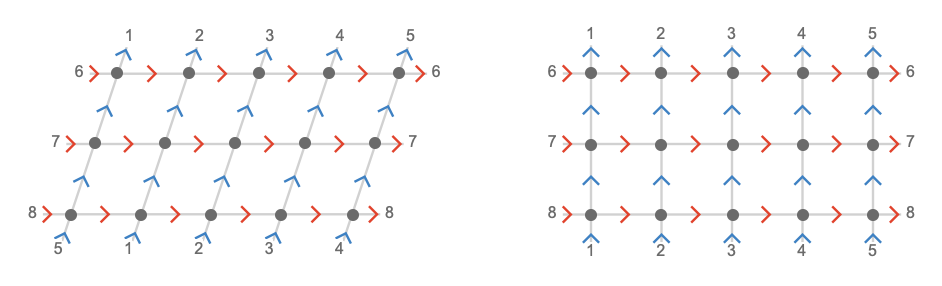
Notice that in the sheared lattice, the top left vertex connects to the second vertex on the bottom left; in the normal lattice it connects to the first. We’ll say that this lattice has a shear parameter of \( \sym{z} = 1 \).
Here are square lattices with shear parameters \( -2 \le \sym{z} \le 2 \):
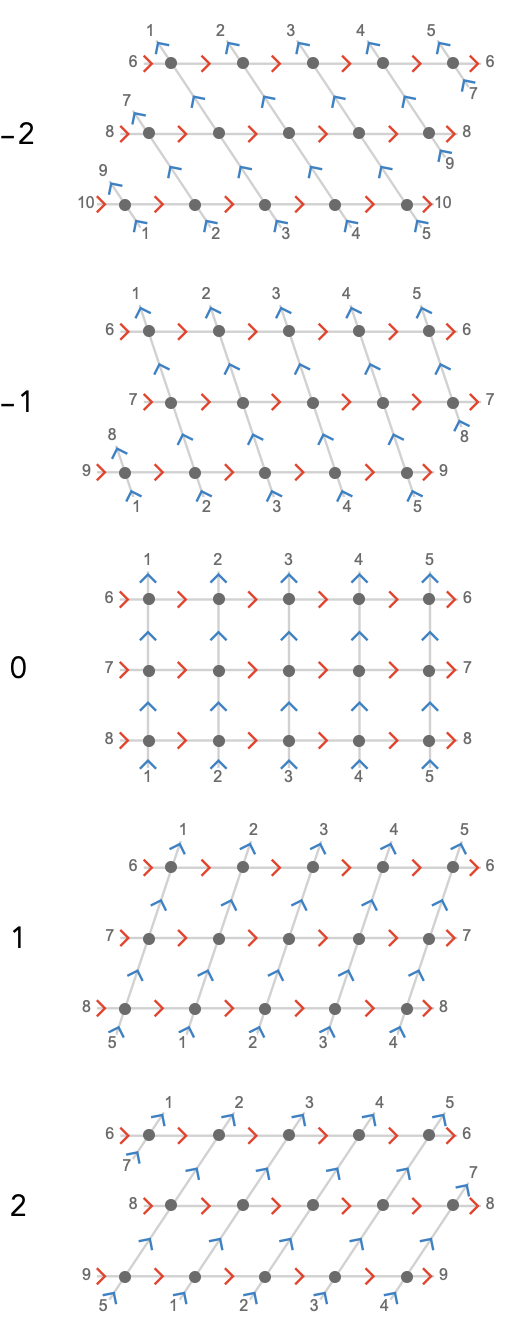
Notice similar "orbital mechanics" for the sheared square lattice as we saw for the triangular lattice: for \( \sym{z} = \pm 1 \), a \( \blFo{\card{y}} \) geodesic will orbit through all vertices, but for \( \sym{z} = \pm 2 \), a \( \blFo{\card{y}} \) geodesic effectively skips the neighboring geodesic on completing a circuit, so if \( \sym{w} \) is even we will have exactly two distinct \( \blFo{\card{y}} \)-orbits.
From a path-algebraic point of view, a \( \sym{z} \)-sheared square lattice can be expressed as the path relation set:
\[ \list{\word{\reFo{\card{x}}}{\blFo{\card{y}}}\pathIso \word{\blFo{\card{y}}}{\reFo{\card{x}}},\repeatedPower{\word{\reFo{\card{x}}}}{\sym{w}}\pathIso \repeatedPower{\word{\blFo{\card{y}}}}{\sym{z}},\repeatedPower{\word{\blFo{\card{y}}}}{\sym{h}}\pathIso \word{1}} \]It's clear then that if \( \sym{z} = \sym{h} \), we have no shear at all, and hence the shear parameter lives in the integers modulo \( \sym{h} \).
When plotted in three dimensions, the twist of a sheared square torus resembles the twisted magnetic field used in a tokamak.