Intransitive lattices #
Introduction #
The lattice quivers we generated in Lattice quivers had the property that their fundamental quivers were bouquet quivers \( \bouquetQuiver{\sym{k}} \), meaning quivers with only one vertex. Since any two paths on a bouquet quiver can be composed, the path groupoid \( \pathGroupoid{\bouquetQuiver{\sym{k}}} \) is isomorphic to word group \( \wordGroup{\quiver{\sym{k}}} \) (the free group on \( \sym{k} \) letters), and the lattice quivers they generate can be seen as Cayley quivers of group presentations of \( \group{\power{\group{\mathbb{Z}}}{\sym{k}}} \) that we named \( \translationPresentation{\sym{k}},\starTranslationPresentation{\sym{k}} \).
By considering fundamental quivers with more than one vertex we can obtain bona-fide path groupoids -- i.e. groupoids that are not groups. This occurs because there will be paths that cannot be composed, namely those pairs \( \path{P},\path{R} \) where \( \headVertex(\path{P}) \neq \tailVertex(\path{R}) \). We’ll see that these produce more complex lattices in which the neighborhoods of vertices are not all alike, even when we generate them to "infinite depth". We'll call these intransitive lattices.
Hexagonal lattice quiver #
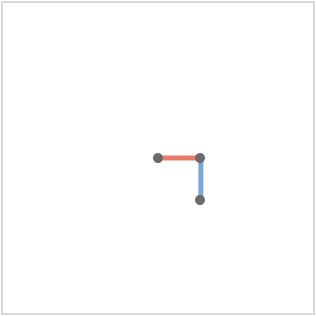
Our first two-vertex fundamental quiver is \( \bindCards{\subSize{\lineQuiver }{2}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}\parallelCardSymbol \blFo{\card{b}}} \), which will generate the hexagonal quiver, which we'll write \( \bindCards{\subSize{\hexagonalQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \). For our path representation we'll use the same homomorphism \( \bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,-1,0}},\mto{\grFo{\card{g}}}{\translationVector{0,1,-1}},\mto{\blFo{\card{b}}}{\translationVector{-1,0,1}}} \), the same homomorphism used to generate the triangular quiver \( \bindCards{\subSize{\triangularQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \). The fundamental quiver and matrix cardinals are shown below:
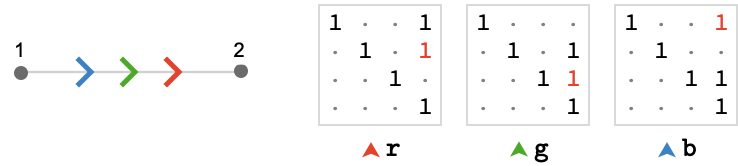
This gives us a hexagonal lattice quiver, shown here to depth 4, starting at fundamental vertex \( \vert{1} \).
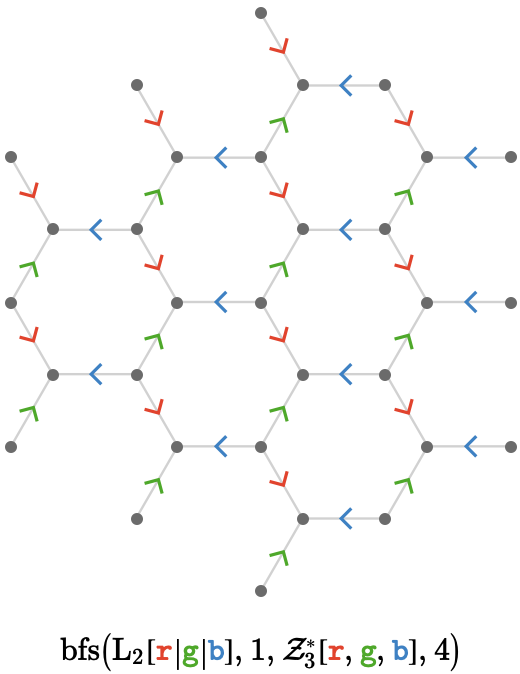
This construction will serve as the definition of the hexagonal lattice quiver:
\[ \bindCardSize{\subSize{\hexagonalQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \compactQuotient{\bindCardSize{\subSize{\lineQuiver }{2}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}\parallelCardSymbol \blFo{\card{b}}}}{1}{\bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}} \]Rhombille lattice quiver #
We can take one obvious step to generalize the previous example: we can extend the fundamental quiver to have 3 vertices: \( \bindCards{\subSize{\lineQuiver }{3}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}\parallelCardSymbol \blFo{\card{b}}} \).
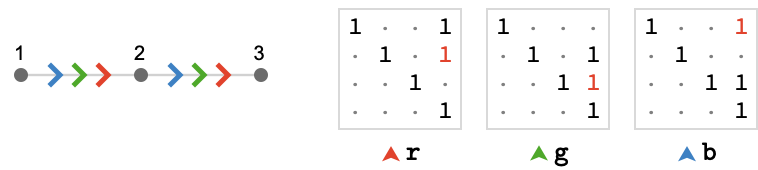
This yields the rhombille lattice \( \bindCards{\subSize{\rhombilleQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}} \), shown here to depth 3, starting at vertex \( \vert{2} \):
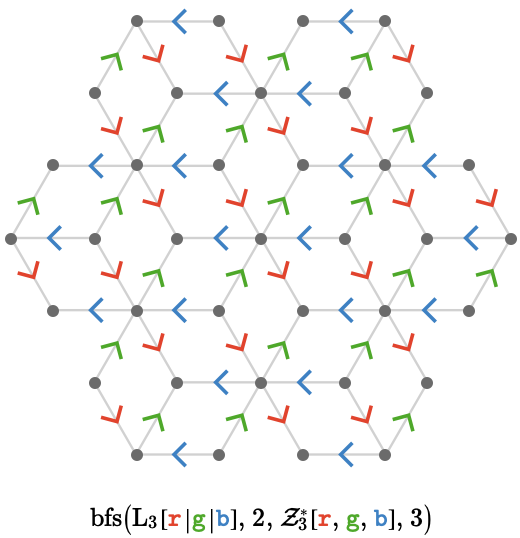
This will serve as the definition of the rhombille lattice quiver:
\[ \bindCardSize{\subSize{\rhombilleQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \compactQuotient{\bindCardSize{\subSize{\lineQuiver }{3}}{\reFo{\card{r}}\parallelCardSymbol \grFo{\card{g}}\parallelCardSymbol \blFo{\card{b}}}}{2}{\bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}} \]Euclidean tilings #
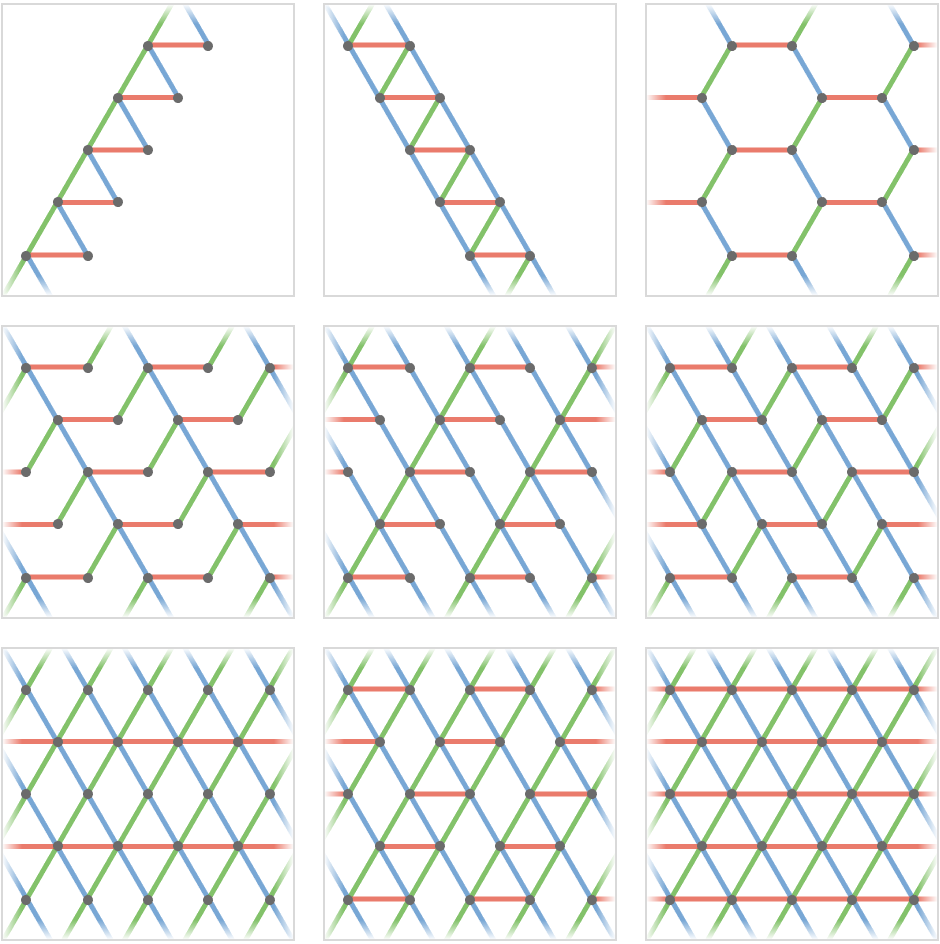
With suitably chosen fundamental quivers and choices of representations, we can generate lattice quivers corresponding to all of the 2D uniform Euclidean tilings. Here are a few of the simpler ones:
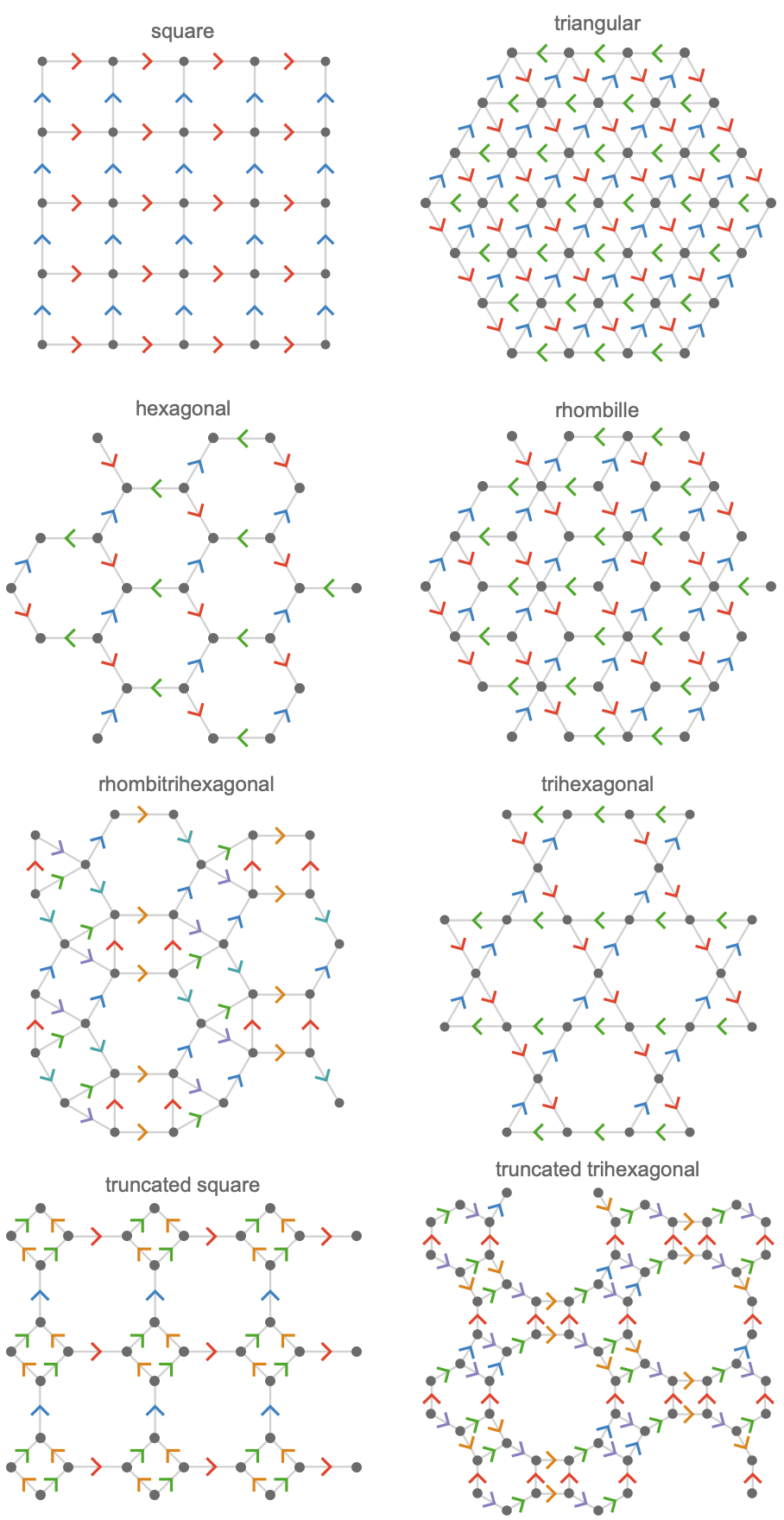
Here are their corresponding quiver representations:
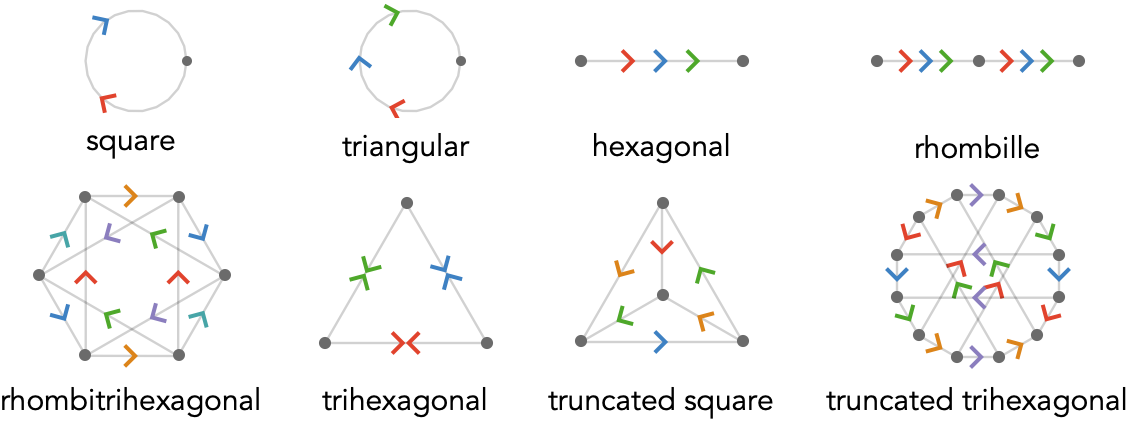
Note that we do not show the associated translation groups here.
Enumeration #
Using the quiver enumeration discussed in Graphs and quivers, it is relatively straightforward to simply enumerate all lattice quivers once we fix a particular group representation, that is, once we fix a particular set of matrices.
2-cardinal lattices #
We'll start with the 9 possible 2-cardinal quivers that we can form on two-vertex skeletons:

We fix the path representation to use \( \translationWordHomomorphism{2} \), the same as that of the square lattice:
\[ \bindCardSize{\translationWordHomomorphism{2}}{\reFo{\card{r}},\blFo{\card{b}}}\defEqualSymbol \assocArray{\mto{\reFo{\card{r}}}{\translationVector{1,0}},\mto{\blFo{\card{b}}}{\translationVector{0,1}}} \]Up to graph isomorphism, we obtain the following 6 lattice quivers:
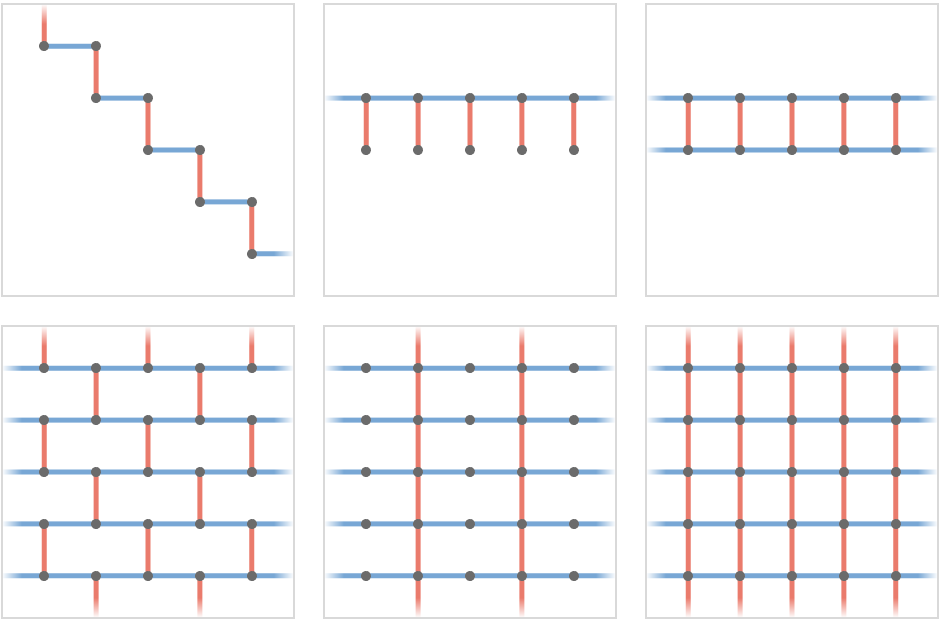
Note that I am deliberately ignoring "self-intersecting" lattices in which contain pairs of states \( \TuFo{\vert{x}, \matrix{M}} \), \( \TuFo{\vert{y}, \matrix{M}} \) with \( \vert{x} \neq \vert{y} \), since these would produce ambiguous 2D layouts when rendered in the natural way.
We now consider the 69 2-cardinal lattices on three vertices, the first 18 of which are shown below:
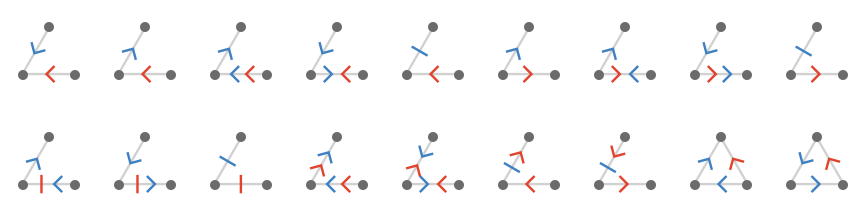
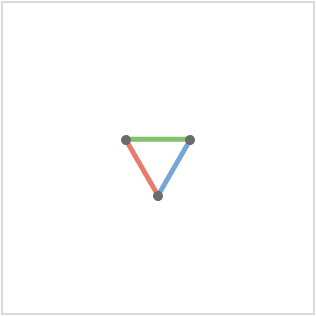
Up to isomorphism, we obtain 18 lattice quivers. One of them is finite, consisting only of three vertices:
Another 9 are again effectively 1-dimensional, being variations of a "tile" that repeats on a band:
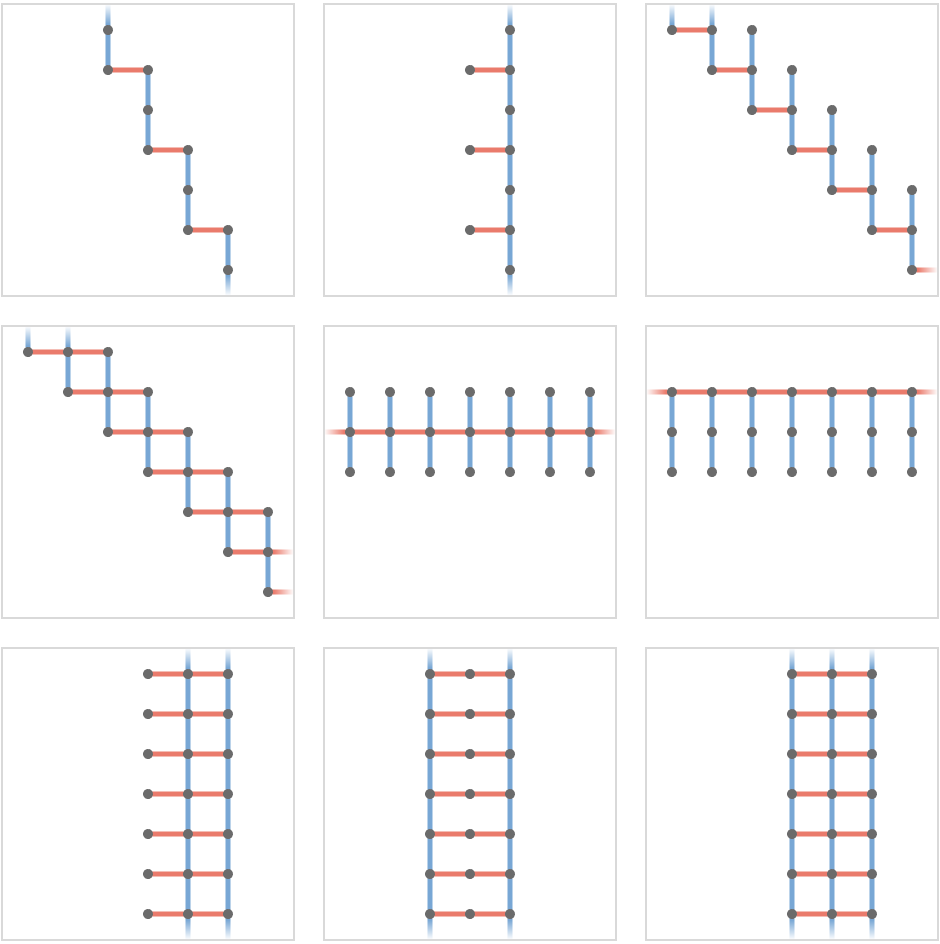
The remaining 8 are 2-dimensional, with a tile that repeats in both dimensions:
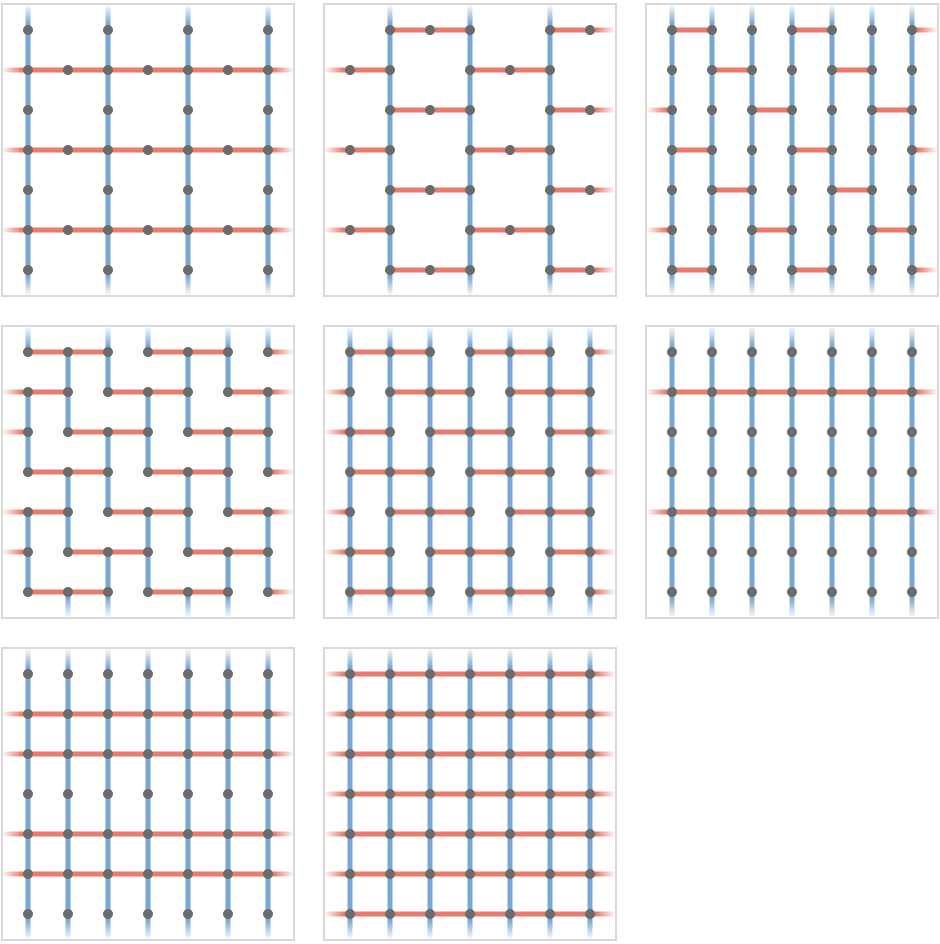
3-cardinal lattices #
Next we'll consider the 26 different 3-cardinal quivers on the skeletons with two vertices:
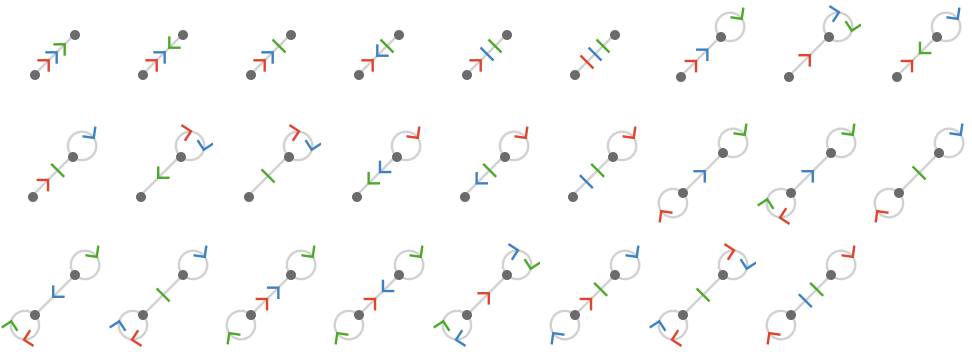
We'll fix the path representation to use \( \starTranslationWordHomomorphism{3} \), that of the triangular lattice, so as to produce two-dimensional quivers:
\[ \bindCardSize{\starTranslationWordHomomorphism{3}}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\defEqualSymbol \homomorphismMapping{\mto{\reFo{\card{r}}}{\translationVector{1,-1,0}},\mto{\grFo{\card{g}}}{\translationVector{0,1,-1}},\mto{\blFo{\card{b}}}{\translationVector{-1,0,1}}} \]Up to isomorphism these generate the following 9 lattice quivers:
Notice we recover the \( \triangularQuiver \) and \( \hexagonalQuiver \), as expected.
For the 1124 different 3-cardinal quiver on skeletons with three vertices, we obtain 80 lattice quivers. One of these is effectively 0-dimensional, being finite:
Another 21 are again effectively 1-dimensional, being variations of a "bar" of maximum width 3 that repeats infinitely:

The remaining 58 are two-dimensional:

Notice that the some of these lattices are the same as those produced by 2-vertex fundamental quivers. Briefly, this is explained by a suitable covering.
Vertex colorings #
Intransitive lattices by definition have "different types of vertex". These "types" naturally lead us to consider colorings of vertices. Let's look at two simple examples:
Hexagonal lattice #
We return to the hexagonal lattice, which we saw had a fundamental quiver with two vertices. Here it is again:
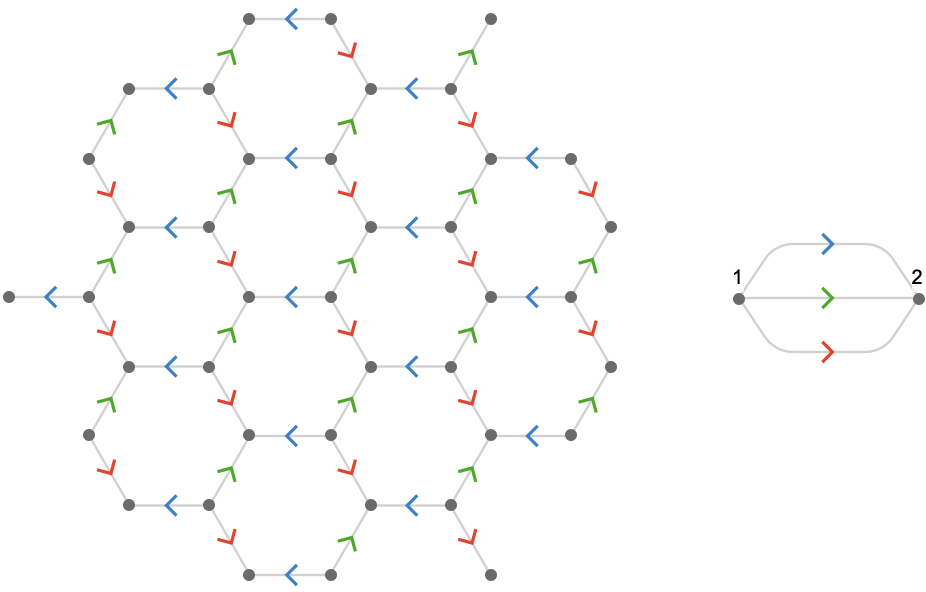
The vertices of this lattice quiver are also of two types, which we could call “outward” and “inward”:
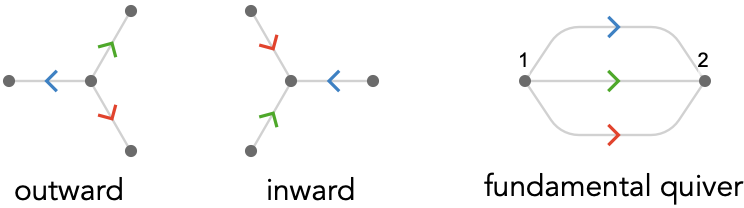
These two types of vertex in the lattice quiver correspond to the vertices labeled 1 and 2 in the fundamental quiver: the cardinals available to vertex 1 are all outgoing, and the cardinals available to vertex 2 are all incoming. This motif is reflected by the outward and inward sets of vertices in the lattice quiver. This correspondence reflects a general and important fact: lattice quivers are covering quivers of their fundamental quivers, as we will explain in the next section.
We can illustrate these two types of vertex visually by coloring the vertices of the lattice quiver by the identity of the vertex that generated them:
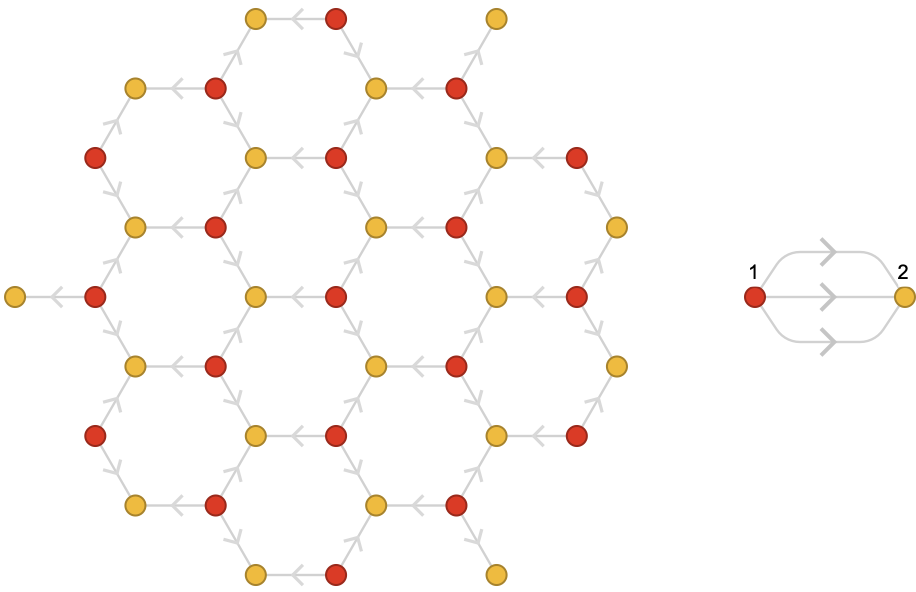
Rhombille lattice #
Now let’s look at the rhombille tiling, which has three types of vertices in its fundamental quiver:
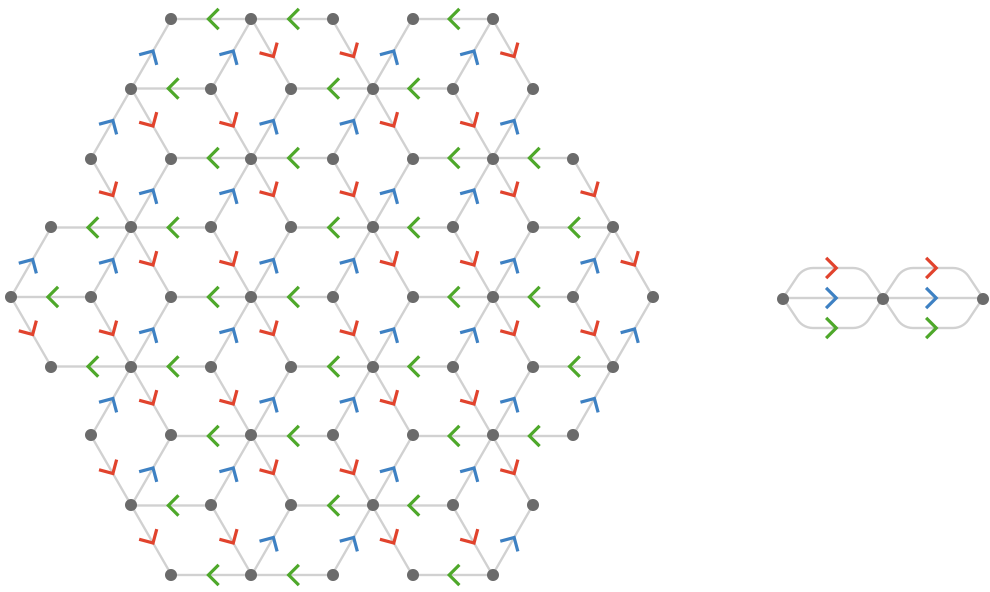
Again, these three vertices correspond to the types of vertex we find in the lattice quiver:

Again, we can color each vertex to indicate which of the three fundamental vertices generated it:
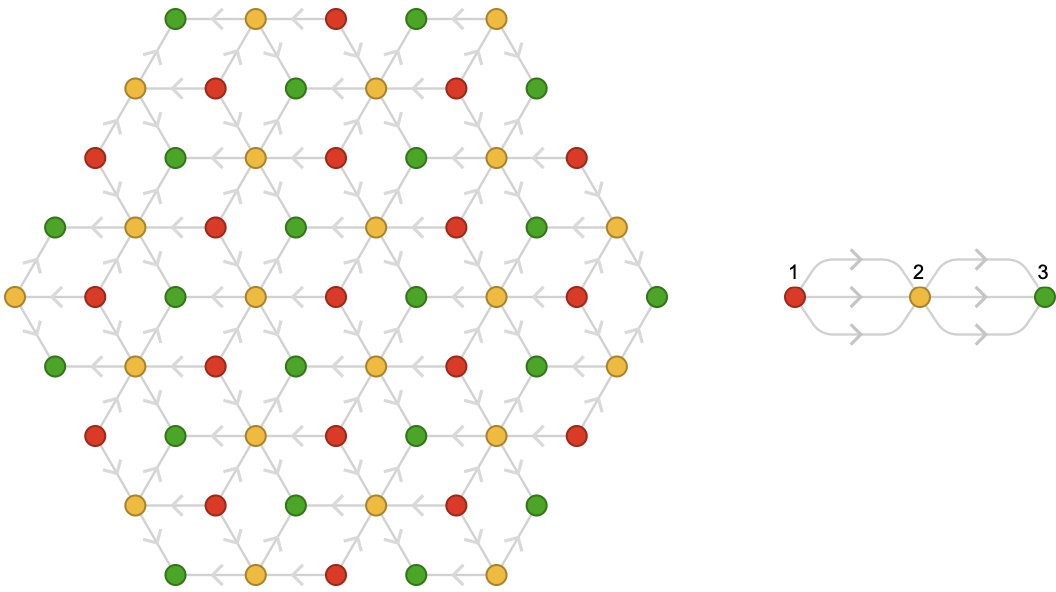
This coloring phenomena is richer than it first appears, and we will address it in more detail in the section Vertex colorings.