Path groupoids #
Path words #
The fundamental object of study in quiver geometry is the path, which is what it sounds like: a journey in the quiver, starting at some particular initial vertex, called the tail vertex, and ending at some final vertex, called the head vertex.
For concrete examples, we'll use the following quiver:
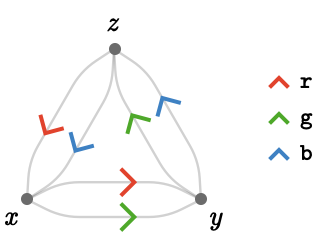
We'll write paths using the notation \( \paren{\pathWord{\vert{tail}}{\word{\card{c}}{\card{a}}{\card{r}}{\card{d}}{\card{i}}{\card{n}}{\card{a}}{\card{l}}{\card{s}}}{\vert{head}}} \), where \( \vert{tail} \) and \( \vert{head} \) are vertices and \( \word{\card{c}}{\card{a}}{\card{r}}{\card{d}}{\card{i}}{\card{n}}{\card{a}}{\card{l}}{\card{s}} \) is a path word: a sequence of cardinals. The parentheses are optional and are added for clarity. Here are some examples to make the idea clear:
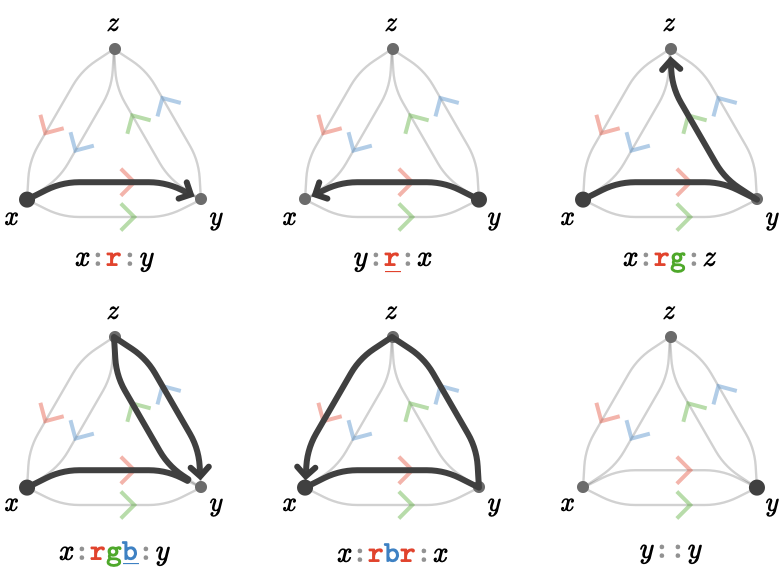
Notice in the second and fourth examples: when we traverse an edge in the opposite direction to its associated cardinal e.g. \( \reFo{\card{r}} \), we record this cardinal in the path word inverted, written with an underbar \( \reFo{\inverted{\card{r}}} \).
Our priority will be to describe how to compose paths, and how this behavior yields a path groupoid.
Path operations #
Path composition #
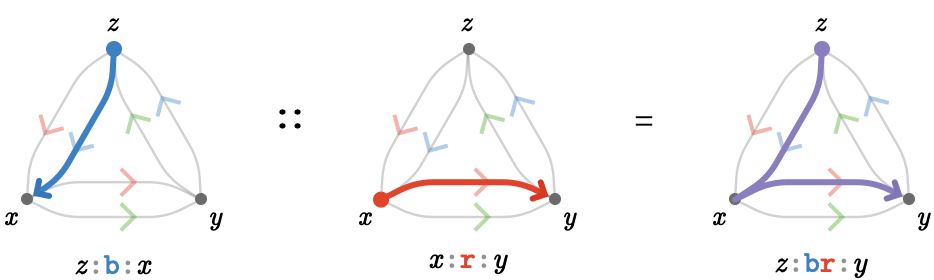
There is a natural operation we can perform to combine two paths \( \path{P} \) and \( \path{R} \): we can compose them "head-to-tail".
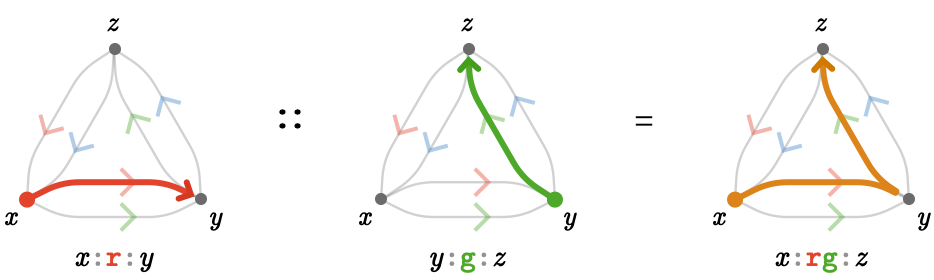
We'll call this path composition, which we'll write \( \pathCompose{\path{P}}{\path{R}} \) and pronounce "\( \path{P} \) composed with \( \path{R} \)". It behaves word-algebraically as:
\[ \pathCompose{\paren{\pathWord{\vert{x}}{\wordSymbol{P}}{\vert{y}}}}{\paren{\pathWord{\vert{y}}{\wordSymbol{R}}{\vert{z}}}} = \parenPathWord{\vert{x}}{\concat{\wordSymbol{P} \wordSymbol{R}}}{\vert{z}} \]We'll now perform the composition \( \pathCompose{\paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}}{\vert{y}}}}{\paren{\pathWord{\vert{y}}{\word{\grFo{\card{g}}}}{\vert{z}}}} \) to give \( \paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}{\grFo{\card{g}}}}{\vert{z}}} \):
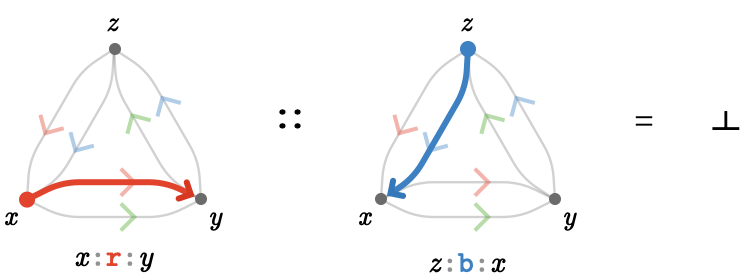
As an example of a multiplication that is not defined, consider \( \pathCompose{\paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}}{\vert{y}}}}{\paren{\pathWord{\vert{z}}{\word{\blFo{\card{b}}}}{\vert{x}}}} \). The first path ends at a different vertex from where the second path starts (\( \vert{y} \neq \vert{z} \)), so we cannot form a composite path.
We indicate this with the null result, written \( \nullPath \).
We can however compose these paths in the reverse order:
This should make it clear, if it wasn’t already, that path composition is not a commutative operation.
Inversion #
We define the inverse of a path \( \path{P} \), written \( \inverted{\path{P}} \) or \( \inverse{\path{P}} \), to be the path followed in the opposite direction.
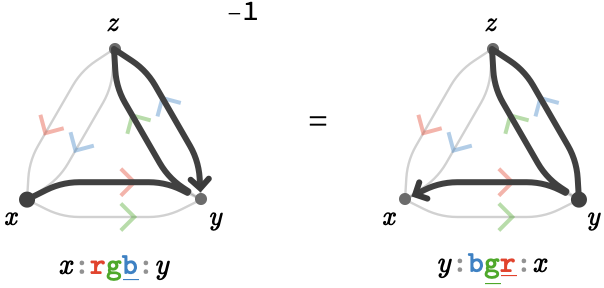
Notice that the cardinals of the path word are simultaneously reversed and inverted.
Empty paths #
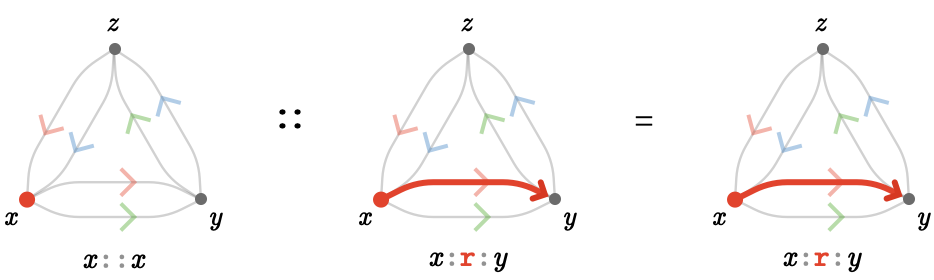
It is important to emphasize that empty paths serve a crucial role, since they behave like identity elements the leave paths unchanged under composition.
For example, we can left-multiply any path having tail vertex \( \vert{x} \) with the empty path \( \groupoidIdentityElement{1}{\vert{x}} = \parenPathWord{\vert{x}}{\emptyWord{}}{\vert{x}} \).
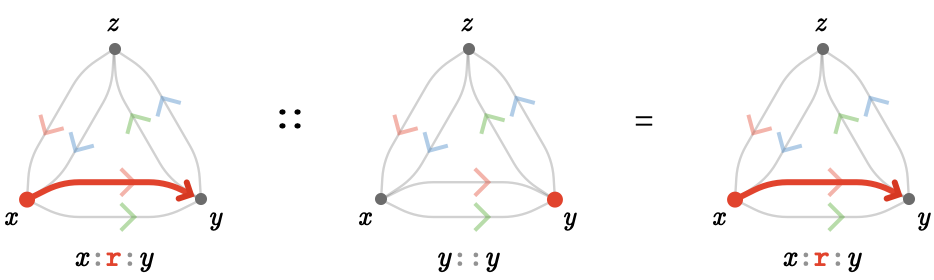
Similarly we can right-multiply any path with head vertex \( \vert{y} \) with the empty path \( \identityElement{y} \):
Loosely speaking, the inverse of an element is something that multiplies with it to produce an identity element. It should be clear that inverse of a path, when composed with it on the left or right, yields the empty path on its tail or head respectively.
Algebraically, \( \pathCompose{\path{P}}{\inverse{\path{P}}} = \groupoidIdentityElement{1}{\vert{t}},\pathCompose{\inverse{\path{P}}}{\path{P}} = \groupoidIdentityElement{1}{\vert{h}} \), where \( \groupoidIdentityElement{1}{\vert{t}} \) and \( \groupoidIdentityElement{1}{\vert{h}} \) are the empty paths at the tail vertex \( \vert{t} \) and head vertex \( \vert{h} \) of \( \path{P} \):
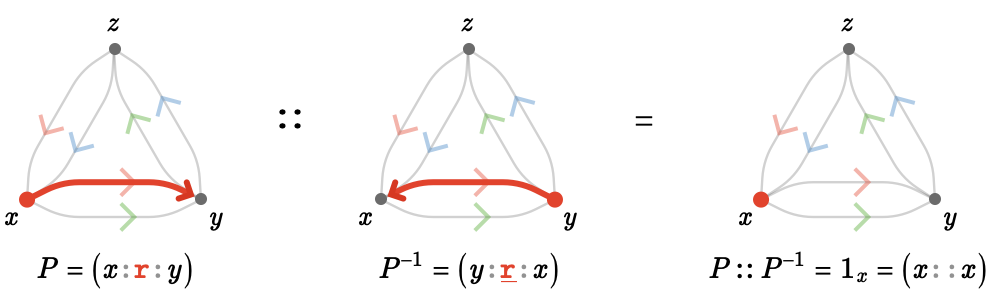
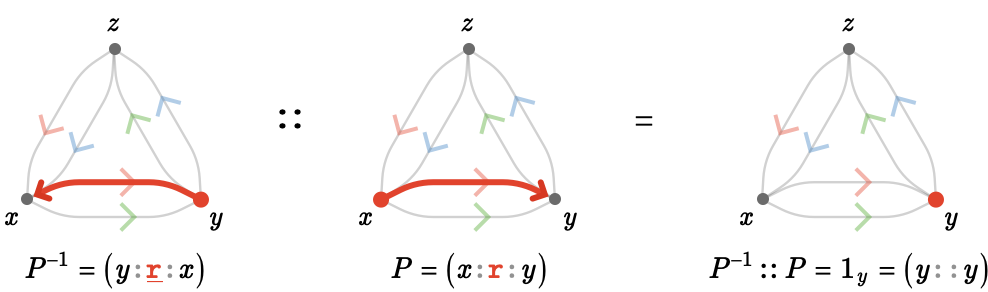
Cancellation #
We’ve seen above that we cancel backtracking paths when composing:
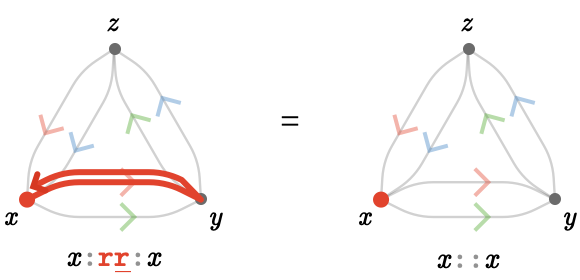
Here's a more complex example:
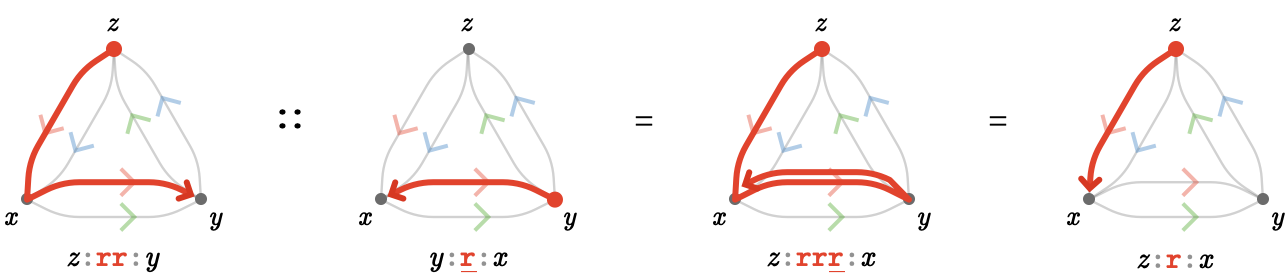
When operating at the level of path words, we performed the word simplification \( \concat{\reFo{\card{r}} \reFo{\inverted{\card{r}}}} = 1 \) in the first case and \( \concat{\reFo{\card{r}} \reFo{\card{r}} \reFo{\inverted{\card{r}}}} = \reFo{\card{r}} \) in the second case. The symbol \( "1" \) here refers to the empty word, which is otherwise hard to indicate.
There is in fact only one kind of simplification we can do, which is to cancel neighboring inverted cardinals: \( \rewrite{\concat{\wordSymbol{L} \inverted{\card{c}} \card{c} \wordSymbol{R}}}{\concat{\wordSymbol{L} \wordSymbol{R}}},\rewrite{\concat{\wordSymbol{L} \card{c} \inverted{\card{c}} \wordSymbol{R}}}{\concat{\wordSymbol{L} \wordSymbol{R}}} \), where \( \wordSymbol{L} \) and \( \wordSymbol{R} \) stand for any sub-words consisting of zero or more cardinals.
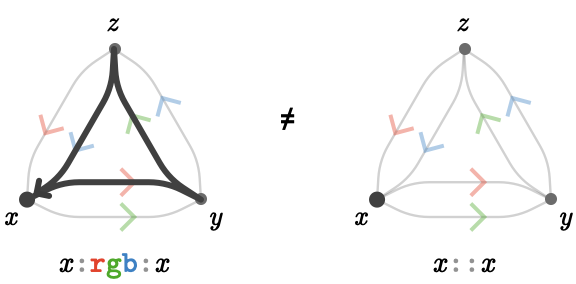
But while the path word \( \concat{\card{c} \inverted{\card{c}}} \) represents a trivial loop in some sense, it is crucial we do not cancel sub words corresponding to non-trivial loops that involve more than one cardinal:
Path groupoid #
Groups and groupoids #
Let's recall the elementary notions of a group and a groupoid.
A group is a structure \( \TuFo{\group{G}, \Gmult } \) consisting of a set of elements \( \group{G} \) and a multiplication \( \functionSignature{\function{\Gmult }}{\TuFo{\group{G}, \group{G}}}{\group{G}} \). The multiplication is associative, so \( \groupElement{f}\Gmult \paren{\groupElement{g}\Gmult \groupElement{h}} = \paren{\groupElement{f}\Gmult \groupElement{g}}\Gmult \groupElement{h} \) for all \( \elemOf{\groupElement{f},\groupElement{g},\groupElement{h}}{\group{G}} \). Each element \( \groupElement{g} \) also has an inverse \( \groupInverse{\groupElement{g}} \) satisfying \( \groupInverse{\groupElement{g}}\Gmult \groupElement{g} = \groupElement{g}\Gmult \groupInverse{\groupElement{g}} = \groupIdentity{e} \), where the property \( \groupIdentity{e}\Gmult \groupElement{g} = \groupElement{g}\Gmult \groupIdentity{e} = \groupElement{g} \) defines the unique identity or unit element \( \elemOf{\groupElement{e}}{\group{G}} \).
A groupoid is, roughly speaking, a group in which the multiplication \( \Gmult \) becomes a partial function, and so need not be defined for all pairs \( \elemOf{\groupoidElement{g},\groupoidElement{h}}{\groupoid{G}} \). Importantly, a groupoid does not need to have a unique identity: in general, there can be multiple identity elements that satisfy the required properties for different subsets of \( G \). We'll call these the units of the groupoid.
Path groupoid #
It is easy to check that the set of finite paths \( \pathList(\quiver{Q}) \) of a cardinal quiver \( \quiver{Q} \) and the operations \( \pathComposeSymbol{} \) and \( \pathReverse{\plSqSy} \), together define a path groupoid, written \( \pathGroupoid{\quiver{Q}} \), that describes how paths compose. The units of the path groupoid is the set \( \setConstructor{\groupoidIdentityElement{1}{\vert{v}}\syntaxEqualSymbol \parenPathWord{\vert{v}}{\emptyWord{}}{\vert{v}}}{\elemOf{\vert{v}}{\graph{G}}} \) of empty paths on the vertices of the quiver, and the inverse of a path is the reversal of that path. As you'd expect, when two paths are not head-to-tail and so cannot be composed, the groupoid multiplication \( \pathComposeSymbol{} \) between them is undefined.