Quiver products #
Motivation #
In this section we will consider how we can form product spaces in quiver geometry, which we call quiver products: quivers constructed as products of two or more factor quivers. Quiver products will be important in a latter section, where we will need them to define the local trivializations used in fibre bundles, but they'll also give us a new perspective on transitive quivers.
Quiver products #
What is a quiver product? Speaking informally, a quiver product between two quivers \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) is another quiver \( \quiver{\piFo{Q}} \) with the following properties:
\[ \begin{aligned} \vertexList(\quiver{\piFo{Q}})&= \vertexList(\quiver{\reFo{R}})\cartesianProductSymbol \vertexList(\quiver{\blFo{S}})\\ \edgeList(\quiver{\piFo{Q}})&\subseteq \pathList(\quiver{\reFo{R}})\cartesianProductSymbol \pathList(\quiver{\blFo{S}})\end{aligned} \]There are many possible products \( \quiver{\piFo{Q}} \), corresponding to systematic ways to choose the subsets of the Cartesian product \( \pathList(\quiver{\reFo{R}})\cartesianProductSymbol \pathList(\quiver{\blFo{S}}) \). We will gradually introduce the formalism to do this.
Of course, we must also attach a cardinal structure to the product \( \quiver{\piFo{Q}} \), defining how the so-called product cardinals label its edges.
Terminology #
To talk clearly about the vertices, edges, and cardinals of \( \quiver{\piFo{Q}} \), and contrast them with the vertices, edges, and cardinals of \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \), we will use the following terms:
| z | z |
|---|---|
| factor quiver | \( \quiver{\reFo{R}} \) or \( \quiver{\blFo{S}} \) |
| factor vertex | vertex of \( \quiver{\reFo{R}} \) or \( \quiver{\blFo{S}} \) |
| factor transition | path in \( \quiver{\reFo{R}} \) or \( \quiver{\blFo{S}} \) |
| factor cardinal | cardinal of \( \quiver{\reFo{R}} \) or \( \quiver{\blFo{S}} \) |
These ingredients will be combined to form the vertices, edges, and cardinals of \( \quiver{\piFo{Q}} \), as follows:
| z | z | z |
|---|---|---|
| product quiver | \( \quiver{\piFo{Q}} \) | constructed from factor quivers |
| product vertex | vertex of \( \quiver{\piFo{Q}} \) | constructed from tuples of factor vertices |
| product cardinal | cardinal of \( \quiver{\piFo{Q}} \) | constructed from tuples of factor transitions |
We will use \( \vertexProduct{\vert{\reFo{u}},\vert{\blFo{v}}} \) to represent the product vertex consisting of factor vertices \( \vert{\reFo{u}} \) and \( \vert{\blFo{v}} \) from factor quivers \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \), and similarly \( \cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}} \) to represent the product cardinal consisting of factor cardinals \( \reFo{\card{r}} \) and \( \blFo{\card{b}} \).
Color #
To ease the notational burden and avoid unnecessary use of subscripts, we'll use color to associate vertices, edges, and cardinals with their corresponding graphs in a product. For example, for quivers \( \quiver{\reFo{R}},\quiver{\blFo{S}} \) we'll refer generically to particular vertices belonging to \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) with symbols \( \vert{\reFo{r}} \) and \( \vert{\blFo{s}} \). Likewise we'll refer to particulars edges with \( \edge{\reFo{e}},\edge{\blFo{f}} \) , and refer to particular cardinals with \( \card{\reFo{c}},\card{\blFo{d}} \).
We'll also use color to relate the product vertices with factor vertices, similar to the role of color in our explanation of coverings. Using this convention the product vertex such as \( \vertexProduct{\vert{\reFo{\fiToSy}},\vert{\grFo{\fiToSy}}} \) is displayed as the additive color blend of the two factor vertex colors, giving \( \vert{\teFo{\fiToSy}} \). Similarly, the product cardinal \( \cardinalProduct{\reFo{\card{r}},\grFo{\card{g}}} \) will be displayed with the colored arrowhead \( \teFo{\arSy} \).
Transitions #
We will now define a large family of binary quiver products by choosing how to combine transitions in the factor quivers \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) into product edges. Transitions in the factor quivers are paths, rather than edges. For the products defined in this section, we will consider paths of maximal length 1.
As we stated above , the vertices of \( \quiver{\piFo{P}} \) are all the possible pairs \( \vertexProduct{\vert{\reFo{u}},\vert{\blFo{v}}} \), where \( \vert{\reFo{u}} \) is a vertex from \( \quiver{\reFo{R}} \) and \( \vert{\blFo{s}} \) is a vertex from \( \quiver{\blFo{S}} \).
Our only freedom in defining a product then comes from how we construct the edges of \( \quiver{\piFo{P}} \) from the paths in \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \), which we will call transitions. We will construct product edges from pairs of transitions from \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \), where we can restrict each the \( \quiver{\reFo{R}} \)-transition and \( \quiver{\blFo{S}} \)-transition to one of three types: forward, backward, and neutral:
-
A forward \( \quiver{\reFo{R}} \)-transition is a 1-path in \( \quiver{\reFo{R}} \) containing a forward (non-inverted) cardinal \( \reFo{\card{r}} \).
-
A backward \( \quiver{\reFo{R}} \)-transition is a 1-path in \( \quiver{\reFo{R}} \) containing a backward (inverted) cardinal \( \reFo{\inverted{\card{r}}} \).
-
A neutral \( \quiver{\reFo{R}} \)-transition is a 0-path in \( \quiver{\reFo{R}} \), labeled with the special factor cardinal \( \reFo{\card{1}} \) that is not part of the cardinal set of \( \quiver{\reFo{R}} \).
The same definitions are used for \( \quiver{\blFo{S}} \)-transitions, of course.
Here are the 9 possible product edges we can form that correspond to pairs of these transitions. These will form the primitive constructors that will generate the edges of the quiver product. Any combinations of these constructors will yield a distinct quiver product.
\[ \begin{csarray}{ccc}{aii} \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{h}}}}{\reFo{\card{r}}}{\blFo{\card{b}}} & \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{b}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{b}}}}{\reFo{\card{r}}}{\blFo{\card{1}}} & \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{h}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{t}}}}{\reFo{\card{r}}}{\blFo{\inverted{\card{b}}}}\\[2em] \mtde{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{h}}}}{\reFo{\card{1}}}{\blFo{\card{b}}} & \mtde{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{b}}}}{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{b}}}}{\reFo{\card{1}}}{\blFo{\card{1}}} & \mtde{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{h}}}}{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{t}}}}{\reFo{\card{1}}}{\blFo{\inverted{\card{b}}}}\\[2em] \mtde{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{h}}}}{\reFo{\inverted{\card{r}}}}{\blFo{\card{b}}} & \mtde{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{b}}}}{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{b}}}}{\reFo{\inverted{\card{r}}}}{\blFo{\card{1}}} & \mtde{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{h}}}}{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{t}}}}{\reFo{\inverted{\card{r}}}}{\blFo{\inverted{\card{b}}}} \end{csarray} \]Here we have laid out the product edges vertically, so that the left and right factors vertices and cardinals now appear on the top and bottom respectively:
\[ \tde{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{t}}}}{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{h}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}}}\syntaxEqualSymbol \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{h}}}}{\reFo{\card{r}}}{\blFo{\card{b}}} \]Let's examine some constructors from this table to understand them better.
The top left entry in the table above is \( \tde{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{t}}}}{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{h}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}}} \), a product edge constructor that combines two factor transitions \( \parenPathWord{\vert{\reFo{t}}}{\reFo{\word{\card{r}}}}{\vert{\reFo{h}}} \) and \( \parenPathWord{\vert{\blFo{t}}}{\blFo{\word{\card{b}}}}{\vert{\blFo{h}}} \). This product edge is labeled with a product cardinal \( \cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}} \) which expresses that these transitions involve forward (non-inverted) cardinals \( \reFo{\card{r}} \) and \( \blFo{\card{b}} \).
The bottom right entry is \( \tde{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{h}}}}{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{t}}}}{\cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\inverted{\card{b}}}}} \), a product edge constructor formed from two factor transitions \( \parenPathWord{\vert{\reFo{h}}}{\reFo{\word{\inverted{\card{r}}}}}{\vert{\reFo{t}}} \) and \( \parenPathWord{\vert{\blFo{h}}}{\blFo{\word{\inverted{\card{b}}}}}{\vert{\blFo{t}}} \), which correspond to edges from \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) that have been traversed backwards. Again, the product cardinal \( \cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\inverted{\card{b}}}} \) expresses this fact.
Now consider the top-right entry \( \tde{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{h}}}}{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{t}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\inverted{\card{b}}}}} \). Here we have a forward factor transition \( \parenPathWord{\vert{\reFo{t}}}{\reFo{\word{\card{r}}}}{\vert{\reFo{h}}} \) from \( \quiver{\reFo{R}} \) and a backward factor transition \( \parenPathWord{\vert{\blFo{h}}}{\blFo{\word{\inverted{\card{b}}}}}{\vert{\blFo{t}}} \) from \( \quiver{\blFo{S}} \), hence the product cardinal \( \cardinalProduct{\reFo{\card{r}},\blFo{\inverted{\card{b}}}} \).
The top middle entry is \( \tde{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{b}}}}{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{b}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{1}}}} \), which corresponds to a forward factor transition \( \parenPathWord{\vert{\reFo{t}}}{\reFo{\word{\card{r}}}}{\vert{\reFo{h}}} \), and an empty factor transition \( \parenPathWord{\vert{\blFo{b}}}{\emptyWord{}}{\vert{\blFo{b}}} \).
These constructors tell us how to manufacture product edges from the factor quivers. To understand the situation a bit better, we will now visualize the product quivers these constructors produce.
Visualizing graph products #
We can visualize the graph product in ways that help clarify the product structure. We'll use two methods to do this:
-
We will color vertices of the product by additive blending of the constituent vertices. For example, the product vertex \( \vertexProduct{\vert{\emToSy},\vert{\daTeFo{\fiToSy}}} \) will be displayed as \( \vert{\textcolor{b0d1d2}{\fiToSy}} \), and \( \vertexProduct{\vert{\reFo{\fiToSy}},\blFo{\vert{\fiToSy}}} \) as \( \vert{\orFo{\fiToSy}} \).
-
For graphs that can be laid out in one dimension, we will derive the \( \sym{y} \) coordinate of \( \vertexProduct{\vert{u},\vert{v}} \) from the one-dimensional coordinate of \( \vert{u} \) and the \( \sym{x} \) coordinate of \( \vertexProduct{\vert{u},\vert{v}} \) from the one-dimensional coordinate of \( \vert{v} \).
Let's examine the products we can form from \( \quiver{R} = \quiver{S} = \subSize{\lineQuiver }{2} \). These are the simplest factor quivers we can use that will yield a non-trivial result.
First we'll consider the product defined by \( \tde{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{t}}}}{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{h}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}}} \):
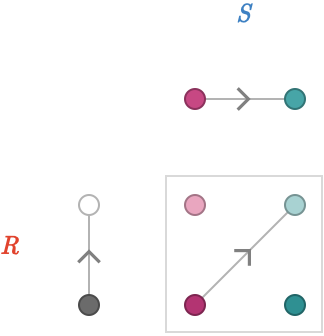
Since there is only one edge and therefore one 1-path in each factor quiver, there there is only one possible product edge. The orientation of this product edge matches the orientations of the factor edges.
Now consider the product defined by \( \tde{\vertexProduct{\vert{\reFo{t}},\vert{\blFo{b}}}}{\vertexProduct{\vert{\reFo{h}},\vert{\blFo{b}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{1}}}} \):
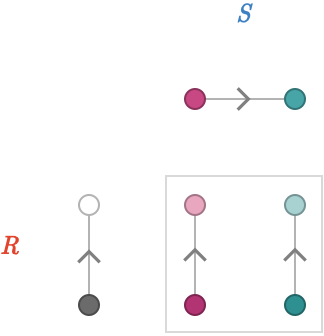
There are of course two 0-paths in \( \quiver{\blFo{S}} \), one for each vertex, and hence two possible product edges.
Lastly, consider the product defined by \( \tde{\vertexProduct{\vert{\reFo{r}},\vert{\blFo{b}}}}{\vertexProduct{\vert{\reFo{r}},\vert{\blFo{b}}}}{\cardinalProduct{\reFo{\card{1}},\blFo{\card{1}}}} \). This product does not depend on which edges are present in either quiver! It produces only self-loops:
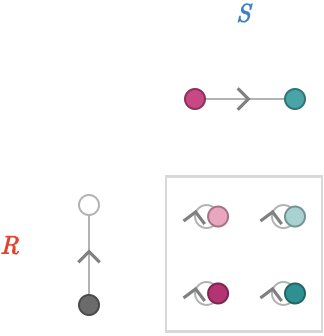
Let's revisit the original table of the 9 possible primitive product edge constructors:
\[ \begin{csarray}{ccc}{aii} \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{h}}}}{\reFo{\card{r}}}{\blFo{\card{b}}} & \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{b}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{b}}}}{\reFo{\card{r}}}{\blFo{\card{1}}} & \mtde{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{h}}}}{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{t}}}}{\reFo{\card{r}}}{\blFo{\inverted{\card{b}}}}\\[2em] \mtde{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{h}}}}{\reFo{\card{1}}}{\blFo{\card{b}}} & \mtde{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{b}}}}{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{b}}}}{\reFo{\card{1}}}{\blFo{\card{1}}} & \mtde{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{h}}}}{\verticalVertexProduct{\vert{\reFo{r}}}{\vert{\blFo{t}}}}{\reFo{\card{1}}}{\blFo{\inverted{\card{b}}}}\\[2em] \mtde{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{t}}}}{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{h}}}}{\reFo{\inverted{\card{r}}}}{\blFo{\card{b}}} & \mtde{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{b}}}}{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{b}}}}{\reFo{\inverted{\card{r}}}}{\blFo{\card{1}}} & \mtde{\verticalVertexProduct{\vert{\reFo{h}}}{\vert{\blFo{h}}}}{\verticalVertexProduct{\vert{\reFo{t}}}{\vert{\blFo{t}}}}{\reFo{\inverted{\card{r}}}}{\blFo{\inverted{\card{b}}}} \end{csarray} \]Notice that we can fully describe a product edge constructor by with the product cardinal labelling each product edge, since they fully determine the transitions corresponding to each product edge. Here we reproduce the above table using only these product cardinals:
\[ \begin{csarray}{ccc}{aii} \cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}} & \cardinalProduct{\reFo{\card{r}},\blFo{\card{1}}} & \cardinalProduct{\reFo{\card{r}},\blFo{\inverted{\card{b}}}}\\[2em] \cardinalProduct{\reFo{\card{1}},\blFo{\card{b}}} & \cardinalProduct{\reFo{\card{1}},\blFo{\card{1}}} & \cardinalProduct{\reFo{\card{1}},\blFo{\inverted{\card{b}}}}\\[2em] \cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\card{b}}} & \cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\card{1}}} & \cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\inverted{\card{b}}}} \end{csarray} \]Below we show the corresponding table of product quivers:

Arrow notation #
The disadvantage of using product cardinals like \( \cardinalProduct{\reFo{\card{r}},\blFo{\inverted{\card{b}}}} \) to describe product edge constructors is that we are relying on a redundant kind of notational convention: both the color (red) and the letter \( \reFo{\card{r}} \) is used to communicate the same idea -- that we are taking a forward transition in both of the factor quivers. We instead propose a simpler and more compact notation, called arrow notation, which uses only color.
Using arrow notation, a binary quiver product between \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) can be written as a kind of polynomial in the "variables" in two colors, being \( \reFo{\forwardFactor },\reFo{\backwardFactor },\reFo{\neutralFactor } \) and \( \blFo{\forwardFactor },\blFo{\backwardFactor },\blFo{\neutralFactor } \), which denote the different kinds of possible factor transitions from \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) respectively:
| z | z | z | z |
|---|---|---|---|
| \( \reFo{\forwardFactor } \) | forward \( \quiver{\reFo{R}} \)-transition: 1-path from \( \quiver{\reFo{R}} \) | \( \blFo{\forwardFactor } \) | forward \( \quiver{\blFo{S}} \)-transition: 1-path from \( \quiver{\blFo{S}} \) |
| \( \reFo{\backwardFactor } \) | backward \( \quiver{\reFo{R}} \)-transition: 1-path from \( \quiver{\reFo{R}} \) | \( \blFo{\backwardFactor } \) | backward \( \quiver{\blFo{S}} \)-transition: 1-path from \( \quiver{\blFo{S}} \) |
| \( \reFo{\neutralFactor } \) | neutral \( \quiver{\reFo{R}} \)-transition: 0-path from \( \quiver{\reFo{R}} \) | \( \blFo{\neutralFactor } \) | neutral \( \quiver{\blFo{S}} \)-transition: 0-path from \( \quiver{\blFo{S}} \) |
Each term of the polynomial is a degree-two monomial with one red variable and one blue variable, and represents a primitive product edge constructor.
Let's use this new notation to label the 9 primitive products of our two 2-line quivers, which are the 9 possible degree-2 monomials:
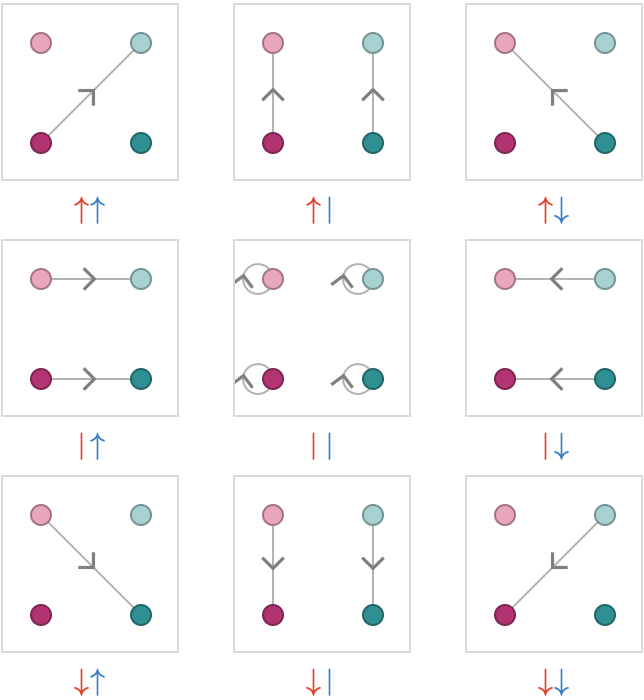
Sums of monomials #
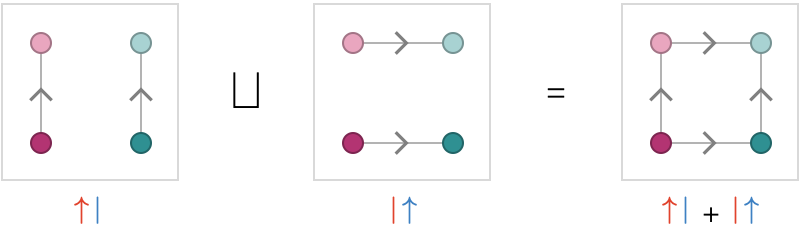
If we allow sums of these monomials, such as \( \quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\neutralFactor }+\reFo{\neutralFactor }\,\blFo{\forwardFactor }} \), we can express quiver products that contain the union of the corresponding primitive products:
Application notation #
If we wish to form a quiver product defined by a particular arrow polynomial, we would like to able to communicate which factor quivers are bound to which arrows. To do this, we will use a notation in which the factor quivers appear as the bottom row of a vertical expression, and the arrow appears as the top row. Color will then serve as the way in which we bind the factor quivers, written as symbols, with the arrows of the polynomial.
Here are several examples of products of two factor quivers named \( \quiver{R} \) and \( \quiver{S} \):
\[ \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \kern{20pt} \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\backwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \kern{20pt} \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\neutralFactor }+\reFo{\neutralFactor }\,\blFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \]The actual colors used do not matter -- they effectively act as local variables. The above products are identical to those shown below, which use two different colors that denote the same bindings between factor quivers and arrows:
\[ \frac{\quiverProdPoly{\piFo{\forwardFactor }\,\orFo{\forwardFactor }}} {\quiver{\piFo{R}},\quiver{\orFo{S}}} \kern{20pt} \frac{\quiverProdPoly{\piFo{\forwardFactor }\,\orFo{\backwardFactor }}} {\quiver{\piFo{R}},\quiver{\orFo{S}}} \kern{20pt} \frac{\quiverProdPoly{\piFo{\forwardFactor }\,\orFo{\neutralFactor }+\piFo{\neutralFactor }\,\orFo{\forwardFactor }}} {\quiver{\piFo{R}},\quiver{\orFo{S}}} \]We will also sometimes write an application in a compact form:
\[ {\quiverProdPoly{\piFo{\forwardFactor }\,\orFo{\forwardFactor }}} / {(\quiver{\piFo{R}},\quiver{\orFo{S}})} \kern{20pt} {\quiverProdPoly{\piFo{\forwardFactor }\,\orFo{\backwardFactor }}} / {(\quiver{\piFo{R}},\quiver{\orFo{S}})} \kern{20pt} {\paren{\quiverProdPoly{\piFo{\forwardFactor }\,\orFo{\neutralFactor }+\piFo{\neutralFactor }\,\orFo{\forwardFactor }}}} / {(\quiver{\piFo{R}},\quiver{\orFo{S}})} \]Symmetries under reversal #
At this point, it is useful to observe that the 9 constructors we enumerated are related to one another under edge reversal of the resulting products.
For example, the product defined by \( \quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }} \) is the edge reversal of the product defined by \( \quiverProdPoly{\reFo{\backwardFactor }\,\blFo{\backwardFactor }} \):
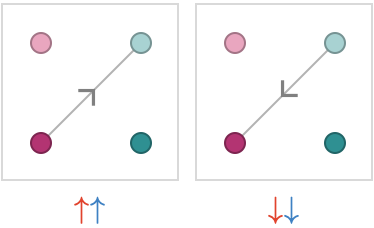
The explicit edges of these two products are given by \( \tde{\vert{\daPiFo{\fiToSy}}}{\vert{\liTeFo{\fiToSy}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}}} \) and \( \tde{\vert{\liTeFo{\fiToSy}}}{\vert{\daPiFo{\fiToSy}}}{\cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\inverted{\card{b}}}}} \). This suggests the structural property of product edges that the inversion of the product cardinal \( \cardinalProduct{\reFo{\card{r}},\blFo{\card{b}}} \) is the product cardinal \( \cardinalProduct{\reFo{\inverted{\card{r}}},\blFo{\inverted{\card{b}}}} \) -- in other words, that inversion distributes across the product.
Here we show the 9 constructors in columns, placed above their inverses:
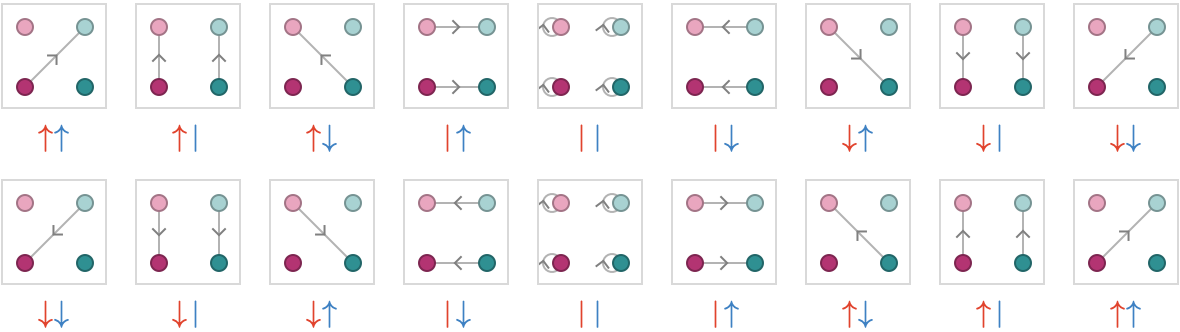
We can use notation to "pre-apply" inversion to the product polynomial rather than to the resulting product quiver. In other words, we can write the inversion of the product resulting from given quivers as the product of an inverted polynomial. The algebraic properties of this inversion operation on polynomials are:
\[ \begin{aligned} \inverted{\forwardFactor }&= \backwardFactor \\ \inverted{\neutralFactor }&= \neutralFactor \\ \inverted{\backwardFactor }&= \forwardFactor \\ \inverted{\quiverProdPoly{\sym{ \alpha }+\sym{ \beta }}}&= \quiverProdPoly{\inverted{\sym{ \alpha }}+\inverted{\sym{ \beta }}}\\ \inverted{\paren{\quiverProdPoly{\sym{ \alpha }\,\sym{ \beta }}}}&= \quiverProdPoly{\inverted{\sym{ \alpha }}\,\inverted{\sym{ \beta }}}\end{aligned} \]Here, \( \sym{ \alpha } \) and \( \sym{ \beta } \) represent arbitrary arrows, whether forward, backward, or neutral.
Distributivity #
We briefly examine the validity of the following distributivity law:
\[ \quiverProdPoly{\paren{\sym{ \alpha }+\sym{ \beta }}\,\sym{ \gamma }} = \quiverProdPoly{\quiverProdPoly{\sym{ \alpha }\,\sym{ \gamma }}+\quiverProdPoly{\sym{ \beta }\,\sym{ \gamma }}} \]As an example, taking \( \sym{ \alpha } = \reFo{\forwardFactor },\sym{ \beta } = \reFo{\backwardFactor },\sym{ \gamma } = \blFo{\forwardFactor } \), this manifests as the identity \( \quiverProdPoly{\paren{\reFo{\forwardFactor }+\reFo{\backwardFactor }}\,\blFo{\forwardFactor }} = \quiverProdPoly{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }}+\quiverProdPoly{\reFo{\backwardFactor }\,\blFo{\forwardFactor }}} \). What is the meaning of this identity? To unpack this, we will have to understand how we can evaluate this product in stages, first evaluating the part \( \quiverProdPoly{\reFo{\forwardFactor }+\reFo{\backwardFactor }} \) and then evaluating the product \( \quiverProdPoly{\plSqSy+\blFo{\forwardFactor }} \).
We can understand an arrow polynomial as a tree of evaluations -- the formal mathematical structure being known as an operad, which we will not elucidate here. For example, the product \( {\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }}} / {\paren{\quiver{\reFo{R}},\quiver{\blFo{S}}}} \) can be understood as the following tree, where the leaves of the tree are the quivers that are used as inputs to the arrow polynomial:
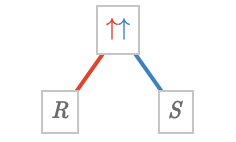
The factorization \( \quiverProdPoly{\paren{\reFo{\forwardFactor }+\reFo{\backwardFactor }}\,\blFo{\forwardFactor }} \) is depicted graphically below, in which we first evaluate a univariate product \( {\paren{\quiverProdPoly{\grFo{\forwardFactor }+\grFo{\backwardFactor }}}} / {\quiver{\grFo{R}}} \) and then use the result as the left factor for the product \( \quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }} \):
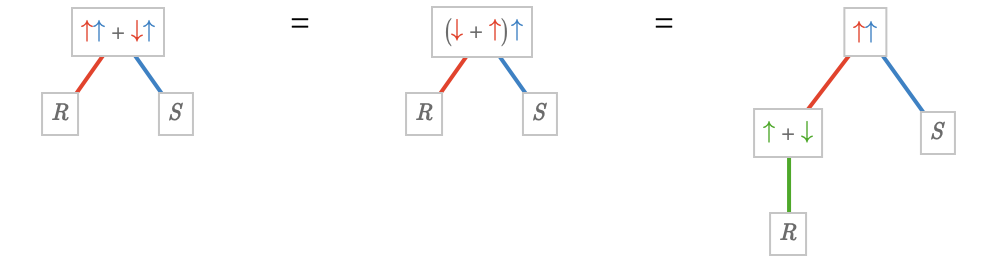
This corresponds to how we can factor the polynomial \( \sym{x} \, \sym{y} + \inverse{\sym{x}} \, \sym{y} \) into the product \( \paren{\sym{x} + \inverse{\sym{x}}} \, \sym{y} \), which can be evaluated on particular inputs in a staged fashion
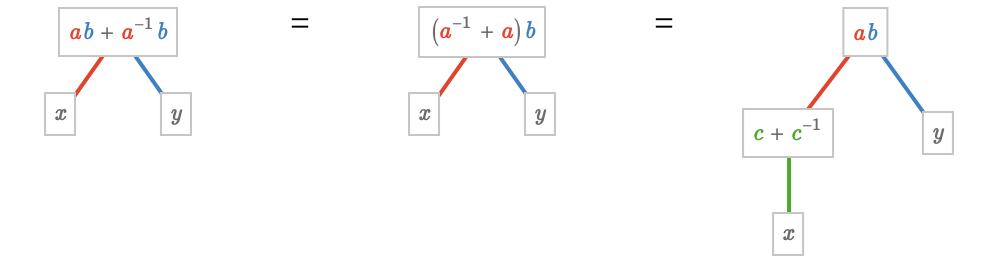
Again, notice that the colors and symbols \( \sym{a},\sym{b},\sym{c} \) serve a purely notational role, depicting how to bind the inputs of each polynomial evaluation. We can replace these symbols and colors with any others we like to describe the exact same product.
Unary products #
It is interesting to examine the three products we can form from a single quiver using the monomials \( \forwardFactor ,\neutralFactor ,\backwardFactor \). They are shown below for a finite line quiver in the first row and a finite square quiver in the second row:

In short, the forward constructor \( \forwardFactor \) acts like the identity, the backward constructor \( \backwardFactor \) reverses all edges, and the neutral constructor \( \neutralFactor \) has the effect of disconnecting the quiver, creating self-loops for each vertex. Let's make this explicit for the line quiver:
\[ \begin{aligned} {\quiverProdPoly{\quiver{\forwardFactor }}} / {\bindCardSize{\subSize{\lineQuiver }{4}}{\reFo{\card{r}}}}&= \bindCardSize{\subSize{\lineQuiver }{4}}{\cardinalProduct{\reFo{\card{r}}}}\\[1em] {\quiverProdPoly{\quiver{\backwardFactor }}} / {\bindCardSize{\subSize{\lineQuiver }{4}}{\reFo{\card{r}}}}&= \bindCardSize{\subSize{\lineQuiver }{4}}{\cardinalProduct{\reFo{\inverted{\card{r}}}}}\\[1em] {\quiverProdPoly{\quiver{\neutralFactor }}} / {\bindCardSize{\subSize{\lineQuiver }{4}}{\reFo{\card{r}}}}&= \indexGraphDisjointUnion{\bindCardSize{\subSize{\cycleQuiver }{1}}{\cardinalProduct{\reFo{\card{1}}}}}{4}{}\end{aligned} \]We can write this behavior for a general quiver as:
\[ \begin{aligned} {\quiverProdPoly{\quiver{\forwardFactor }}} / {\quiver{Q}}&\homeomorphicSymbol\quiver{Q}\\[1em] {\quiverProdPoly{\quiver{\backwardFactor }}} / {\quiver{Q}}&\homeomorphicSymbol\inverted{\quiver{Q}}\\[1em] {\quiverProdPoly{\quiver{\neutralFactor }}} / {\quiver{Q}}&\homeomorphicSymbol\indexGraphDisjointUnion{\subSize{\cycleQuiver }{1}}{\vertexCountOf{\quiver{Q}}}{}\end{aligned} \]Named binary products #
Equipped with our new, compact notation for building products out of sums of primitive edge constructors, we will now enumerate and name some of the possible binary products.
Locked product #
We'll introduce a binary quiver product called the locked quiver product, denoted \( \lockedQuiverProductSymbol \). This product is related to the notion of the tensor graph product \( \otimes \) of undirected graphs.
The locked quiver product \( \quiver{R}\lockedQuiverProductSymbol \quiver{S} \) of two quivers \( \quiver{R},\quiver{S} \) is defined to be:
\[ \quiver{R}\lockedQuiverProductSymbol \quiver{S}\defEqualSymbol \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \]We use the word locked to indicate that the transitions of the two factor quivers are locked together in the same, forward orientation.
Let's examine \( \quiver{R}\lockedQuiverProductSymbol \quiver{S} \), where \( \quiver{R} = \quiver{S} = \subSize{\lineQuiver }{2} \):
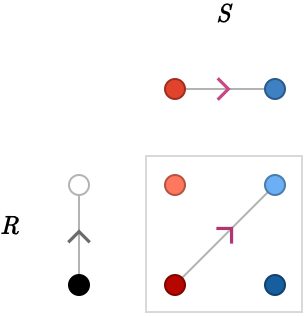
Let's enlarge \( \quiver{S} \), setting \( \quiver{S} = \subSize{\lineQuiver }{3} \):
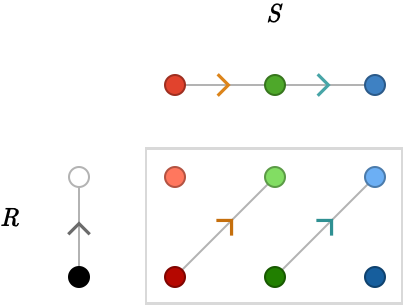
Finally let's enlarge \( \quiver{R} \), setting \( \quiver{R} = \subSize{\lineQuiver }{3} \):
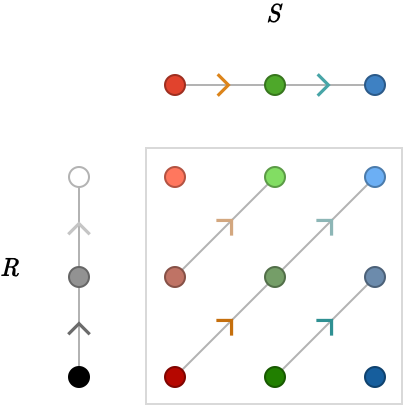
Free products #
We now introduce the right-free quiver product \( \quiver{R}\rightFreeQuiverProductSymbol \quiver{S} \), which involves always taking the forward transition for the left factor and taking either the forward, neutral, or backward transition for the right factor. Explicitly:
\[ \quiver{R}\rightFreeQuiverProductSymbol \quiver{S}\defEqualSymbol \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }+\reFo{\forwardFactor }\,\blFo{\neutralFactor }+\reFo{\forwardFactor }\,\blFo{\backwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} = \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\paren{\blFo{\forwardFactor }+\blFo{\neutralFactor }+\blFo{\backwardFactor }}}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} = \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardBackwardNeutralFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \]Here we are using the notation \( \forwardBackwardNeutralFactor \syntaxEqualSymbol \paren{\quiverProdPoly{\quiver{\forwardFactor }+\quiver{\neutralFactor }+\quiver{\backwardFactor }}} \).
The left-free quiver product is defined how you would expect:
\[ \quiver{R}\leftFreeQuiverProductSymbol \quiver{S}\defEqualSymbol \frac{\quiverProdPoly{\reFo{\forwardBackwardNeutralFactor }\,\blFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \]Cartesian product #
The Cartesian product \( \quiver{R}\cartesianQuiverProductSymbol \quiver{S} \) is defined by taking only one factor transition, taken from either factor, combined with the neutral factor from the other factor. Explicitly:
\[ \quiver{R}\cartesianQuiverProductSymbol \quiver{S}\defEqualSymbol \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\neutralFactor }+\reFo{\neutralFactor }\,\blFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\blFo{S}}} \]Visualization #
Let's visualize the free quiver products and contrast them with the locked and Cartesian quiver product. Let's start with the same products we considered earlier:
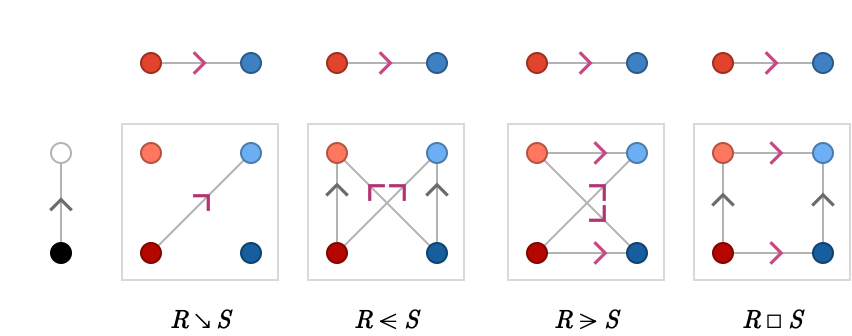
Notice that for the free products and the Cartesian product we no longer have vertices that are totally disconnected.
Let's enlarge \( \quiver{S} \), setting \( \quiver{S} = \subSize{\lineQuiver }{3} \):
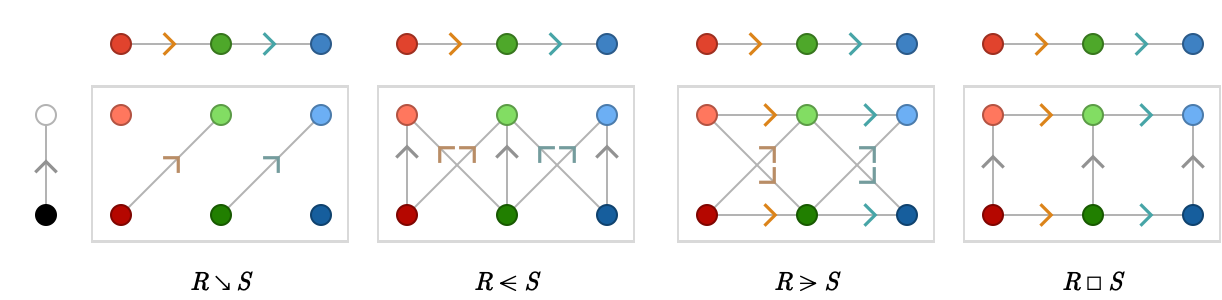
Now let's enlarge \( \quiver{R} \), setting \( \quiver{R} = \subSize{\lineQuiver }{3} \):
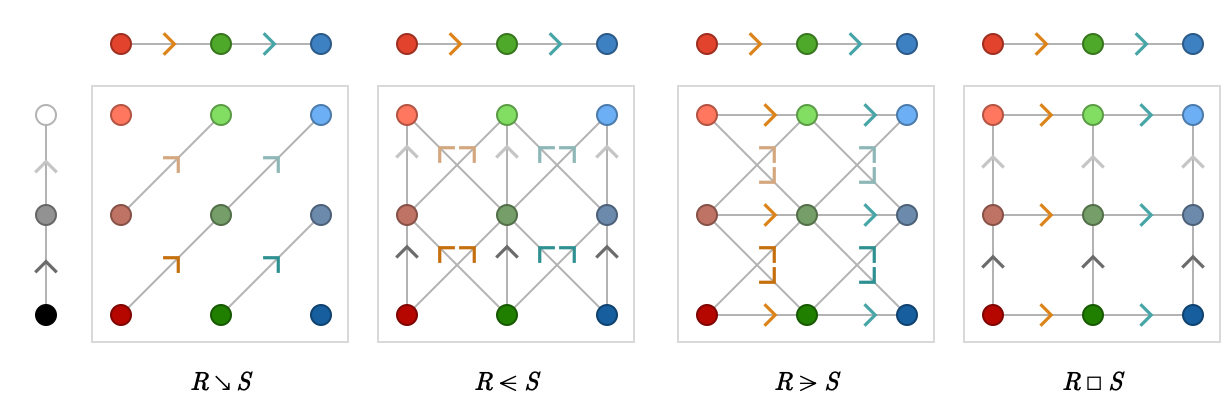
Summary #
The following table lists the named products we have defined above:
| z | z | z |
|---|---|---|
| locked | \( \quiver{\reFo{R}}\dependentQuiverProductSymbol \quiver{\blFo{S}} \) | \( \quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardFactor }} \) |
| left free | \( \quiver{\reFo{R}}\leftFreeQuiverProductSymbol \quiver{\blFo{S}} \) | \( \quiverProdPoly{\reFo{\forwardBackwardNeutralFactor }\,\blFo{\forwardFactor }} \) |
| right free | \( \quiver{\reFo{R}}\rightFreeQuiverProductSymbol \quiver{\blFo{S}} \) | \( \quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\forwardBackwardNeutralFactor }} \) |
| Cartesian | \( \quiver{\reFo{R}}\cartesianQuiverProductSymbol \quiver{\blFo{S}} \) | \( \quiverProdPoly{\reFo{\forwardFactor }\,\blFo{\neutralFactor }+\reFo{\neutralFactor }\,\blFo{\forwardFactor }} \) |
Transitive quivers #
Square quiver #
The first application of the products we have defined above will be to construct the square quiver as a product of two line quivers.
Let's start with the Cartesian product \( \subSize{\lineQuiver }{ \infty }\cartesianQuiverProductSymbol \subSize{\lineQuiver }{ \infty } \) between two infinite line lattices \( \subSize{\lineQuiver }{ \infty } \):

We obtain the infinite square quiver: \( \subSize{\lineQuiver }{ \infty }\cartesianQuiverProductSymbol \subSize{\lineQuiver }{ \infty }\isomorphicSymbol \subSize{\squareQuiver }{ \infty } \)
Let's limit ourselves to the Cartesian product of two finite line quivers, \( \subSize{\lineQuiver }{3}\cartesianQuiverProductSymbol \subSize{\lineQuiver }{2} \):
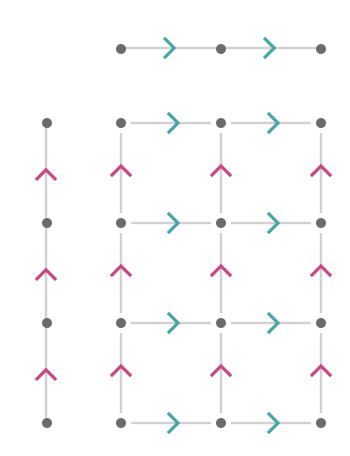
We obtain the finite rectangular quiver \( \bindCardSize{\squareQuiver }{3,2} \). We can generalize to arbitrary sizes easily, and include the cardinal bindings:
\[ \bindCardSize{\lineQuiver }{\orFo{\card{x}}\compactBindingRuleSymbol \sym{w}}\cartesianQuiverProductSymbol \bindCardSize{\lineQuiver }{\piFo{\card{y}}\compactBindingRuleSymbol \sym{h}}\isomorphicSymbol \bindCardSize{\squareQuiver }{\orFo{\card{x}}\compactBindingRuleSymbol \sym{w},\piFo{\card{y}}\compactBindingRuleSymbol \sym{h}} \]Setting \( \sym{n} = \infty \) we obtain the special case \( \bindCardSize{\subSize{\lineQuiver }{ \infty }}{\orFo{\card{x}}}\cartesianQuiverProductSymbol \bindCardSize{\subSize{\lineQuiver }{ \infty }}{\piFo{\card{y}}}\isomorphicSymbol \bindCardSize{\subSize{\squareQuiver }{ \infty }}{\orFo{\card{x}},\piFo{\card{y}}} \).
Triangular quiver #
We need not limit ourselves to products between two quivers.
Let us define the triangular product \( \function{ \Delta }(\quiver{R},\quiver{G},\quiver{B}) \) between three quivers as follows:
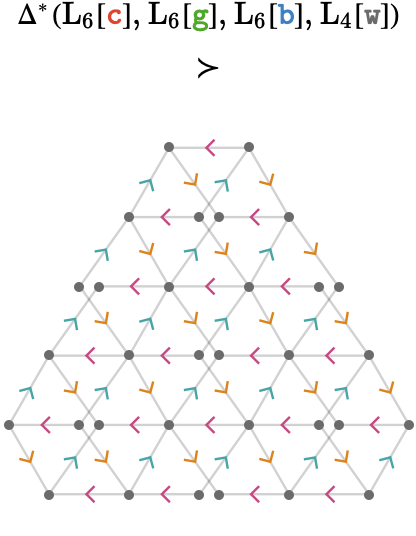
\[ \function{ \Delta }(\quiver{R},\quiver{G},\quiver{B})\defEqualSymbol \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\grFo{\backwardFactor }\,\blFo{\neutralFactor }+\reFo{\neutralFactor }\,\grFo{\forwardFactor }\,\blFo{\backwardFactor }+\reFo{\backwardFactor }\,\grFo{\neutralFactor }\,\blFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\grFo{G}},\quiver{\blFo{B}}} \]Here we show the largest connected component of the the triangular product between three finite line lattices of size 5:
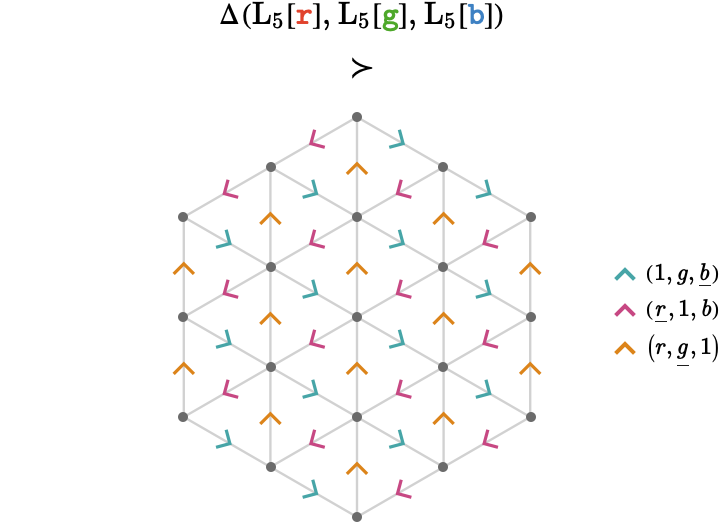
We have colored the product cardinals by the additive blend of the graphs involved, so that \( \quiverProdPoly{\reFo{\forwardFactor }\,\grFo{\backwardFactor }} \) is represented by the arrowhead \( \teFo{\arSy} \), \( \poly{\grFo{\forwardFactor } \, \blFo{\backwardFactor }} \) by \( \orFo{\arSy} \), and \( \quiverProdPoly{\blFo{\forwardFactor }\,\reFo{\backwardFactor }} \) by \( \piFo{\arSy} \). The symbol \( \componentSuperQuiverOfSymbol \) means "contains the connected component".
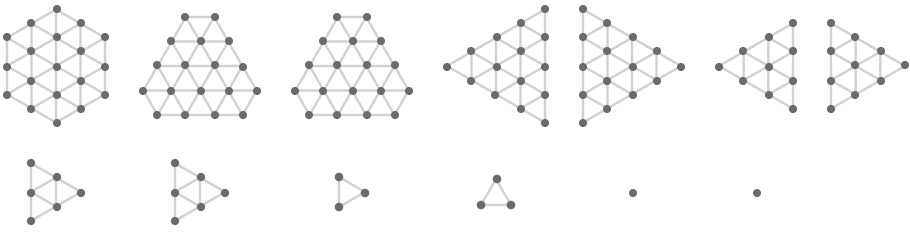
The full set of connected components correspond to slices through a larger object which we will describe in the next section.
Infinite product #
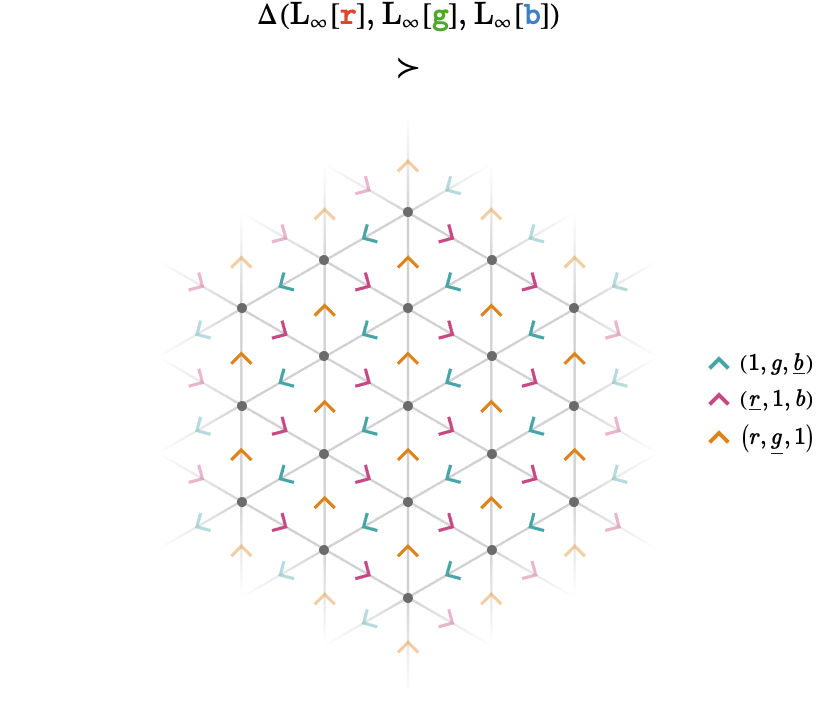
The product between three infinite line lattices, \( \function{ \Delta }(\subSize{\lineQuiver }{ \infty },\subSize{\lineQuiver }{ \infty },\subSize{\lineQuiver }{ \infty }) \), contains countably infinite connected components, each of which is isomorphic to the infinite line quiver:
\[ \function{ \Delta }(\bindCardSize{\subSize{\lineQuiver }{ \infty }}{\reFo{\card{r}}},\bindCardSize{\subSize{\lineQuiver }{ \infty }}{\grFo{\card{g}}},\bindCardSize{\subSize{\lineQuiver }{ \infty }}{\blFo{\card{b}}})\homeomorphicSymbol \indexGraphDisjointUnion{\subSize{\triangularQuiver }{ \infty }}{\mathbb{Z}}{} \]We depict this visually below:
Projections #
Quiver products are explicitly constructed out of combinations of transitions of their factor quivers. This means that we have a straightforward way to project from a path in the product quiver to any of its factor quivers, by simply composing the transitions for that particular factor along the given path.
Let's examine an example of the square quiver \( \bindCardSize{\subSize{\squareQuiver }{3}}{\reFo{\card{x}},\blFo{\card{y}}} \), isomorphic to the product \( \bindCardSize{\subSize{\lineQuiver }{3}}{\reFo{\card{r}}}\cartesianQuiverProductSymbol \bindCardSize{\subSize{\lineQuiver }{3}}{\blFo{\card{b}}} \) by identifying the cardinals \( \reFo{\card{x}}\isomorphicSymbol \cardinalProduct{\reFo{\card{r}},\blFo{1}},\blFo{\card{y}}\isomorphicSymbol \cardinalProduct{\reFo{1},\blFo{\card{b}}} \).
Below we show a path \( \path{P_{\quiver{\piFo{Q}}}} = \pathWord{\vertexProduct{2,2}}{\word{\blFo{\card{y}}}{\reFo{\card{x}}}{\blFo{\ncard{y}}}{\blFo{\ncard{y}}}{\reFo{\card{x}}}}{\vertexProduct{4,1}} \) in the product quiver \( \quiver{\piFo{Q}} = \quiver{\reFo{R}}\cartesianQuiverProductSymbol \quiver{\blFo{S}} \), and the corresponding projected paths \( \path{P_{\quiver{\reFo{R}}}},\path{P_{\quiver{\blFo{S}}}} \) in the two factors \( \quiver{\reFo{R}},\quiver{\blFo{S}} \):
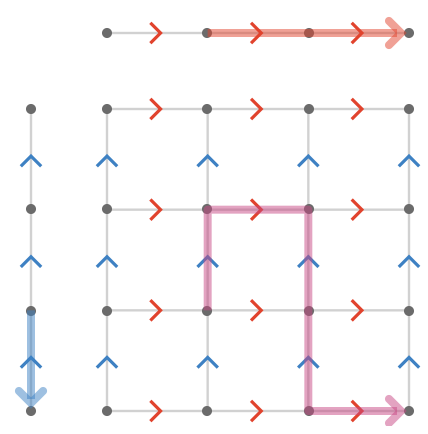
The two factor paths are obtained by writing the path \( \path{P_{\quiver{\piFo{Q}}}} \) in terms of product cardinals \( \cardinalProduct{\reFo{\card{r}},\blFo{\card{1}}},\cardinalProduct{\reFo{\card{1}},\blFo{\card{b}}} \) rather than the aliases \( \reFo{\card{x}},\blFo{\card{y}} \). Then we have:
\[ \path{P_{\quiver{\piFo{Q}}}} = \pathWord{\vertexProduct{1,2}}{\word{\cardinalProduct{\reFo{\card{1}},\blFo{\card{b}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{1}}}}{\cardinalProduct{\reFo{\card{1}},\blFo{\inverted{\card{b}}}}}{\cardinalProduct{\reFo{\card{1}},\blFo{\inverted{\card{b}}}}}{\cardinalProduct{\reFo{\card{r}},\blFo{\card{1}}}}}{\vertexProduct{4,1}} \]Writing this path vertically, we can more easily see how the projections are formed:
\[ \path{P_{\quiver{\piFo{Q}}}} = \pathWord{\verticalVertexProduct{2}{2}}{\word{\verticalCardinalProduct{\reFo{\card{1}}}{\blFo{\card{b}}}}{\verticalCardinalProduct{\reFo{\card{r}}}{\blFo{\card{1}}}}{\verticalCardinalProduct{\reFo{\card{1}}}{\blFo{\inverted{\card{b}}}}}{\verticalCardinalProduct{\reFo{\card{1}}}{\blFo{\inverted{\card{b}}}}}{\verticalCardinalProduct{\reFo{\card{r}}}{\blFo{\card{1}}}}}{\verticalVertexProduct{4}{1}} \]The projections are the top half and bottom half of this path:
\[ \begin{aligned} \path{P_{\quiver{\reFo{R}}}}&= \pathWord{2}{\word{\reFo{\card{1}}}{\reFo{\card{r}}}{\reFo{\card{1}}}{\reFo{\card{1}}}{\reFo{\card{r}}}}{4}&= \pathWord{2}{\word{\reFo{\card{r}}}{\reFo{\card{r}}}}{4}\\ \path{P_{\quiver{\blFo{S}}}}&= \pathWord{2}{\word{\blFo{\card{b}}}{\blFo{\card{1}}}{\blFo{\ncard{b}}}{\blFo{\ncard{b}}}{\blFo{\card{1}}}}{1}&= \pathWord{2}{\word{\blFo{\card{b}}}{\blFo{\inverted{\card{b}}}}{\blFo{\inverted{\card{b}}}}}{1}&= \pathWord{2}{\word{\blFo{\inverted{\card{b}}}}}{1}\end{aligned} \]Notice that we were able to apply word reduction to the factor path words once they had been obtained, which made them shorter than the original product path word.
There are two path homomorphisms, written \( \functionSignature{\pathHomomorphism{ \pi _{\quiver{\reFo{R}}}}}{\pathGroupoid{\quiver{\piFo{Q}}}}{\pathGroupoid{\quiver{\reFo{R}}}} \) and \( \functionSignature{\pathHomomorphism{ \pi _{\quiver{\blFo{S}}}}}{\pathGroupoid{\quiver{\piFo{Q}}}}{\pathGroupoid{\quiver{\blFo{S}}}} \), that project any path in \( \quiver{\piFo{Q}} \) to its factor path in \( \quiver{\reFo{R}} \) and \( \quiver{\blFo{S}} \) respectively. Then our examples of course illustrate \( \pathHomomorphism{ \pi _{\quiver{\reFo{R}}}}(\path{P_{\quiver{\piFo{Q}}}}) = \path{P_{\quiver{\reFo{R}}}} \) and \( \pathHomomorphism{ \pi _{\quiver{\blFo{S}}}}(\path{P_{\quiver{\piFo{Q}}}}) = \path{P_{\quiver{\blFo{S}}}} \).
This of course generalizes to higher-arity products. For a product with \( \sym{n} \) factors, we can label these projection homomorphisms \( \pathHomomorphism{ \pi _1},\pathHomomorphism{ \pi _2},\elSy,\pathHomomorphism{ \pi _{\sym{n}}} \).
Coverings? #
The projections \( \pathHomomorphism{ \pi _1},\pathHomomorphism{ \pi _2},\elSy,\pathHomomorphism{ \pi _{\sym{n}}} \) associated with an \( \sym{n} \)-ary product \( \quiver{Q} = {\quiverProdPoly{\sym{ \gamma }}} / {\paren{\quiver{R_1},\elSy,\quiver{R_{\sym{n}}}}} \) are by definition surjective path homomorphisms. However, they are not in general length-preserving, as we saw in the above example. This implies that \( \quiver{Q} \) is not in general a cover of the quivers \( \quiver{R_{\sym{i}}} \), as one might first expect.
Intransitive lattices #
Hexagonal quiver #
It might seem that we cannot construct intransitive quivers, such as the hexagonal lattice, as products of transitive quivers. And this is true. But finite line lattices are not transitive: their two end vertices are different from the others. Surprisingly, we can construct the hexagonal lattice by including one additional factor quiver, being the 2-line lattice. Here is the product that accomplishes this, which we will call the hexagonal product:
\[ \function{\starModifier{ \Delta }}(\quiver{R},\quiver{G},\quiver{B},\quiver{X})\defEqualSymbol \function{ \Delta }(\quiver{R},\quiver{G},\quiver{B})\lockedQuiverProductSymbol \quiver{X} = \frac{\quiverProdPoly{\reFo{\forwardFactor }\,\grFo{\backwardFactor }\,\blFo{\neutralFactor }\,\daGFo{\forwardFactor }+\reFo{\neutralFactor }\,\grFo{\forwardFactor }\,\blFo{\backwardFactor }\,\daGFo{\forwardFactor }+\reFo{\backwardFactor }\,\grFo{\neutralFactor }\,\blFo{\forwardFactor }\,\daGFo{\forwardFactor }}} {\quiver{\reFo{R}},\quiver{\grFo{G}},\quiver{\blFo{B}},\gFo{\quiver{X}}} \]Let's examine an example, taking \( \reFo{\quiver{R}},\grFo{\quiver{G}},\blFo{\quiver{B}} \) to be copies of \( \subSize{\lineQuiver }{\sym{n}} \) as before, with \( \gFo{\quiver{X}} \) being \( \subSize{\lineQuiver }{2} \). For \( \sym{n} = 8 \) we obtain:
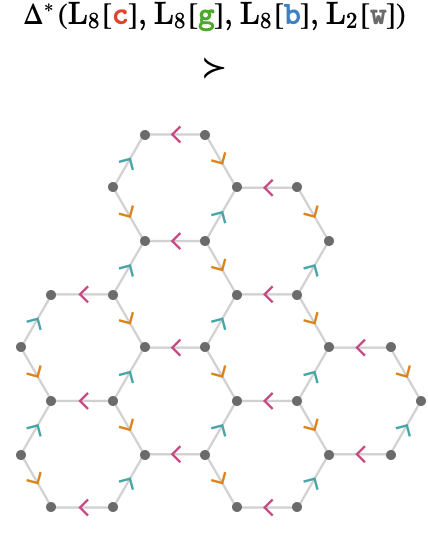
Here is the full set of connected graph components, this time for \( \sym{n} = 6 \).

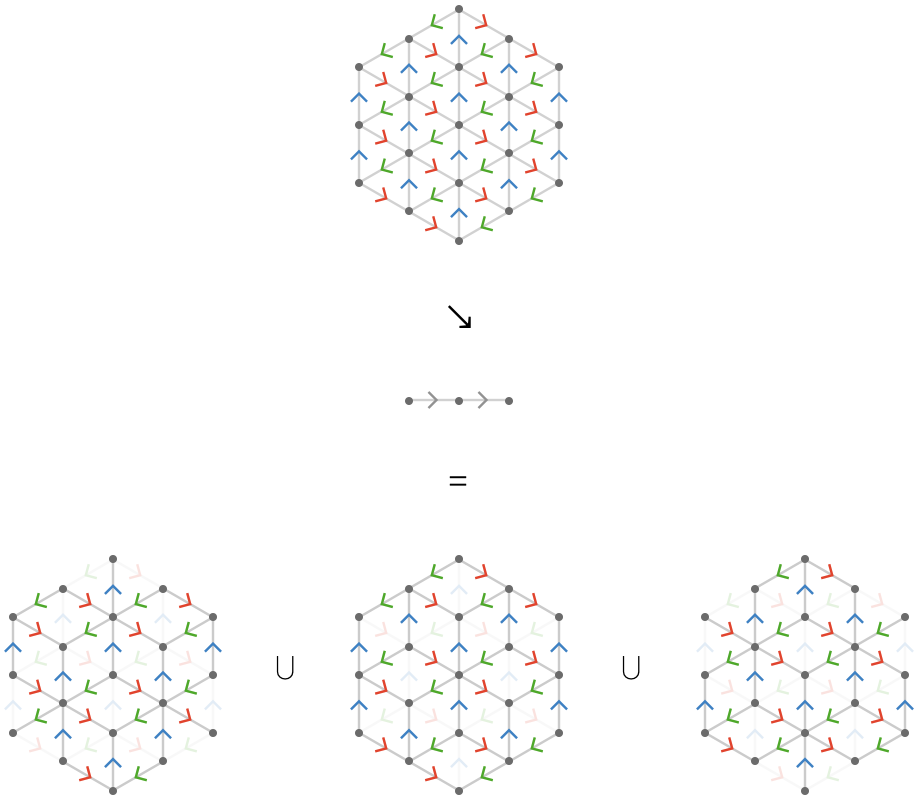
We can also interpret the factorization \( \quiverProdPoly{\reFo{\forwardFactor }\,\grFo{\backwardFactor }\,\blFo{\neutralFactor }\,\daGFo{\forwardFactor }+\reFo{\neutralFactor }\,\grFo{\forwardFactor }\,\blFo{\backwardFactor }\,\daGFo{\forwardFactor }+\reFo{\backwardFactor }\,\grFo{\neutralFactor }\,\blFo{\forwardFactor }\,\daGFo{\forwardFactor }} = \quiverProdPoly{\paren{\reFo{\forwardFactor }\,\grFo{\backwardFactor }\,\blFo{\neutralFactor }+\reFo{\neutralFactor }\,\grFo{\forwardFactor }\,\blFo{\backwardFactor }+\reFo{\backwardFactor }\,\grFo{\neutralFactor }\,\blFo{\forwardFactor }}\,\daGFo{\forwardFactor }} \) as stating that we can obtain the hexagonal lattice quiver as the locked product of the triangular lattice quiver with the 2-line quiver. In fact, three copies of the triangular lattice are produced, shown below:
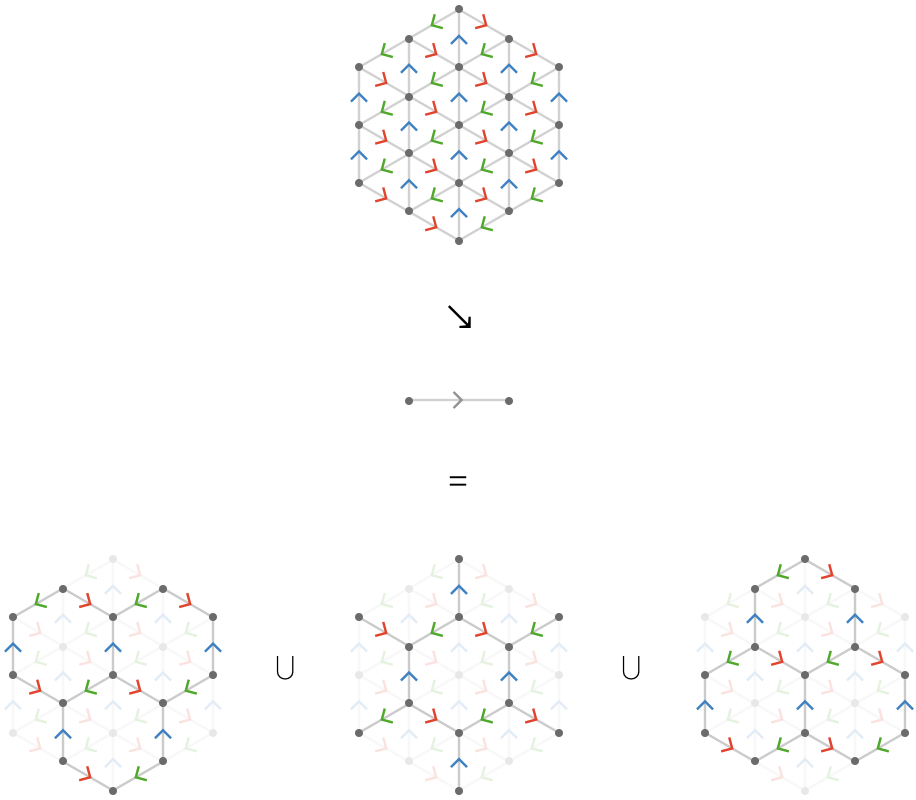
An important fact is that the number of connected components (three) does not depend on the size of the \( \reFo{\quiver{R}},\grFo{\quiver{G}},\blFo{\quiver{B}} \) line lattices, which leads to the theorem:
\[ \bindCardSize{\subSize{\triangularQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}\lockedQuiverProductSymbol \bindCardSize{\subSize{\lineQuiver }{2}}{\daGFo{\card{x}}}\homeomorphicSymbol \indexGraphDisjointUnion{\bindCardSize{\subSize{\hexagonalQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}}{\sym{i}}{3} \]Since the triangular product produces countably infinite copies of the triangular lattice, we also have this property of the hexagonal product:
\[ \function{\starModifier{ \Delta }}(\bindCardSize{\subSize{\lineQuiver }{ \infty }}{\reFo{\card{c}}},\bindCardSize{\subSize{\lineQuiver }{ \infty }}{\grFo{\card{g}}},\bindCardSize{\subSize{\lineQuiver }{ \infty }}{\blFo{\card{b}}},\bindCardSize{\subSize{\lineQuiver }{2}}{\daGFo{\card{w}}})\homeomorphicSymbol \indexGraphDisjointUnion{\bindCardSize{\subSize{\hexagonalQuiver }{ \infty }}{\reFo{\card{r}},\grFo{\card{g}},\blFo{\card{b}}}}{\sym{i}}{ \infty } \]Rhombille quiver #
Extending \( \gFo{\quiver{X}} \) to be a 3-line lattice yields the rhombille lattice:
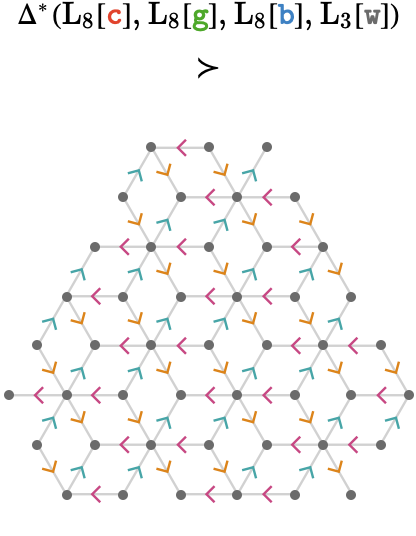
Again, the factorization gives us an alternative way of building the rhombille lattice, again showing the three connected components:
Extending \( \gFo{\quiver{X}} \) to be a 4-line lattice yields the "alternating rhombille lattice", which involves a similar motif to the rhombille lattice, in which vertices alternate between degree 3 and degree 6:
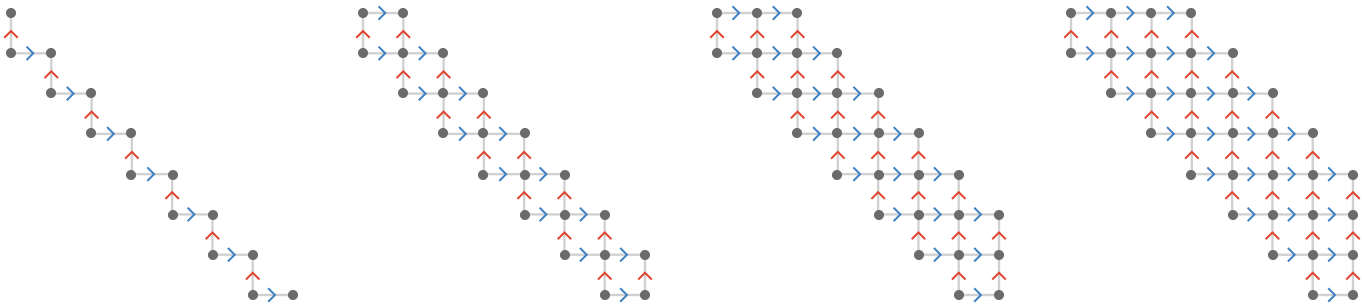
Returning to the square lattice, we apply the same technique to obtain non-transitive versions of the square lattice. Here, we compute:
\[ \quiverProdPoly{\reFo{\forwardFactor }\,\daGFo{\forwardFactor }+\blFo{\forwardFactor }\,\daGFo{\forwardFactor }} \]while varying \( \gFo{\quiver{X}} \) between a 2-line lattice and a 5-line lattice:
Decomposition of products #
In the previous section we decomposed the non-transitive hexagonal and rhombille lattices into their connected components. We now extend this technique to the earlier products we examined, so we can better understand how they produce fragments of corresponding lattice quivers.
As before, we'll visualize these as by superimposing each connected component on top of the full union of all connected components, shown dimmed. Note that it may appear that the union itself is fully connected, but when this occurs it is an artefact of the projection onto two dimensions.
Square decomposition #
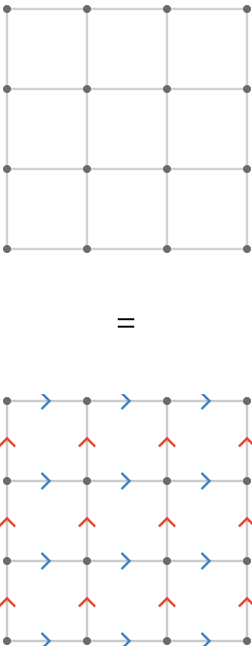
The Cartesian product \( \quiverProdPoly{\reFo{\forwardFactor }+\blFo{\forwardFactor }} \) decomposition is trivial, since the Cartesian product of two line lattices yields a single connected graph.
Triangular decomposition #
The triangular product \( \quiverProdPoly{\reFo{\forwardFactor }\,\grFo{\backwardFactor }+\grFo{\forwardFactor }\,\blFo{\backwardFactor }+\blFo{\forwardFactor }\,\reFo{\backwardFactor }} \) is more interesting, yielding a "stack" of disconnected components:
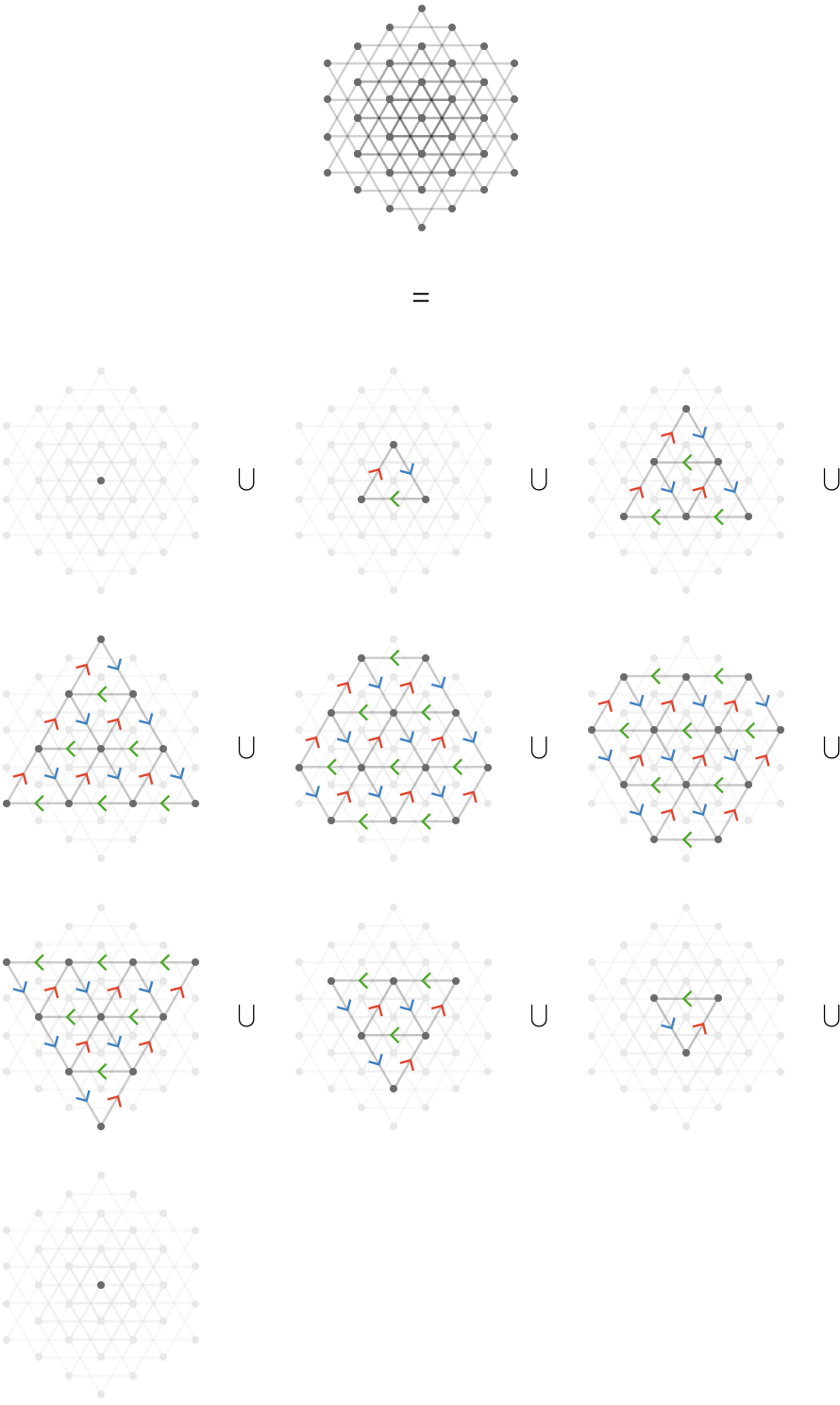
These components correspond to angled slices through the vertices of a cubic grid. Here we show a smaller fragment to avoid clutter, from an angle to emphasize the separate planes that yield the connected components:
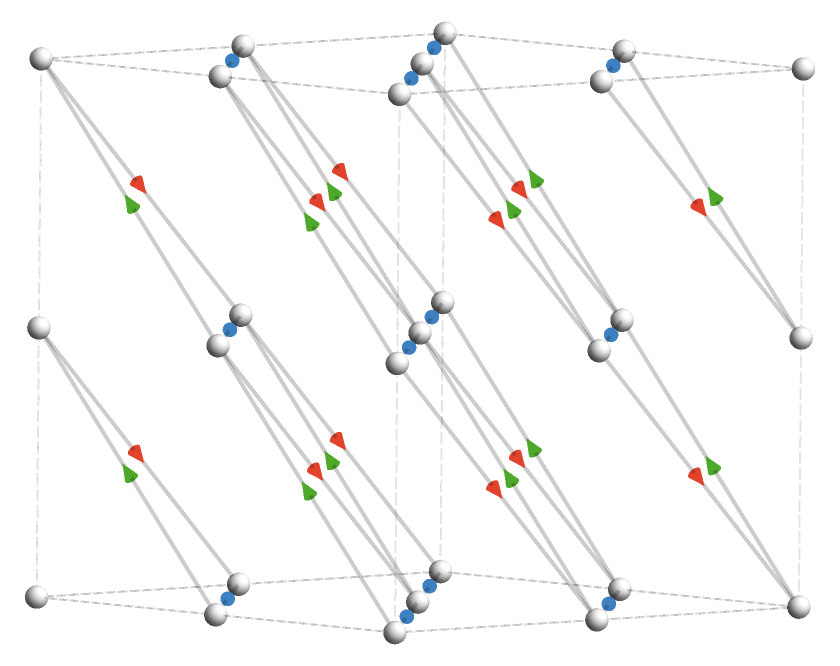
And from another angle to emphasize the hexagonal structure of each plane:
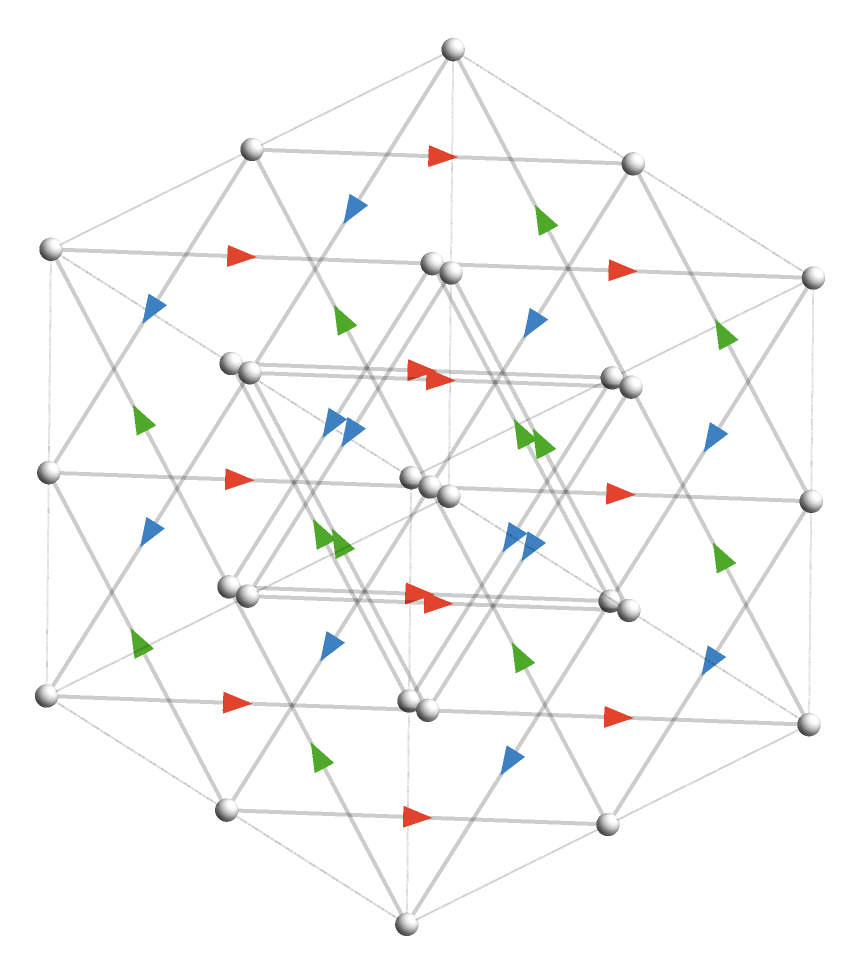
Hexagonal decomposition #
The hexagonal product \( \quiverProdPoly{\reFo{\forwardFactor }\,\grFo{\backwardFactor }\,\daGFo{\forwardFactor }+\grFo{\forwardFactor }\,\blFo{\backwardFactor }\,\daGFo{\forwardFactor }+\blFo{\forwardFactor }\,\reFo{\backwardFactor }\,\daGFo{\forwardFactor }} \) is similar to the triangular product, except with more slices possible:

The corresponding higher-dimensional object of which the connected components are slices is 4-dimensional, and cannot easily be visualized. Notice that the appearance of two single vertex connected components above is a reflection of the fact that there are two product vertices (corresponding to the two \( \gFo{\quiver{X}} \)-vertices) whose whose projections into 2 (and 3) dimensions coincide.
Square products #
Finally, we can decompose the product of the square lattice with a 2-line lattice:
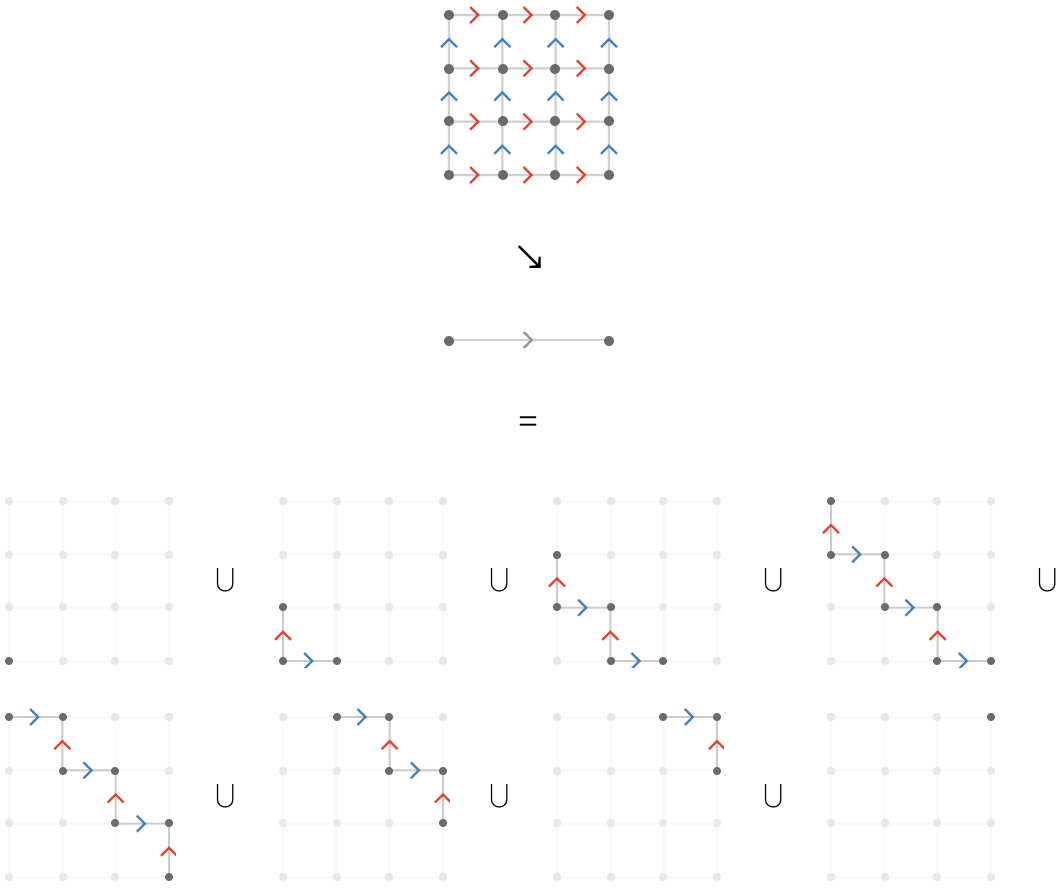
Unlike the case with the product of the triangular lattice with the 2-line, we have a large number of connected components that depends on the size of the finite square lattice. We can see these components as slices of the following three-dimensional slab in which the \( \gFo{\quiver{X}} \)-axis has length 2, depicted going into the page:
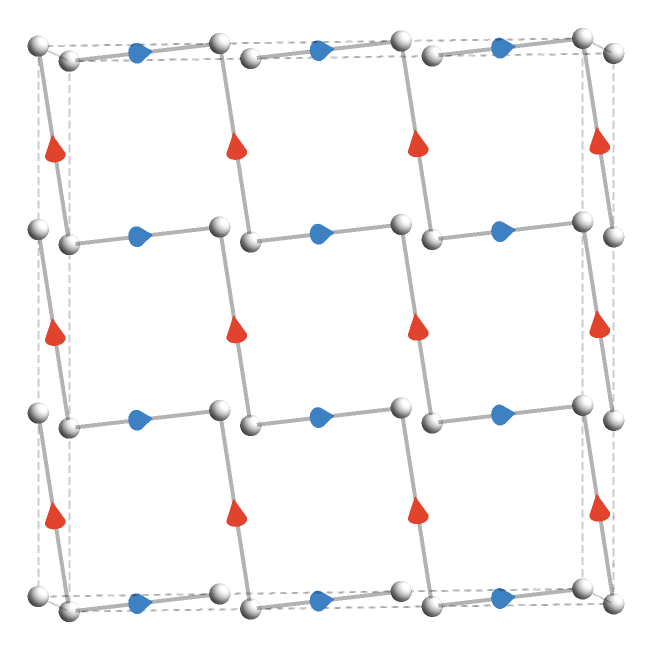
Here the \( \gFo{\quiver{X}} \)-axis is depicted vertically, and the connected components are more easily seen:
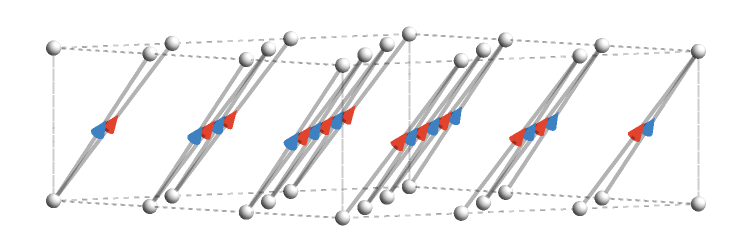
For a 3-line lattice we obtain a "thicker stripe" that scans across the square:
This corresponds to slices of a three-dimensional slab where the \( \gFo{\quiver{X}} \)-axis has length 3, depicted going into the page.
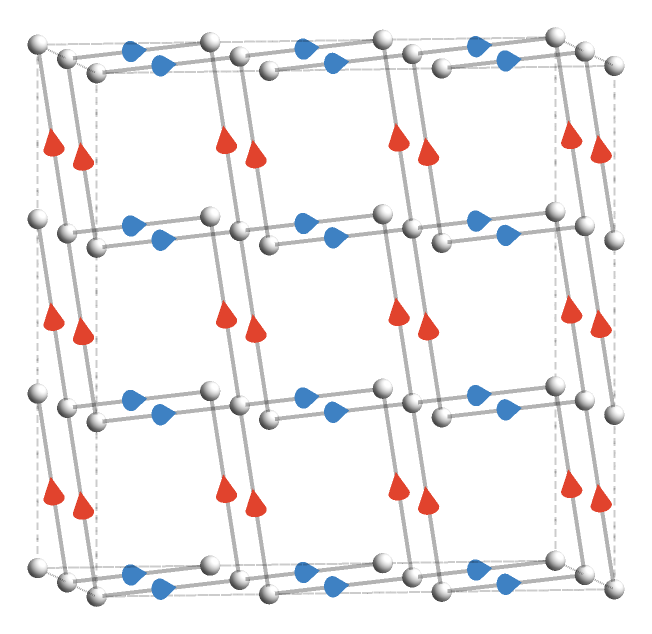
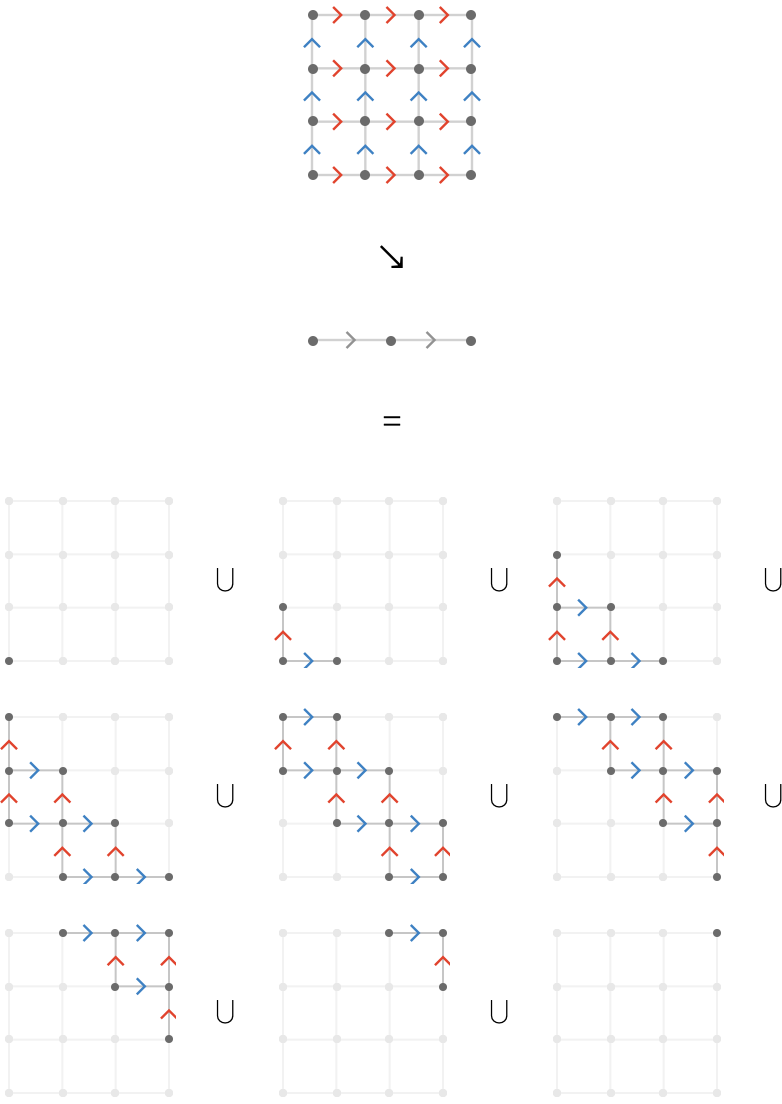
Here the \( \gFo{\quiver{X}} \)-axis is depicted vertically, and the connected components are more easily seen as being intersections of the slab vertices with particular three-dimensional planes:
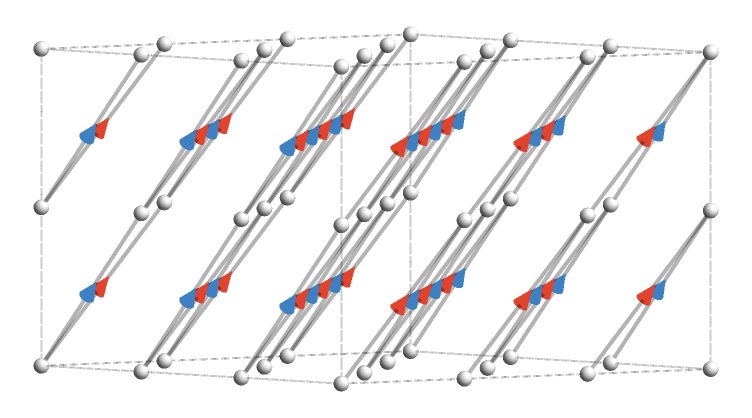
Powers #
We are ready now to consider powers of factors like \( \quiverProdPoly{\reFo{\forwardFactor }},\quiverProdPoly{\reFo{\backwardFactor }} \) allowing terms such as \( \quiverProdPoly{\reFo{\forwardFactor }\,\reFo{\forwardFactor }},\quiverProdPoly{\reFo{\forwardFactor }\,\reFo{\forwardFactor }\,\reFo{\forwardFactor }},\elSy \) and \( \quiverProdPoly{\reFo{\backwardFactor }\,\reFo{\backwardFactor }},\quiverProdPoly{\reFo{\backwardFactor }\,\reFo{\backwardFactor }\,\reFo{\backwardFactor }},\elSy \). We first describe \( \quiverProdPoly{\reFo{\forwardFactor }\,\reFo{\forwardFactor }} \) and consider an example.
For quiver \( \reFo{\quiver{R}} \) we define the monomial \( \quiverProdPoly{\reFo{\forwardFactor }\,\reFo{\forwardFactor }} \) to be the quiver \( \reFo{\quiver{R}_2} \) defined as follows:
\[ \begin{aligned} \vertexList(\reFo{\quiver{R_2}})&\defEqualSymbol \vertexList(\quiver{\reFo{R}})\\ \\ \edgeList(\reFo{\quiver{R_2}})&\defEqualSymbol \setConstructor{\tde{\tvert{r}}{\hvert{r}}{\card{c_1}\cardinalSequenceSymbol \card{c_2}}}{\elemOf{\tde{\tvert{r}}{\vert{m}}{\card{c_1}},\tde{\vert{m}}{\hvert{r}}{\card{c_2}}}{\edgeList(\quiver{\reFo{R}})}}\end{aligned} \]In other words, the product edges of \( \reFo{\quiver{R}_2} \) are 2-paths formed from (non-inverted) factor cardinals in \( \reFo{\quiver{R}} \). The corresponding product cardinals are ordered 2-lists \( \card{c_1}\cardinalSequenceSymbol \card{c_2} \) of the corresponding factor cardinals. This is essentially identical to taking the square of the cardinal adjacency matrix.
Line lattice #
Here is \( \reFo{\quiver{R}_2} \) visualized for \( \reFo{\quiver{R}} = \bindCards{\subSize{\lineQuiver }{6}}{\reFo{\card{r}}} \). It splits into two isomorphic connected components:
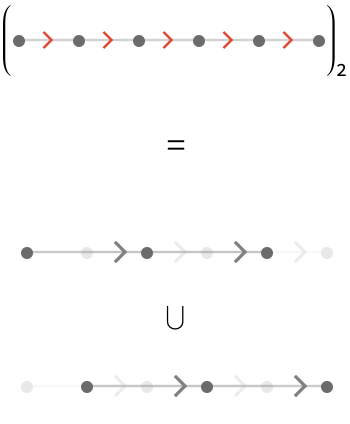
For length \( \reFo{\quiver{R}} = \bindCards{\subSize{\lineQuiver }{5}}{\reFo{\card{r}}} \), the two components are not isomorphic:
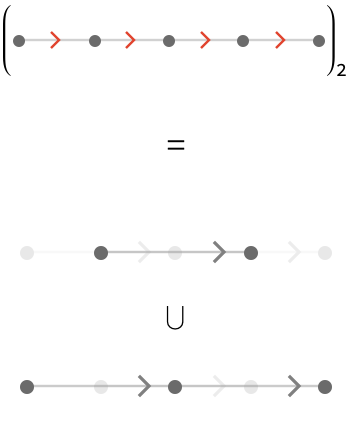
For \( \reFo{\quiver{R}} = \bindCards{\subSize{\cycleQuiver }{6}}{\reFo{\card{r}}} \), we again obtain two connected components:
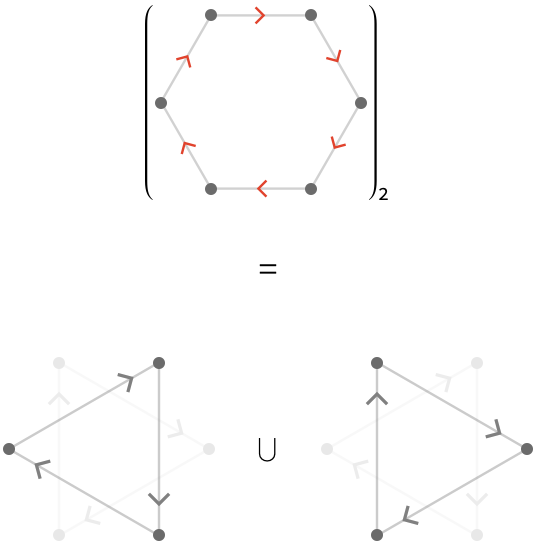
For \( \reFo{\quiver{R}} = \bindCards{\subSize{\cycleQuiver }{5}}{\reFo{\card{r}}} \), we again obtain one connected component:
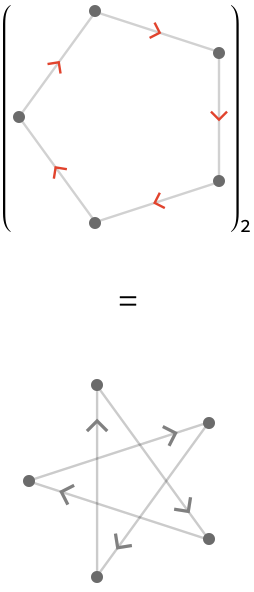
This general pattern is easy to state:
| z | z | z |
|---|---|---|
| finite line quiver | \( \subSize{\lineQuiver }{\sym{n}} \) | \( \subSize{\lineQuiver }{\ceiling{\sym{n} / 2}}\graphUnionSymbol \subSize{\lineQuiver }{\floor{\sym{n} / 2}} \) |
| infinite line quiver | \( \subSize{\lineQuiver }{ \infty } \) | \( \subSize{\lineQuiver }{ \infty }\graphUnionSymbol \subSize{\lineQuiver }{ \infty } \) |
| even cycle quiver | \( \subSize{\cycleQuiver }{2 \, \sym{n}} \) | \( \subSize{\cycleQuiver }{2 \, \sym{n}} \) |
| odd cycle quiver | \( \subSize{\cycleQuiver }{2 \, \sym{n} + 1} \) | \( \subSize{\cycleQuiver }{\sym{n}}\graphUnionSymbol \subSize{\cycleQuiver }{\sym{n}} \) |
Square lattice #
For \( \quiver{Q} \) a square quiver, which has multiple cardinals \( \cardinalList(\quiver{Q}) = \list{\reFo{\card{r}},\blFo{\card{b}}} \), the construction for \( \quiver{Q}_2 \) is a little more complex. Here, the product cardinals are constructed from all possible pairs of non-inverted cardinals:
\[ \cardinalList(\quiver{Q_2}) = \list{\reFo{\card{r}}\cardinalSequenceSymbol \reFo{\card{r}},\reFo{\card{r}}\cardinalSequenceSymbol \blFo{\card{b}},\blFo{\card{b}}\cardinalSequenceSymbol \reFo{\card{r}},\blFo{\card{b}}\cardinalSequenceSymbol \blFo{\card{b}}} \]We visualize \( \quiver{Q}_2 \) for a 5,5-square lattice:
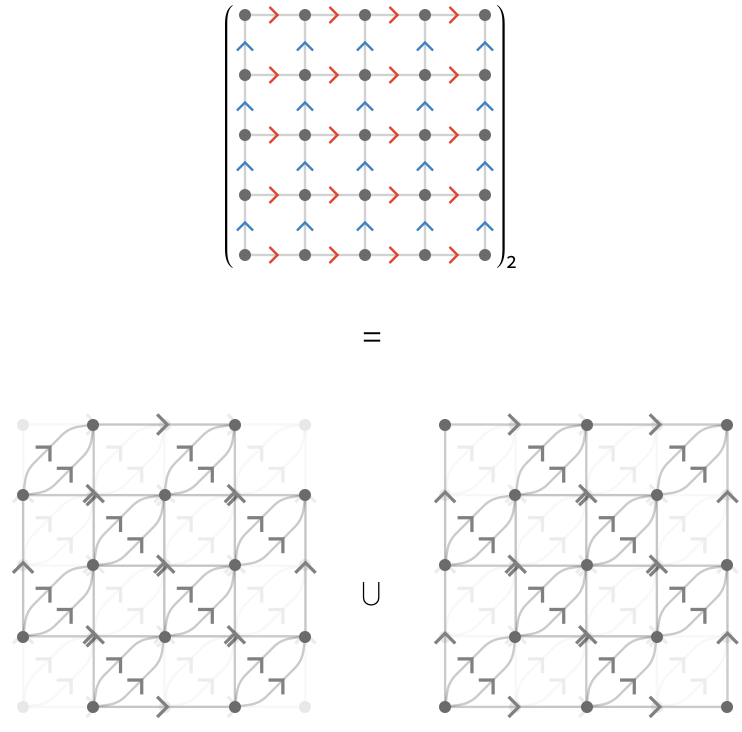
The long horizontal and vertical edges above are the product cardinals \( \reFo{\card{r}}\cardinalSequenceSymbol \reFo{\card{r}} \) and \( \blFo{\card{b}}\cardinalSequenceSymbol \blFo{\card{b}} \), and the short pairs of diagonal edges with identical head and tail are \( \reFo{\card{r}}\cardinalSequenceSymbol \blFo{\card{b}} \) and \( \blFo{\card{b}}\cardinalSequenceSymbol \reFo{\card{r}} \).
Triangular lattice #
The structure of the second power of the triangular lattice is complex and interesting, but will not be described further here.
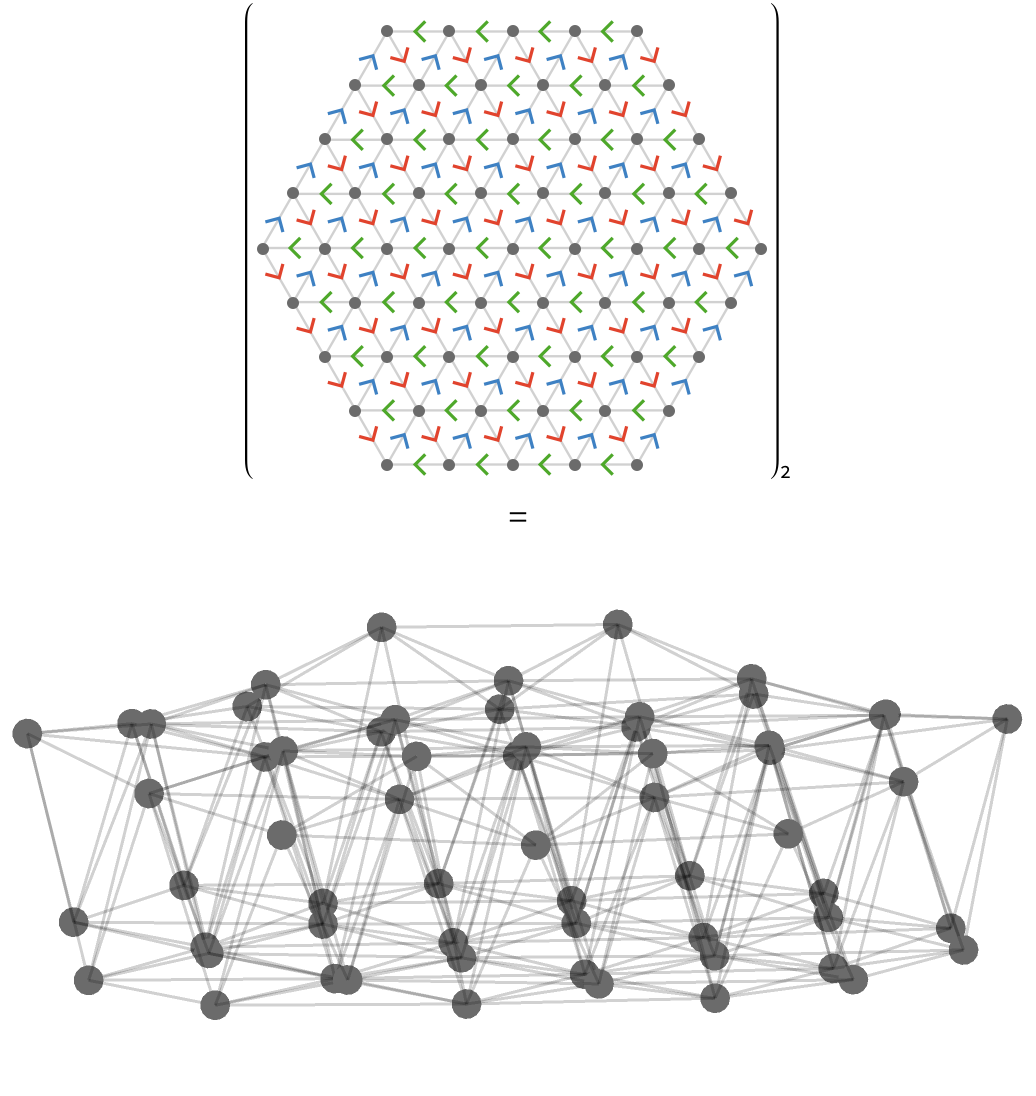
Interaction of \( \forwardFactor \) and \( \backwardFactor \) #

Higher powers #
We can define the general $n^{\textrm{th}}$ forward power of a quiver similarly, written as \( \quiverProdPoly{\quiverProdPower{\reFo{\forwardFactor }}{\sym{n}}}\defEqualSymbol \parenLabeled{\quiverProdPoly{\reFo{\forwardFactor }\,\reFo{\forwardFactor }\,\quiver{\elSy}\,\reFo{\forwardFactor }}}{\sym{n} \maTeFo{ times}} \). The same constructions work as you would imagine for \( \quiverProdPoly{\quiverProdPower{\reFo{\backwardFactor }}{\sym{n}}} \).
