Path quivers #
Recap #
To recap what we accomplished in the previous section: we defined the path groupoid \( \pathGroupoid{\quiver{Q}} \) of a (cardinal) quiver \( \quiver{Q} \), where a path \( \elemOf{\path{P}}{\pathGroupoid{\quiver{Q}}} \) is uniquely determined by its path word \( \paren{\pathWord{\vert{t}}{\wordSymbol{W}}{\vert{h}}} \).
Path quivers #
We’ll now give a way to attach a cardinal structure to the path groupoid \( \pathGroupoid{\quiver{Q}} \), turning it from a groupoid into a quiver, called the path quiver, written \( \pathQuiver{\quiver{Q}} \). We’ll refer to \( \quiver{Q} \) itself as the base quiver.
There will in fact be three kinds of path quiver associated to a base quiver \( \quiver{Q} \):
| z | z |
|---|---|
| \( \pathQuiver{\quiver{Q}} \) | affine path quiver |
| \( \forwardPathQuiver{\quiver{Q}}{\vert{v}} \) | forward path quiver based at vertex \( \vert{v} \) |
| \( \backwardPathQuiver{\quiver{Q}}{\vert{v}} \) | backward path quiver based at vertex \( \vert{v} \) |
For the forward and backward path quivers, \( \vert{v} \) is an arbitrary vertex in \( \quiver{Q} \) which we will call the origin or base point. Therefore there is a family of quivers \( \forwardPathQuiver{\quiver{Q}}{\vert{v}} \), \( \backwardPathQuiver{\quiver{Q}}{\vert{v}} \) given by choices of \( \elemOf{\vert{v}}{\vertexList(\quiver{Q})} \). In contrast, there is only one affine path quiver \( \pathQuiver{\quiver{Q}} \).
Forward path quiver #
We'll start with the forward path quiver. It is defined as follows:
\[ \begin{aligned} \vertexList(\forwardPathQuiver{\quiver{Q}}{\vert{x}})&\defEqualSymbol \pathList(\quiver{Q},\vert{x},\blSy)\\ \\ \edgeList(\forwardPathQuiver{\quiver{Q}}{\vert{x}})&\defEqualSymbol \setConstructor{\tde{\path{P}}{\path{R}}{\card{c}}}{\pathCompose{\path{P}}{\card{c}} = \path{R}}\end{aligned} \]Expressing this in words, we say that a vertex of \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) is a path \( \path{P} \) in \( \quiver{Q} \) starting at the base vertex \( \vert{x} \), and an edge of \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) is \( \tde{\path{P}}{\path{R}}{\card{c}} \) , where \( \path{P} \) is a path that can be extended by the cardinal \( \elemOf{\card{c}}{\cardinalList(\quiver{Q})} \) to give the path \( \path{R} \).
Essentially, the forward path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) "trees out" all paths in \( \quiver{Q} \) that can be constructed starting at vertex \( \vert{x} \).
Example: 2-bouquet quiver #
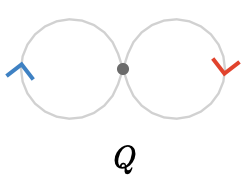
The idea is most intuitive when presented visually. We’ll show the path quiver for a base quiver \( \quiver{Q} = \bindCards{\bouquetQuiver{2}}{\reFo{\card{r}},\blFo{\card{b}}} \), namely a 2-bouquet quiver on cardinals \( \reFo{\card{r}} \) then \( \blFo{\card{b}} \). We'll refer to the single vertex of \( \quiver{Q} \) as \( \vert{x} \).
Here we show a fragment of the infinite forward path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \). Each vertex will be illustrated with the path that it represents.
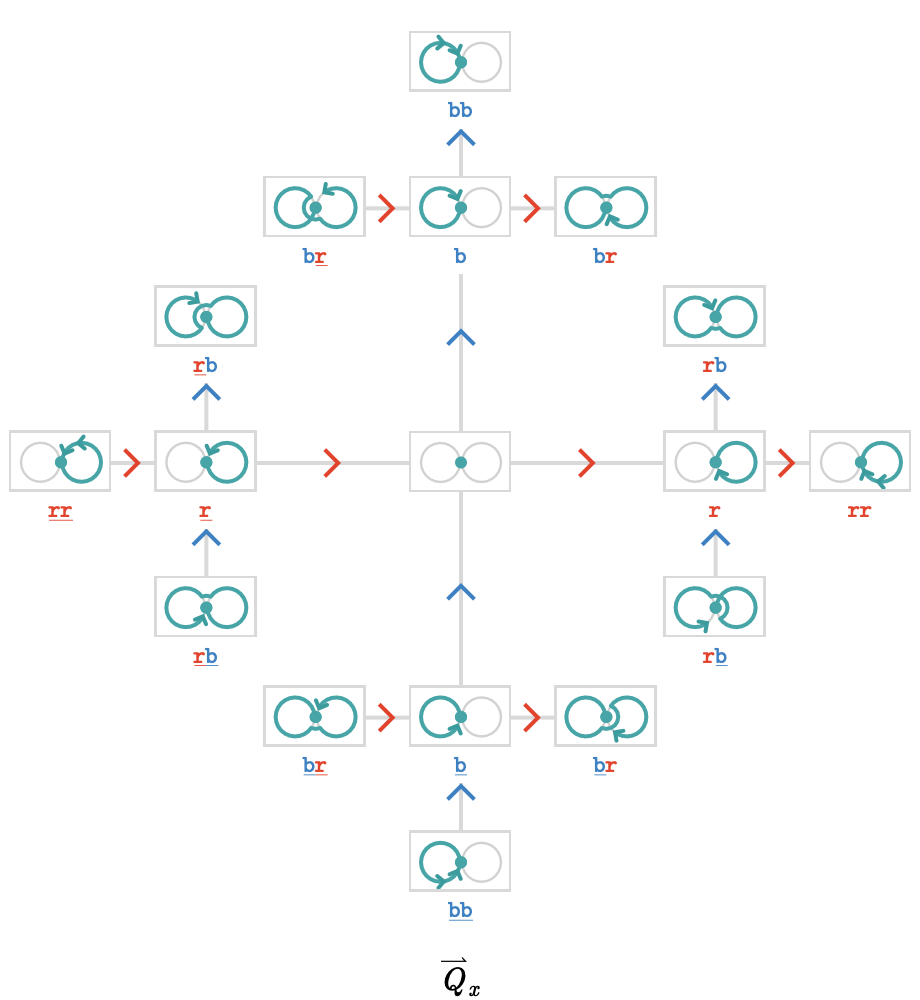
This is already a complex example, so studying this visualization carefully is instructive.
Notice that the "origin vertex" in \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) is the empty path, shown in the center as a copy of \( \quiver{Q} \) with a teal dot, having path word \( \paren{\pathWord{\vert{x}}{\emptyWord{}}{\vert{x}}} \). This empty path is the unit \( \identityElement{x} \) in the path groupoid.
To understand the nature of the path quiver, we’ll focus on the origin, representing the empty path \( \paren{\pathWord{\vert{x}}{\emptyWord{}}{\vert{x}}} \):
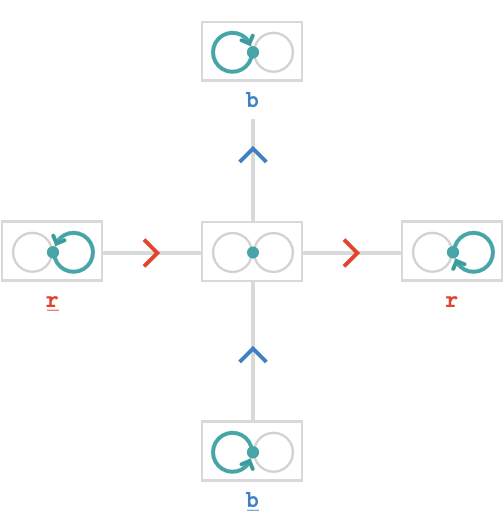
We can extend the empty path \( \parenPathWord{\vert{x}}{\emptyWord{}}{\vert{x}} \) in four ways: taking \( \reFo{\card{r}} \) gives us the "east" vertex \( \parenPathWord{\vert{x}}{\word{\reFo{\ncard{r}}}}{\vert{x}} \), taking \( \blFo{\card{b}} \) gives us the "north" vertex \( \parenPathWord{\vert{x}}{\word{\blFo{\card{b}}}}{\vert{x}} \). If we instead take the inverted cardinals \( \reFo{\inverted{\card{r}}} \) or \( \blFo{\inverted{\card{b}}} \) we obtain paths that traverse the underlying edges in the anticlockwise direction: taking \( \reFo{\inverted{\card{r}}} \) gives us the "west" vertex \( \parenPathWord{\vert{x}}{\word{\reFo{\ncard{r}}}}{\vert{x}} \), taking \( \blFo{\inverted{\card{b}}} \) gives us the "south vertex“ \( \parenPathWord{\vert{x}}{\word{\blFo{\ncard{b}}}}{\vert{x}} \).
Let's now examine another section of \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) centered on the east vertex:
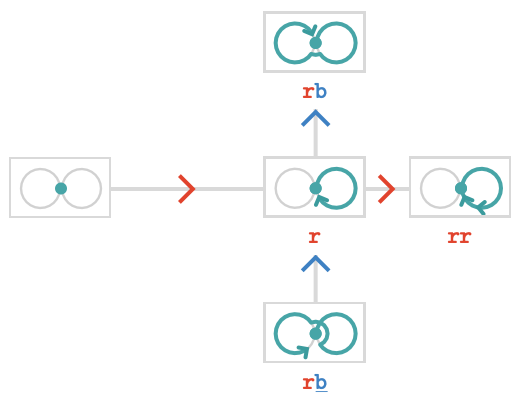
Taking \( \reFo{\card{r}} \) again from \( \paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}}{\vert{x}}} \) gives the "east east" vertex \( \paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}{\reFo{\card{r}}}}{\vert{x}}} \), illustrated as a loop with a double arrowhead. Taking \( \blFo{\card{b}} \) gives the "north east" vertex \( \paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}{\blFo{\card{b}}}}{\vert{x}}} \), in which we first loop clockwise around the \( \reFo{\card{r}} \) cycle and then clockwise around the \( \blFo{\card{b}} \) cycle. Taking \( \blFo{\inverted{\card{b}}} \) gives the "south east" vertex \( \paren{\pathWord{\vert{x}}{\word{\reFo{\card{r}}}{\blFo{\ncard{b}}}}{\vert{x}}} \), which loops anticlockwise around the \( \blFo{\card{b}} \) cycle instead. Taking \( \reFo{\inverted{\card{r}}} \) backtracks to the empty path we've already seen.
Extension and retraction #
Notice that we can and should interpret "extend path by \( \reFo{\card{r}} \)" as the inverse operation to "extend path by \( \reFo{\inverted{\card{r}}} \)", since the sub-word \( \word{\reFo{\card{r}}}{\reFo{\ncard{r}}} \) is formally equal to the empty sub-word, and can be removed from any word. Hence when a path word ends in an \( \reFo{\card{r}} \), "extend path by \( \reFo{\inverted{\card{r}}} \)" is equivalent to "retract path by \( \reFo{\card{r}} \)".
Tree structure #
You may have noticed that \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) is in fact a tree, rooted at the empty path. This is because a vertex in \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \), which is a path in \( \quiver{Q} \), is uniquely determined by its path word, and there is only one way of extending the empty path word \( \paren{\pathWord{\vert{x}}{\emptyWord{}}{\vert{x}}} \) by individual cardinals to obtain this path word. Seen as a graph, this quiver is sometimes known as a Bethe lattice or regular tree.
We can generalize this observation with the following theorem:
\[ \forwardPathQuiver{\bouquetQuiver{\sym{k}}}{\vert{}}\isomorphicSymbol \treeQuiver{\sym{k}} \]In English, this is the statement that forward path quiver of a \( \sym{k} \)-bouquet quiver is an infinite \( \sym{k} \)-tree quiver on the same cardinals.
Example: 2-line quiver #
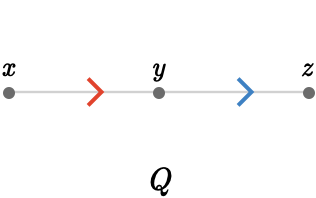
The path quiver need not be infinite. Let's consider the quiver \( \quiver{Q} = \bindCards{\subSize{\lineQuiver }{2}}{\reFo{\card{r}}\serialCardSymbol \blFo{\card{b}}} \). We'll label the vertices \( \vert{x} \), \( \vert{y} \), \( \vert{z} \).
Here is the path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \):
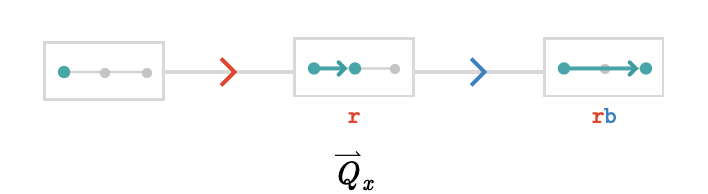
This path quiver is not only finite, it is isomorphic to the original quiver! In general, this will occur whenever the quiver is a tree, since there is then only one path from the origin (wherever we choose it) to every other vertex.
We’ve seen \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \), but let’s examine how it compares to \( \forwardPathQuiver{\quiver{Q}}{\vert{y}} \) and \( \forwardPathQuiver{\quiver{Q}}{\vert{z}} \):
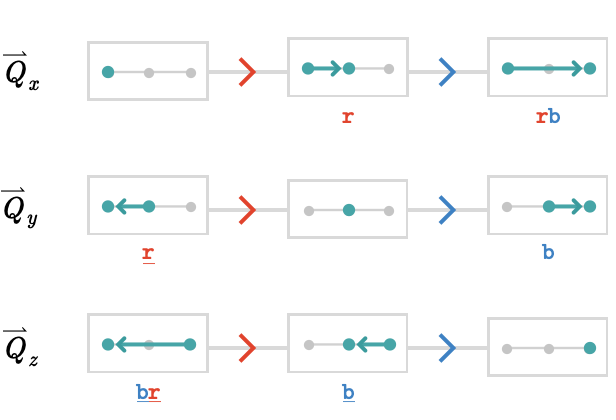
As you can see, these are all isomorphic, and the choice of origin is in some sense irrelevant. We can summarize this observation with the following theorem (the base vertex is not shown here, as it is irrelevant):
\[ \forwardPathQuiver{\subSize{\lineQuiver }{\sym{n}}}{\vert{}}\isomorphicSymbol \subSize{\lineQuiver }{\sym{n}} \]Example: finite tree #
The fact that a tree quiver is isomorphic to its forward path quivers can be surprising at first. Let's illustrate this isomorphism for a more elaborate tree, with root vertex \( \vert{0} \):
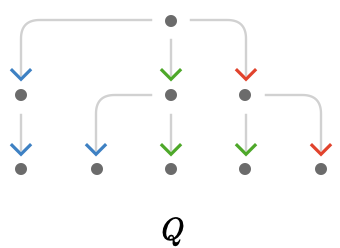
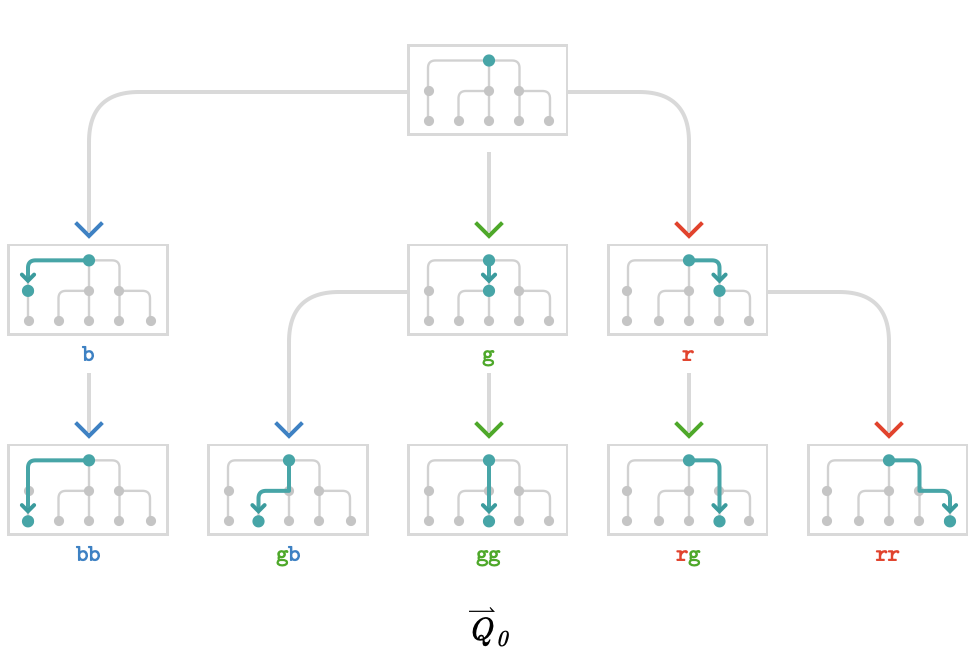
Again, notice that the cardinal structure of the base quiver \( \quiver{Q} \) is mirrored exactly by the structure of the path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{0}} \).
This fact is also true of the transitive trees we defined in the Transitive quivers (again, the base vertex is not shown, and taken to be the center of the tree):
\[ \forwardPathQuiver{\subSize{\treeQuiver{\sym{k}}}{\sym{n}}}{\vert{}}\isomorphicSymbol \subSize{\treeQuiver{\sym{k}}}{\sym{n}} \]Example: 2-cycle quiver #
For now, we’ll conclude this section by looking at the quiver \( \quiver{Q} = \bindCards{\subSize{\cycleQuiver }{2}}{\reFo{\card{r}}\serialCardSymbol \blFo{\card{b}}} \) with vertices \( \vert{x} \), \( \vert{y} \):
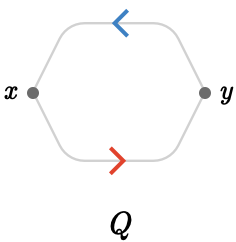
The path quiver structure is much simpler than for the 2-bouquet quiver, because the once a path is non-empty, it can only be extended in one possible way.
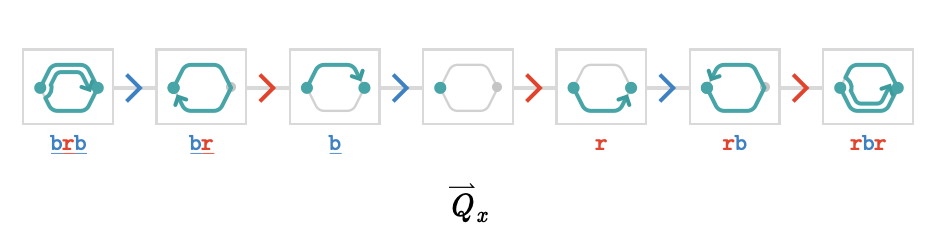
This path quiver is a bi-infinite linear chain, starting at the empty path in the middle. Here, a path must take the cardinals \( \reFo{\card{r}} \), \( \blFo{\card{b}} \) in alternating fashion, but it can wind clockwise, giving the (infinite) left side of the chain, or anticlockwise, giving to the (infinite) right side.
For a general \( \sym{n} \)-cycle quiver, we have the following theorem (modulo base vertex):
\[ \forwardPathQuiver{\subSize{\cycleQuiver }{\sym{n}}}{\vert{}}\isomorphicSymbol \subSize{\lineQuiver }{ \infty } \]Fundamental cycles #
When a cycle is present in a finite quiver, then it is easy to see that the corresponding path quiver will be infinite: the presence of cycles guarantees the path quiver will be infinite, because we can make arbitrarily long paths by traversing the cycle repeatedly. One way to understand this is to consider only the fundamental cycles of the quiver: these are cycles that form a sub-path of any larger cycle. Any infinite path must contain these fundamental cycles as sub-paths infinitely many times (traversed in an appropriate order). So far we haven’t been too precise about what defines such a fundamental cycle, and in fact there is some freedom in how they are defined that is analogous to the choice of a basis in a vector space, so we will return to this topic when we have the requisite mathematical machinery.
Grid quiver #
For now, we can observe that for the infinite grid quiver \( \subSize{\gridQuiver{\sym{k}}}{ \infty } \), we can extend the empty path in exactly \( 2 \, \sym{k} \) ways (the cardinals and their inverses), and we can extend a non-empty path in exactly \( 2 \, \sym{k} - 1 \) distinct ways to avoid backtracking. Since we cannot extend two distinct paths to yield the same path, the path quiver is necessarily a tree. Therefore, we have the following theorem:
\[ \forwardPathQuiver{\subSize{\gridQuiver{\sym{k}}}{ \infty }}{\vert{}}\isomorphicSymbol \subSize{\treeQuiver{\sym{k}}}{ \infty } \]The situation for a finite grid quiver is more complex, as the number of ways we can extend a path depends on which vertex we are on the base quiver: there could be between \( \sym{k} - 1 \) and \( 2 \, \sym{k} - 1 \) possible extensions. For example, on a finite line quiver, there is 1 possible extension for an interior vertex, and 0 possible extensions on the two edge vertices. On a square quiver, there are 3 possible extensions for an interior vertex, 2 possible extensions for an edge vertex, and only 1 possible extension for the 4 corner vertices.
Backward path quiver #
Intuition #
We constructed the forward path quiver \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \) by successively extending the empty path \( \paren{\pathWord{x}{\emptyWord{}}{x}} \) on the right, yielding edges of the form:
\[ \tde{\parenPathWord{\vert{x}}{\wordSymbol{W}}{\vert{y}}}{\parenPathWord{\vert{x}}{\concat{\wordSymbol{W} \word{\card{c}}}}{\vert{z}}}{\card{c}} \]We can perform a mirror construction to this, where we instead extending the empty path \( \paren{\pathWord{x}{\emptyWord{}}{x}} \) on the left, yielding edges of the form:
\[ \tde{\parenPathWord{\vert{y}}{\wordSymbol{W}}{\vert{x}}}{\parenPathWord{\vert{y}}{\concat{\word{\card{c}} \wordSymbol{W}}}{\vert{x}}}{\mcard{c}} \]Notice that the cardinal labeling this edge is \( \mcard{c} \), which we call a mirror cardinal. It is distinct from \( \card{c} \) itself.
The resulting path quiver is called the backward path quiver \( \backwardPathQuiver{\quiver{Q}}{\vert{x}} \), and shares the same vertices as \( \forwardPathQuiver{\quiver{Q}}{\vert{x}} \), since extending the empty path on the left by \( \mcard{c} \) yields the same path as extending it on the right by \( \inverted{\card{c}} \).
Definition #
More formally, we can write \( \backwardPathQuiver{\quiver{Q}}{\vert{x}} \) as:
\[ \begin{aligned} \vertexList(\backwardPathQuiver{\quiver{Q}}{\vert{x}})&\defEqualSymbol \pathList(\quiver{Q},\blSy,\vert{x})\\ \\ \edgeList(\backwardPathQuiver{\quiver{Q}}{\vert{x}})&\defEqualSymbol \setConstructor{\tde{\path{P}}{\path{R}}{\mcard{c}}}{\pathCompose{\card{c}}{\path{P}} = \path{R}}\end{aligned} \]Affine path quiver #
The utility of considering both the forward and backward path quivers is that they allow us to construct the affine path quiver \( \pathQuiver{\quiver{Q}} \).
While the forward and backward path quivers depend on a choice of base vertex, the affine path quiver does not. It is constructed as follows:
\[ \begin{aligned} \vertexList(\pathQuiver{\quiver{Q}})&\defEqualSymbol \pathList(\quiver{Q},\blSy,\blSy)\\ \\ \edgeList(\pathQuiver{\quiver{Q}})&\defEqualSymbol \begin{nsarray}{c} \setConstructor{\tde{\path{P}}{\path{R}}{\card{c}}}{\pathCompose{\path{P}}{\card{c}} = \path{R}}\\ \cup \\ \setConstructor{\tde{\path{P}}{\path{R}}{\mcard{c}}}{\pathCompose{\card{c}}{\path{P}} = \path{R}} \end{nsarray} \end{aligned} \]Expressing this in words, we say a vertex of \( \pathQuiver{\quiver{Q}} \) is a path \( \path{P} \) in \( \quiver{Q} \), and an edge of \( \pathQuiver{\quiver{Q}} \) is either:
-
\( \tde{\path{P}}{\path{R}}{\card{c}} \) , where \( \path{P} \) is a path that can be extended on the right by the cardinal \( \elemOf{\card{c}}{\cardinalList(\quiver{Q})} \) to give the path \( \path{R} \)
-
\( \tde{\path{P}}{\path{R}}{\mcard{c}} \) , where \( \path{P} \) is a path that can be extended on the left by the cardinal \( \elemOf{\card{c}}{\cardinalList(\quiver{Q})} \) to give the path \( \path{R} \)
Connectedness #
An important fact about the affine path quiver \( \pathQuiver{\quiver{Q}} \) is that it is connected iff the quiver \( \quiver{Q} \) is connected. Why is this?
Consider two vertices \( \path{P},\path{R} \) of \( \pathQuiver{\quiver{Q}} \), corresponding to paths in \( \quiver{Q} \) as follows:
\[ \path{P} = \parenPathWord{\tvert{\vert{p}}}{\wordSymbol{P}}{\hvert{\vert{p}}}\quad \path{R} = \parenPathWord{\tvert{\vert{r}}}{\wordSymbol{R}}{\hvert{\vert{r}}} \]Clearly there is a path in \( \pathQuiver{\quiver{Q}} \) connecting \( \path{P} \) to \( \paren{\pathWord{\hvert{p}}{\emptyWord{}}{\hvert{p}}} \), given by retractions on the left according to the cardinals of \( \wordSymbol{P} \). Similarly there is a path connecting \( \path{R} \) to \( \paren{\pathWord{\tvert{r}}{\emptyWord{}}{\tvert{r}}} \), given by retractions on the right according to the cardinals of \( \wordSymbol{R} \). Lastly, since \( \quiver{Q} \) is connected there is at least one path \( \paren{\pathWord{\hvert{p}}{\wordSymbol{S}}{\tvert{r}}} \) in \( \quiver{Q} \) , which implies a path in \( \pathQuiver{\quiver{Q}} \) connecting \( \paren{\pathWord{\hvert{p}}{\emptyWord{}}{\hvert{p}}} \) to \( \paren{\pathWord{\hvert{p}}{\wordSymbol{S}}{\tvert{r}}} \) by extension on the right, or if we prefer a path connecting \( \paren{\pathWord{\tvert{r}}{\emptyWord{}}{\tvert{r}}} \) to \( \paren{\pathWord{\hvert{p}}{\wordSymbol{S}}{\tvert{r}}} \) by extension on the left. Therefore we have a path connecting \( \path{P} \) to \( \path{R} \), specifically:
\[ \parenPathWord{\parenPathWord{\tvert{\vert{p}}}{\wordSymbol{P}}{\hvert{\vert{p}}}}{\concat{\inverted{\mirror{\wordSymbol{P}}} \wordSymbol{S} \wordSymbol{R}}}{\parenPathWord{\tvert{\vert{r}}}{\wordSymbol{R}}{\hvert{\vert{r}}}} \]Visualization #
We'll focus on the following base quiver:

Here we show the forward path quivers and backward path quivers side-by-side:

Summary #
We've defined the forward, backward, and affine path quivers. The forward path quiver will be most useful in the sections that follow.
We also saw examples, and inferred the following general relationships:
| base quiver | forward path quiver |
|---|---|
| \( \bouquetQuiver{\sym{k}} \) | \( \subSize{\treeQuiver{\sym{k}}}{ \infty } \) |
| \( \subSize{\lineQuiver }{\sym{n}} \) | \( \subSize{\lineQuiver }{\sym{n}} \) |
| \( \subSize{\treeQuiver{\sym{k}}}{\sym{n}} \) | \( \subSize{\treeQuiver{\sym{k}}}{\sym{n}} \) |
| \( \subSize{\cycleQuiver }{\sym{n}} \) | \( \subSize{\lineQuiver }{ \infty } \) |
| \( \subSize{\gridQuiver{\sym{k}}}{ \infty } \) | \( \subSize{\treeQuiver{\sym{k}}}{ \infty } \) |