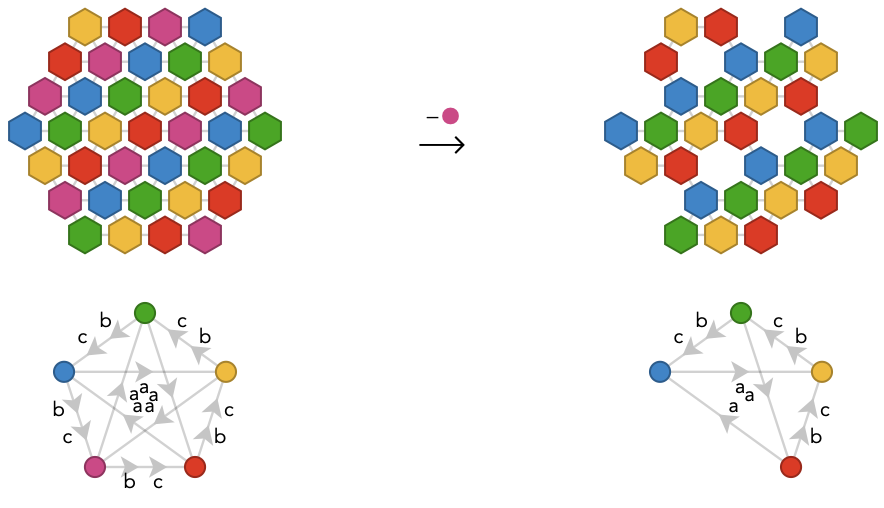Vertex colorings #
Introduction #
Returning to colorings, we are now better equipped to understand how colorings correspond to coverings. We say a quiver covering \( \functionSignature{\pathHomomorphism{ \pi }}{\quiver{G}}{\quiver{H}} \) induces a coloring of \( \quiver{G} \), where the “colors” are just the identities of vertices in \( \quiver{H} \). In other words, the color of a vertex \( \elemOf{\vert{g}}{\vertexList(\quiver{G})} \) is simply which vertex \( \elemOf{\vert{h}}{\vertexList(\quiver{H})} \) it is sent to: specifically \( \vert{h} = \graphHomomorphism{ \pi _{\vertices{}}}(\vert{g}) \). We can of course only use visible colors to illustrate this idea when \( \quiver{H} \) has a finite number of vertices.
What makes this covering perspective on colorings interesting is that there is a fairly mechanical process we can use to construct finite coverings of any fundamental quiver. These coverings will continue to generate the same lattice quiver as the original fundamental quiver, but will yield colorings of the lattice quiver containing more colors. We’ll see later that that the families of colorings given by fundamental coverings are in a sense discrete harmonics of a particular lattice quiver, generated by discrete partial difference equations.
Line lattice #
Let’s look first at the 1-dimension line lattice.
The fundamental coloring given by the simplest fundamental quiver, the bouquet quiver, is a 1-coloring (or constant coloring), since the bouquet only has one vertex:
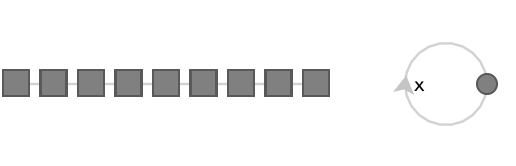
Here’s the 2-coloring, given by the fundamental quiver that simply alternates between the two colors:

Higher colorings are given by “circle quivers” with more vertices, where the cardinal simply cycles among the colors (the 1- and 2-colorings can be seen as instances of these):
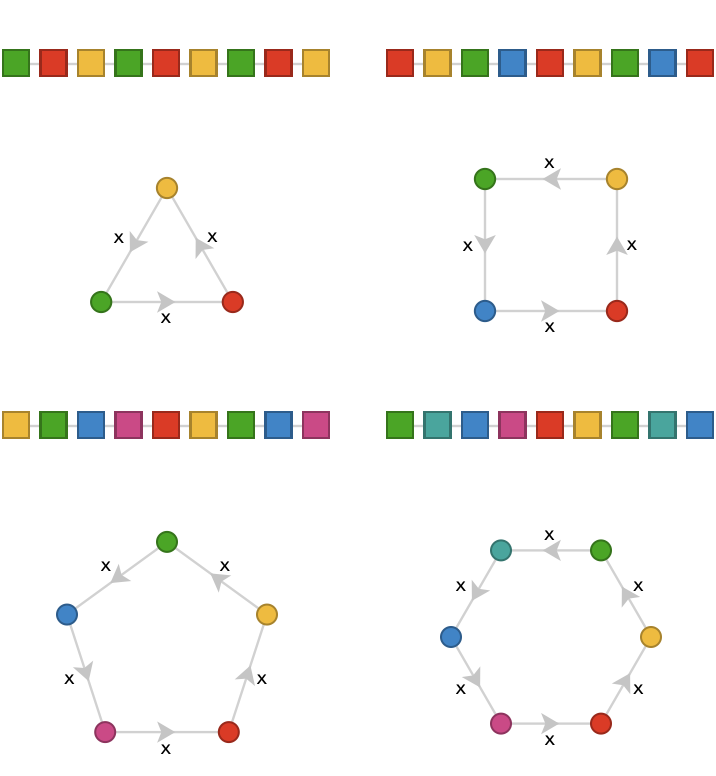
These are the only fundamental colorings of the line lattice, since there is no remaining freedom for how to choose cardinals once the number of vertices in the fundamental quiver is decided.
Square lattice #
The square lattice brings with it more interesting behavior, since the two cardinals can interact in various ways. But let’s start with the 1-coloring given by the simplest fundamental quiver:

With two colors, we obtain “stripes” of constant color that are horizontally, vertically, or diagonally oriented:
3-colorings display a similar pattern, except the diagonal stripes can now be oriented in two different ways (whereas in the case of 2 colors, both of these orientations yield the same coloring):
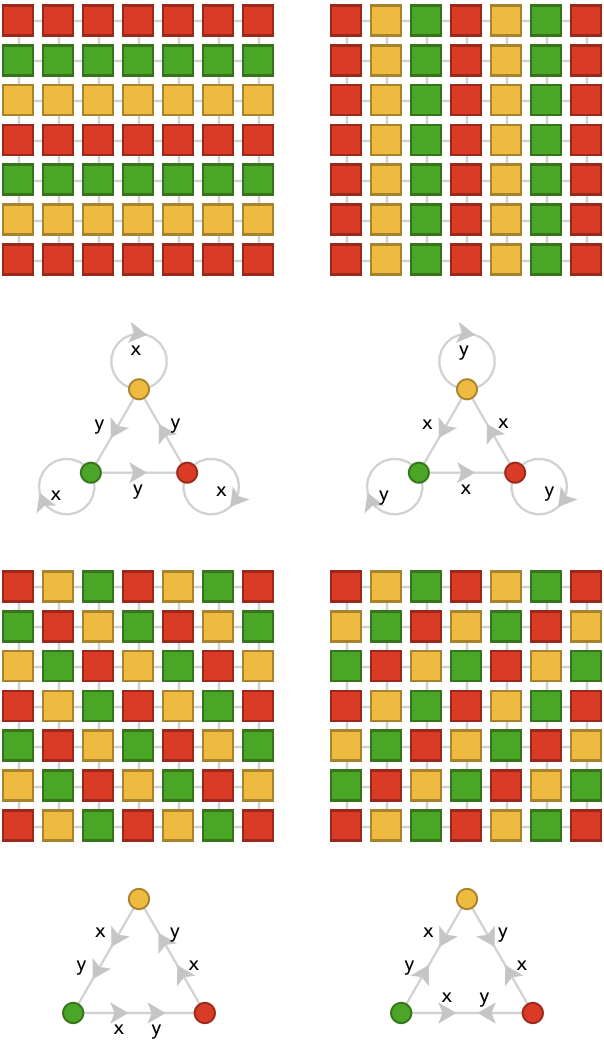
4-colorings repeat these motifs, but include a third kind of behavior we haven’t encountered before, in which fixing a color yields a “decimated” form of the original square lattice at one-quarter resolution:
One way we can view these colorings is as embedding sub-lattices in the quiver lattice. The idea is to choose a color in the fundamental quiver and consider the set of (shortest) paths that begin and end at this vertex. The words for these paths then act as the primitive cardinals for the sub-lattice. The first four colorings above yield to the line lattice by choosing e.g. blue, and the path words \( \word{\card{x}} \), \( \word{\card{y}} \), and \( \word{\card{x}}{\ncard{y}} \) respectively. The fifth coloring yields the square lattice, via blue and the path words \( \list{\word{\card{x}}{\card{x}},\word{\card{y}}{\card{y}}} \).
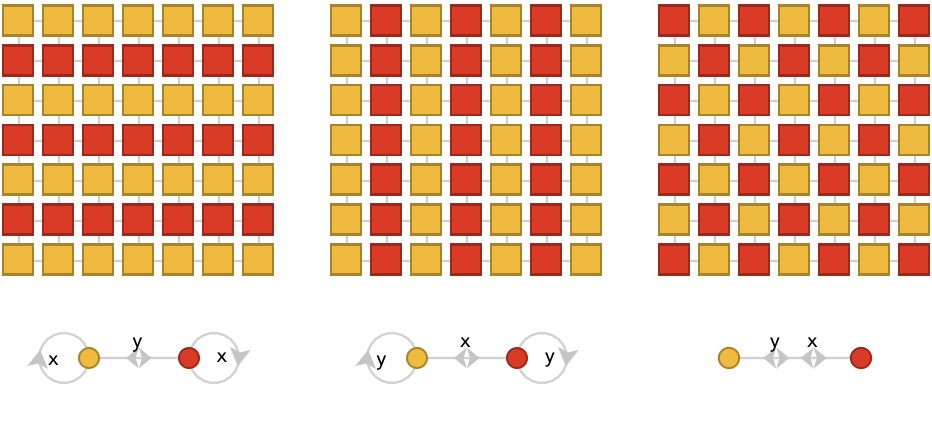
Let's call this fifth coloring a 1-decimation, since it is the smallest possible decimation. A 2-decimation is shown below, with path words \( \list{\word{\card{x}}{\card{x}}{\card{x}},\word{\card{y}}{\card{y}}{\card{y}}} \):
Triangular lattice #
Let’s now turn to colorings of the triangular lattice. As before, we’ll start with the 1*-*coloring induced by the simplest fundamental quiver:
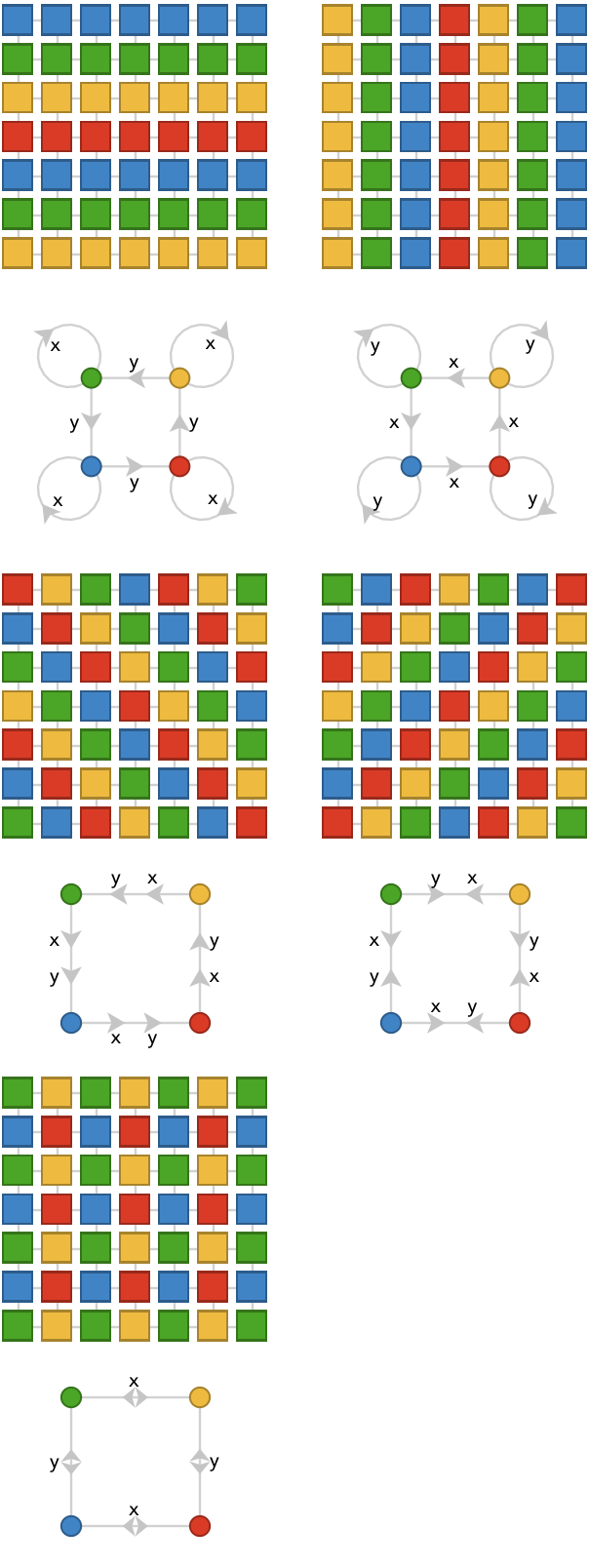
The two-colorings are the familiar oriented stripes, which can now occur along the three cardinal axes. Interestingly, there is no equivalent of the diagonal stripes we saw in the square case:
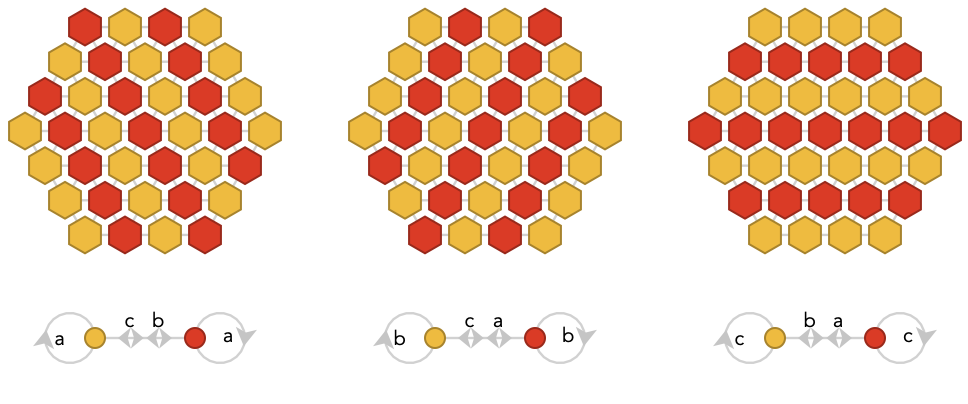
The 3-colorings do include a new motif that can be seen either as 1-decimation of the triangular lattice, or as a diagonal stripe that is half-way between the orientations of the 3 cardinals. Again, as in the square case, this single coloring simultaneously yields all 3 orientations of this diagonal in a “degenerate” way:
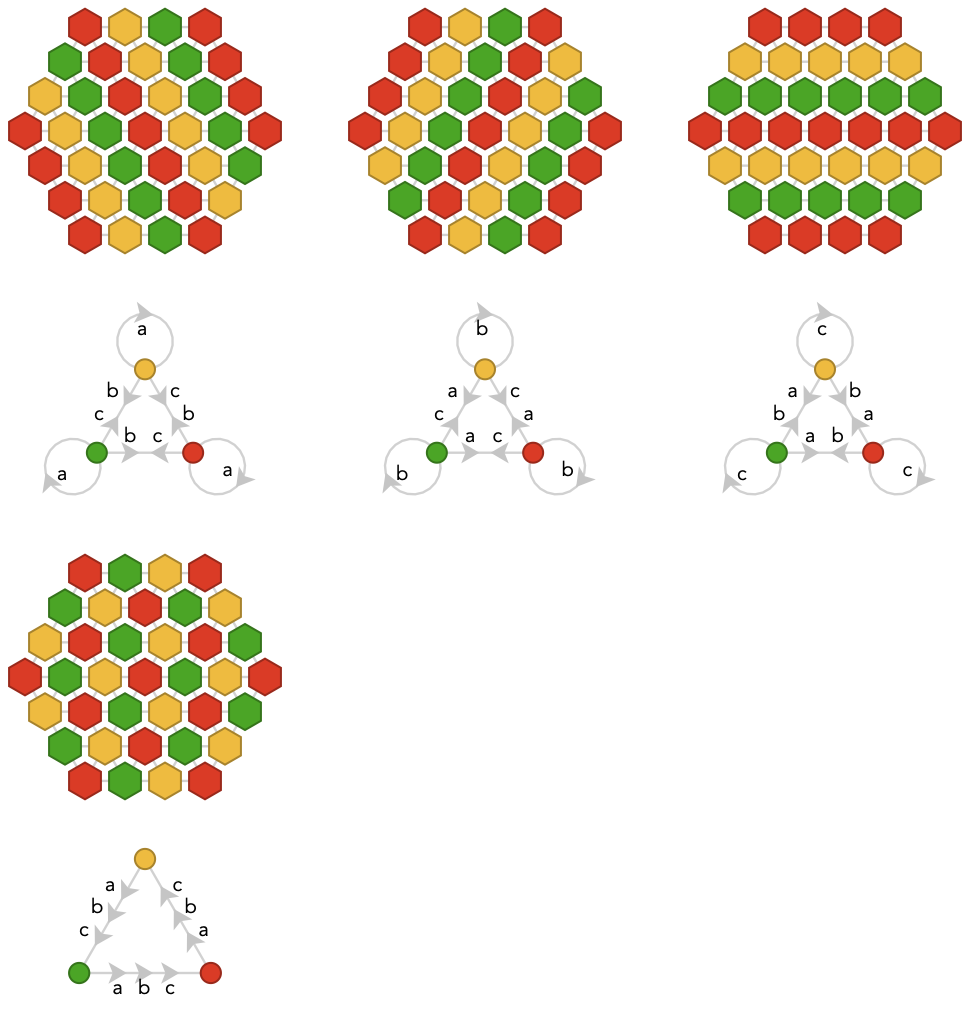
As we saw before in the square case, moving to 4-colorings causes the single degenerate diagonal coloring to split into oriented versions:
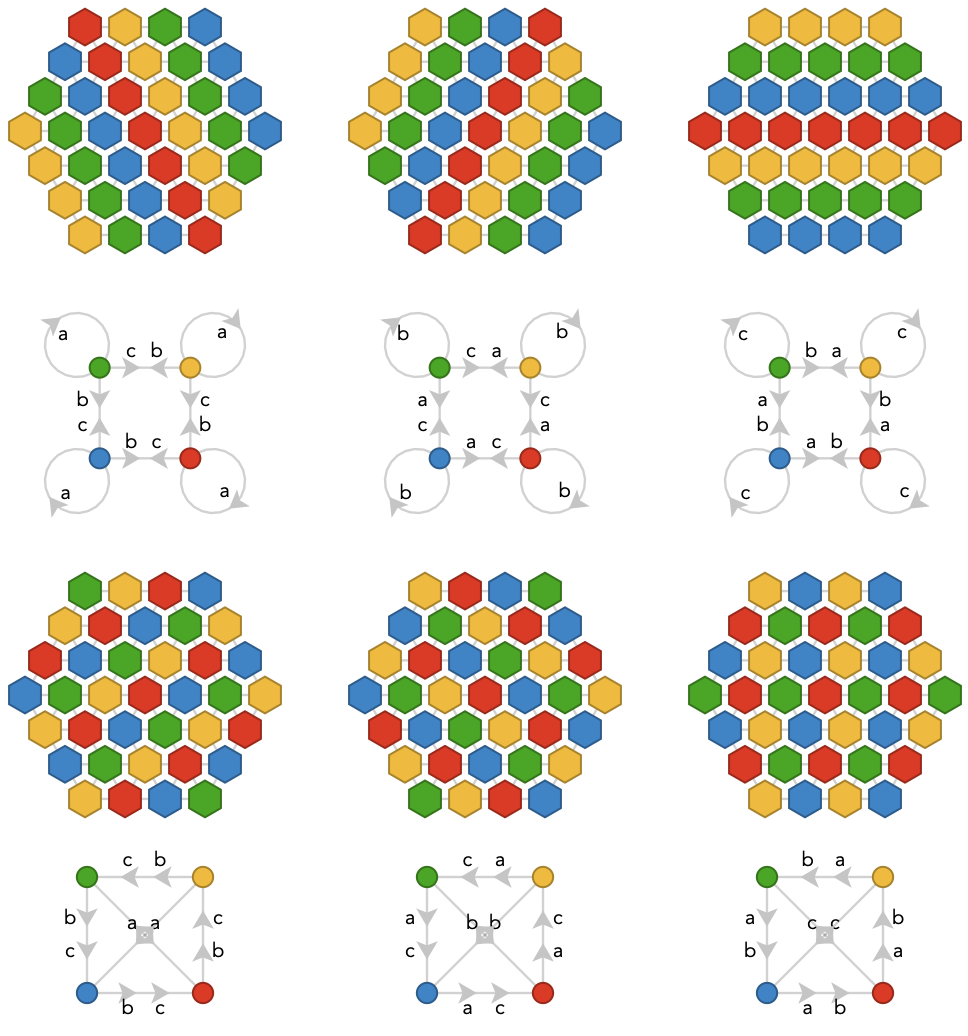
With 5-colorings, this situation repeats unchanged:
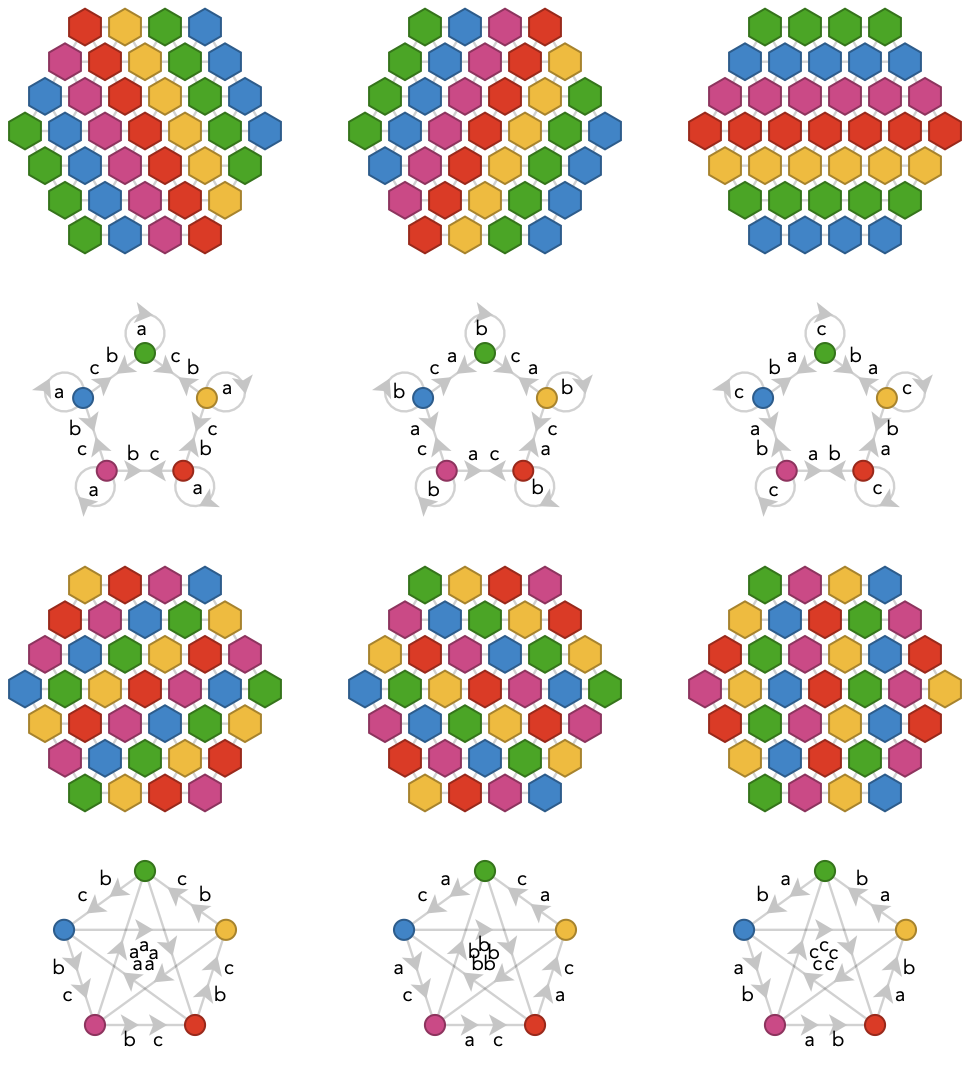
Jumping ahead to 9-colorings, we obtain a 2-decimation of the triangular lattice to itself:
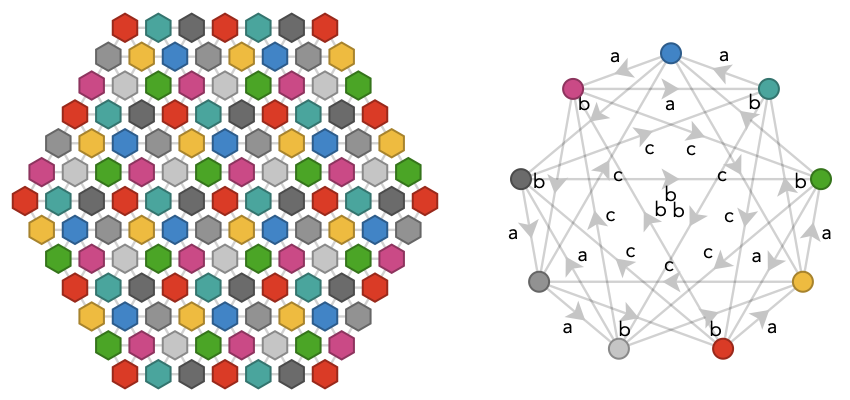
This 2-decimation is in fact almost identical to the 2-decimation of the square lattice we saw earlier, thanks to the fact that a triangular lattice can be obtained from a square lattice by introducing additional edges that connect each vertex \( \vert{v} \) to the vertex \( \vert{w} \) via path \( \pathWord{\vert{v}}{\word{\card{x}}{\card{y}}}{\vert{w}} \).
It’s not hard to see that for both triangular and square lattices, an \( n \)-decimation has \( (n+1)^2 \) colors.
Hexagonal lattice #
The hexagonal lattice, being the first lattice with a non-bouquet fundamental quiver, generally requires many more colors in its fundamental quivers, making its analysis more cumbersome.
Let's start with the smallest fundamental quiver, which is already a two-coloring:
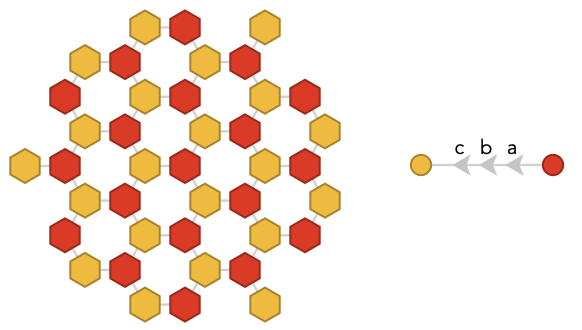
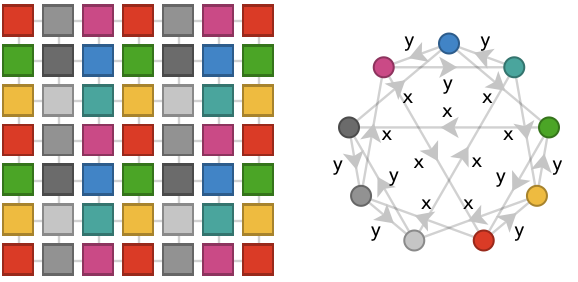
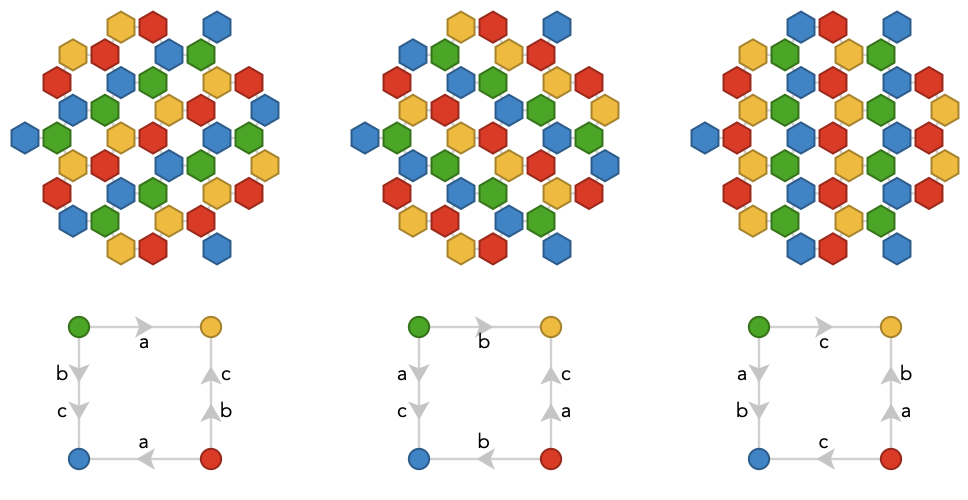
There are no three colorings. Four-colorings produce “mixed diagonal” stripes composed of two colors and two cardinals taken in alternation:
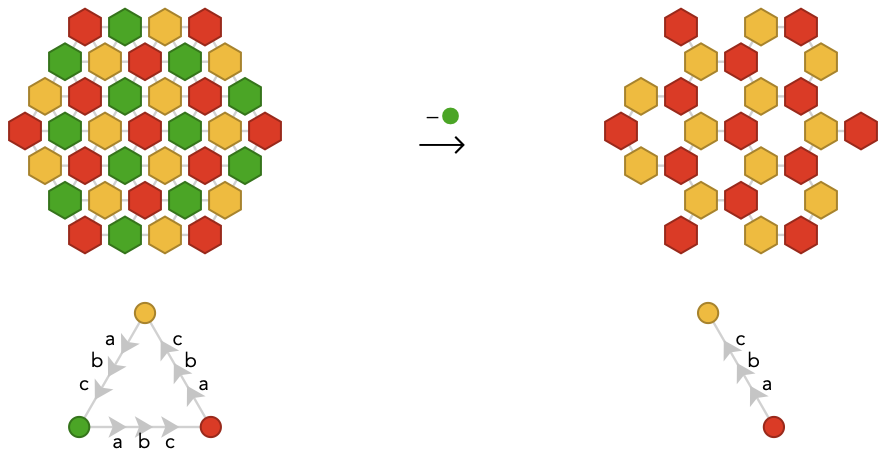
There is a simple connection between \( n \)-colorings of the hexagonal lattice and \( n+1 \)-colorings of triangular lattice: observe that the hexagonal lattice can be obtained from the triangular lattice by deleting a certain set of vertices, leaving a triangular pattern of “holes”. We can achieve this by deleting one or more vertices from the fundamental quiver of a triangular lattice if those vertices yield the right triangular pattern of holes. This will give a fundamental quiver that generates the hexagonal lattice, and hence a hexagonal lattice coloring. For example, the 2-coloring shown above can be obtained from the 1-decimation of the square lattice by deleting the green fundamental vertex:
Similarly we can obtain of the hexagonal 4-colorings by deleting a color from triangular 5-colorings. Here we show one case: