Introduction #
This site describes an incomplete and ongoing project to build a discrete, computational framework for geometry, using "off the shelf" components from a range of mathematical fields, including graph theory, group theory, abstract algebra, representation theory, theoretical computer science, differential geometry, calculus, and others.
It asks the questions: how are we to think about geometries that have a "smallest scale"? And how do we represent geometries that are produced by computational processes?
Novelty #
None of the conceptual tools developed in this work are on their own very novel, although their assembly and emphasis into a unifying whole might prove to be for some readers. A theory is as much a way of seeing as it is a body of theorems, and so the approach I am pursuing hopes to offer a way of recasting and re-interpreting existing structures to emphasize a more computational and geometric perspective.
Visualization #
One of my aims is to render intuitive this approach to discrete geometry through careful visualization. Visualization is fundamental to the theory and practice of geometry, and many arguments or explanations are simpler, or indeed redundant, in a visual medium.
Prerequisites #
The perspective I advocate is cross-disciplinary, and this makes an "ideal reader" hard to gauge. Instead, I have assumed my reader to be myself at age 17: a curious undergraduate interested in various computer science and pure mathematics fields, but not deeply versed in any, and willing to read other references where necessary.
I use an informal style that attempts to be more engaging, rather than maximizing the information density of the text as is typical of academic writing. Eventually there will be a more terse, academic-style summaries of relevant "chunks" of work as they are completed and worthy of publication outside of this medium.
Format #
This site represents a "living document" of a work in progress, detailing the topics within quiver geometry that I am confident enough to explain and illustrate.
Some pages contain missing subsections marked "under construction" -- these are conceptually complete but require writeup that I haven't got around to yet. Gray sections on the navigation menu on the left represent ideas that are, at best, partially developed, and require future work.
Prior work and references #
Unfortunately, this document doesn't currently have inline references. A full index and bibliography is forthcoming.
The closest existing body of ideas lies in geometric group theory, which roughly speaking uses Cayley graphs of groups as way to view groups as geometric objects. In a different direction, discrete differential geometry aims to discrete continuous manifolds for use in computational geometry. Lastly, topological crystallography studies graphs associated with crystallographic lattices.
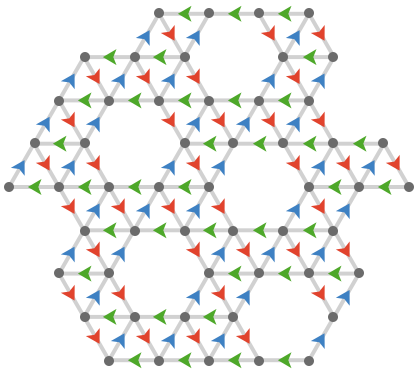
Physics #
While quiver geometry doesn’t make immediate connections to physics, it does aim to populate the toolbox of ideas and methods we might use to build and analyze models of fundamental physics that are discrete, finite, and computable, such as that proposed by e.g. the Wolfram Physics Project, Gerard t'Hooft, and others.
If the universe does turn out to be operating on fundamentally discrete, computational principles, we will in retrospect see continuous geometry as an enticing and useful illusion, but one that never had the physical basis that was its historical justification and inspiration.
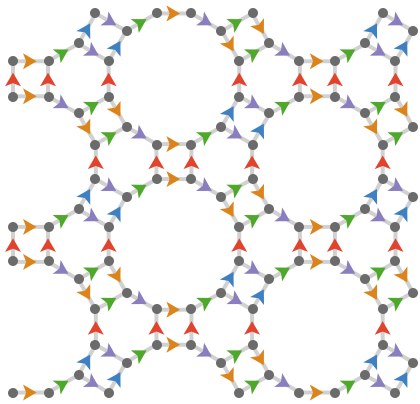
The continuum #
From a philosophical point of view, I believe we should attempt to construct continuous geometries as the limiting cases of particular discrete geometries. I'm not yet certain how to accomplish this. But I believe it will yield more insight than trying to construct discrete geometries by "discretizing" continuous geometries, by forcing us to embrace combinatorial and computational approaches from the very beginning.