Rewriting of field configurations #
Fiber bundles #
A discrete fiber bundle is a total graph \( \totalSpaceStyle{\quiver{E}} \) that is locally a product of a base graph \( \baseSpaceStyle{\quiver{B}} \) and a fiber \( \fiberSpaceStyle{\quiver{F}} \). Here we take \( \baseSpaceStyle{\quiver{B}} = \bindCardSize{\subSize{\lineQuiver }{8}}{\card{\daBlFo{b}}} \) and \( \fiberSpaceStyle{\quiver{F}} = \bindCardSize{\subSize{\lineQuiver }{3}}{\card{\daReFo{f}}} \):
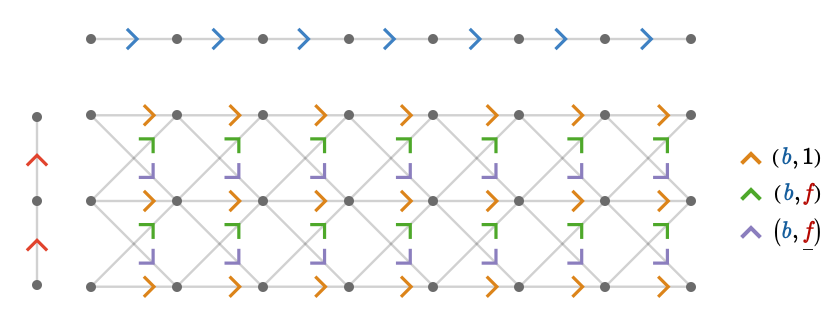
1-paths in the total space are parallel combinations of 1-paths in the base space and 0- and 1-paths in the fiber.
The projection map \( \bundleProjectionStyle{\pathHomomorphism{ \pi }} \) maps a path in the total quiver to the path in the base quiver that consists only of the first factor vertex of each product vertex, and whose cardinals consist of the first factor cardinal of each product cardinal. In other words, the cardinals are mapped as follows:
\[ \assocArray{\mto{\cardinalProduct{\card{\daBlFo{b}},\inverted{\card{\daReFo{f}}}}}{\card{\daBlFo{b}}},\mto{\cardinalProduct{\card{\daBlFo{b}},1}}{\card{\daBlFo{b}}},\mto{\cardinalProduct{\card{\daBlFo{b}},\card{\daReFo{f}}}}{\card{\daBlFo{b}}}} \]Below we visualize the "graph" of a section of this quiver bundle:
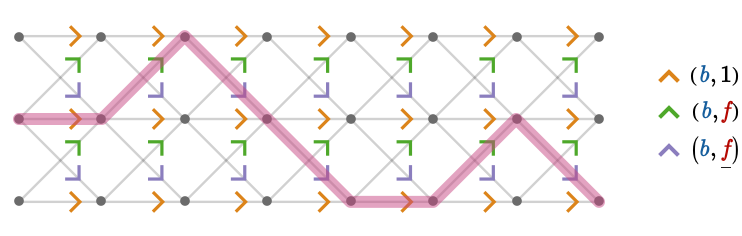
The corresponding section \( \functionSignature{\function{\bundleSectionStyle{\pathHomomorphism{ \sigma }}}}{\baseSpaceStyle{\quiver{B}}}{\totalSpaceStyle{\quiver{E}}} \) is then a path homomorphism that sends a path in the base quiver \( \baseSpaceStyle{\quiver{B}} \) to the corresponding "lifted" path that is a connected component of the fragment of the sub-graph illustrated above. For example, we show the image of two such paths in the base quiver:
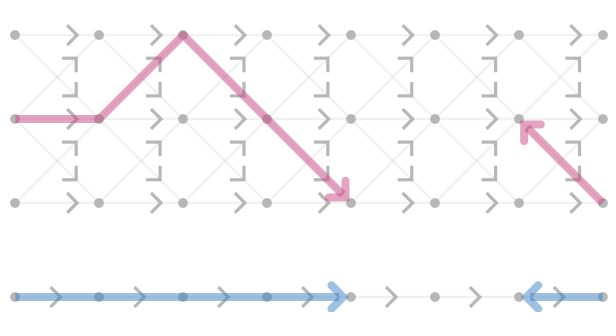
We interpret these sections as field configurations.
Rewriting of sections #
We specify that field configurations will be rewritten such that they remain valid sections:
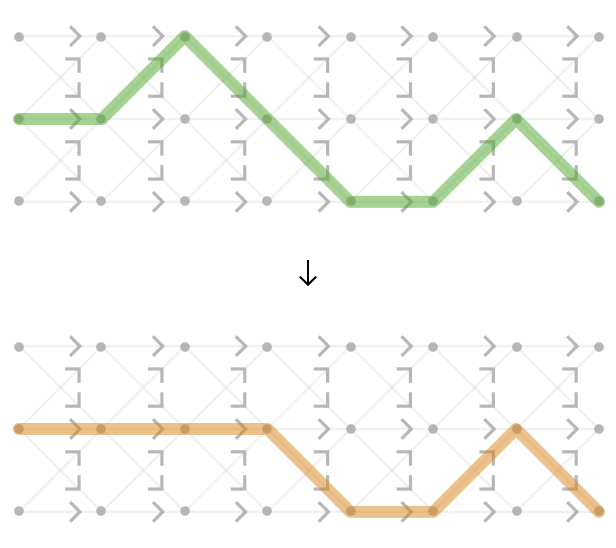
These can be expressed as graph rewrite rules that involve both "static" edges representing the local structure of \( \baseSpaceStyle{\quiver{B}} \) and \( \fiberSpaceStyle{\quiver{F}} \), and "dynamic" edges that represent portions of the section \( \bundleSectionStyle{\pathHomomorphism{ \sigma }} \).