Graph automomorphisms #
Cayley quiver #
Fix a generating set \( \setSymbol{C} = \SeFo{\groupGenerator{c_{\sym{i}}}} \) of a group \( \group{G} \). The vertices of the Cayley quiver \( \cayleyQuiverSymbol{\setSymbol{C}} \) are elements \( \elemOf{\groupElement{g}}{\group{G}} \), and the labeled edges \( \tde{\groupElement{g}}{\groupElement{h}}{\groupGenerator{c_{\sym{i}}}} \) are present when \( \groupElement{h} = \groupGenerator{c_{\sym{i}}}\Gmult \groupElement{g} \).
The natural Cayley quiver for \( \mathbb{Z} \) is the line quiver \( \subSize{\lineQuiver }{ \infty } \):

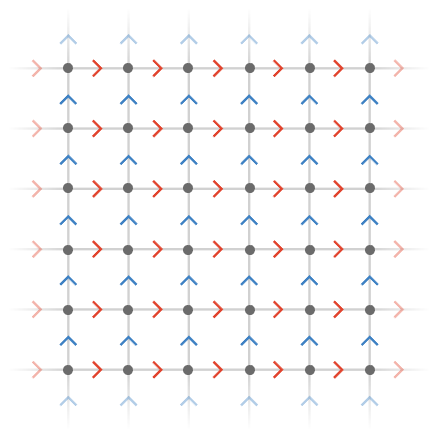
The natural Cayley quiver for \( \mathbb{Z}^2 \) is the square quiver \( \subSize{\squareQuiver }{ \infty } \):
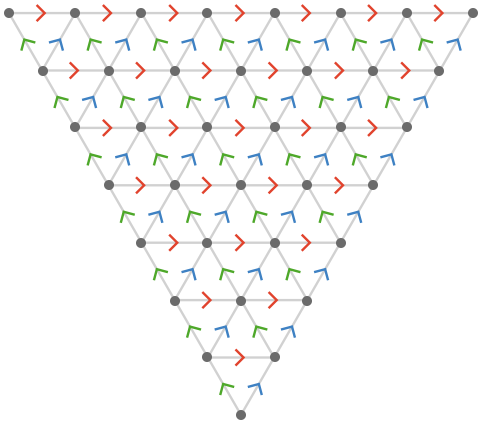
With a different generating set \( \setSymbol{C} = \list{\TuFo{0, 1},\TuFo{1, 0},\TuFo{1, 1}} \), the Cayley quiver \( \cayleyQuiverSymbol{\setSymbol{C}} \) is the triangular quiver \( \subSize{\triangularQuiver }{ \infty } \):
Automorphisms #
An graph homomorpism \( \graphHomomorphism{ \pi } \) is a mapping from edges of a graph \( \graph{G} \) to the edges of a graph \( \graph{H} \) that preserves locality: incident edges of \( \graph{G} \) are mapped to incident edges of \( \graph{H} \).
A graph endomorphism is a mapping from edges of a graph \( \graph{G} \) to themselves.
Invertible graph endomorphisms are called graph automorphsims.
The set of graph automomorphisms of \( \graph{G} \) is written \( \grAuFu(\graph{G}) \), and forms a group in which the group operation is composition of automophisms.
For a choice of generating automomorphisms, \( \grAuFu(\graph{G}) \) yields a Cayley quiver, in which vertices represent automorphisms and edges represent the action of the generating automorphisms on these.
Examples #
For a finite line graph \( \subSize{\lineQuiver }{\sym{n}} \), the automorphism group is isomorphic to \( \cyclicGroup{2} \), consisting of the identity and the reversal homomorphism. There are no translation automorphisms because of "edge effects" -- the end vertices are the only vertices of degree 1, and hence must be sent to themselves (giving the identity automorphism) or eachother (giving the reversal automorphism).
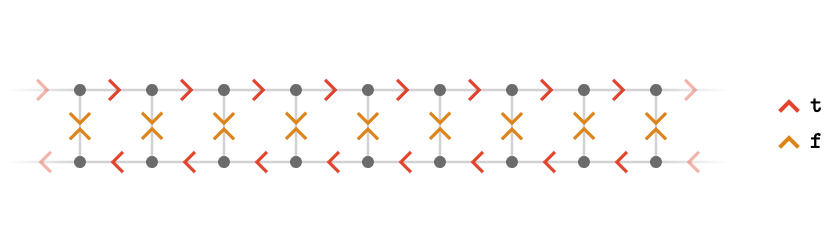
For the infinite line graph \( \subSize{\lineQuiver }{ \infty } \), the automorphism group is \( \maTeFo{Dih}_ \infty \), the infinite dihedral group, consisting of translations \( \sym{n} \) along the line, combined with reversals. Choosing the generating set \( \setSymbol{C} = \list{\reFo{\card{t}},\orFo{\card{f}}} \), where \( \reFo{\card{t}} \) is translation forward by one vertex and \( \orFo{\card{f}} \) is reflection in a fixed origin vertex, we obtain the Cayley quiver \( \cayleyQuiverSymbol{\setSymbol{C}} \):
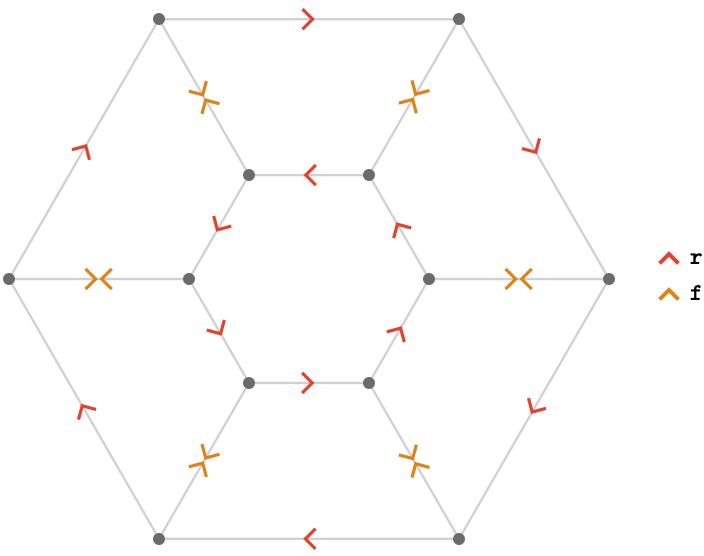
For the finite cycle graph \( \subSize{\cycleQuiver }{\sym{n}} \), the automorphism group is \( \maTeFo{Dih}_{\sym{n}} \), one of the finite dihedral groups, consisting of translations modulo \( \sym{n} \) ("rotations"), combined with reversals. If we choose \( \setSymbol{C} = \list{\reFo{\card{r}},\orFo{\card{f}}} \), where \( \reFo{\card{r}} \) is translation clockwise by one vertex and \( \orFo{\card{f}} \) is reflection in a fixed origin vertex, we obtain the Cayley quiver \( \cayleyQuiverSymbol{\setSymbol{C}} \):