Closed forms for string rewriting systems #
Project description #
The goal of the project is to look at all of the 1-1 and 2-2 string rewriting systems on two characters, and understand their behavior enough to find "closed forms" for their multiway quivers. The linear and circular string rewriting versions of these rules will be compared. Time permiting we will apply some group theory to express their symmetries.
Length 1: #
Trivial:
Conversion:
Length 2: #
Trivial:
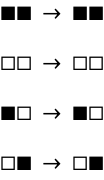
Conversion:
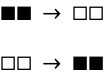
Sorting:
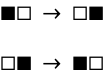
Gobbling:
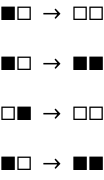
Inverse gobbling:
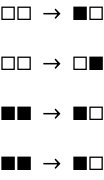
Current progress #
Trivial rules #
Trivial rules can be ignored, as they only introduce self-loops in the multiway quiver, even when combined with other rules into a compound-rule rewriting system.
Length 1 conversions #
Linear case #
1-1 conversion rules simply convert characters of one form to another. For a conversion rule of the form \( \rewrite{\lchar{\texttt{■}}}{\lchar{\texttt{□}}} \) the multiway quiver is a \( \sym{k} \)-dimensional hypercube, where \( \sym{k} \) is the number of \( \lchar{\texttt{■}} \) characters in the intitial condition. This multiway quiver is formally given by:
\[ \bindCardSize{\gridQuiver{\sym{k}}}{\underRepeated{2,\elSy,2}{\sym{k}}}\isomorphicSymbol \underRepeated{\subSize{\lineQuiver }{2}\cartesianProductSymbol \elSy\cartesianProductSymbol \subSize{\lineQuiver }{2}}{\sym{k}} \]This occurs because the rewrites of individual \( \lchar{\texttt{■}} \) characters in the initial condition are independent, and each rewrite yields an single edge of a line quiver.
Sorting rules #

Linear case #
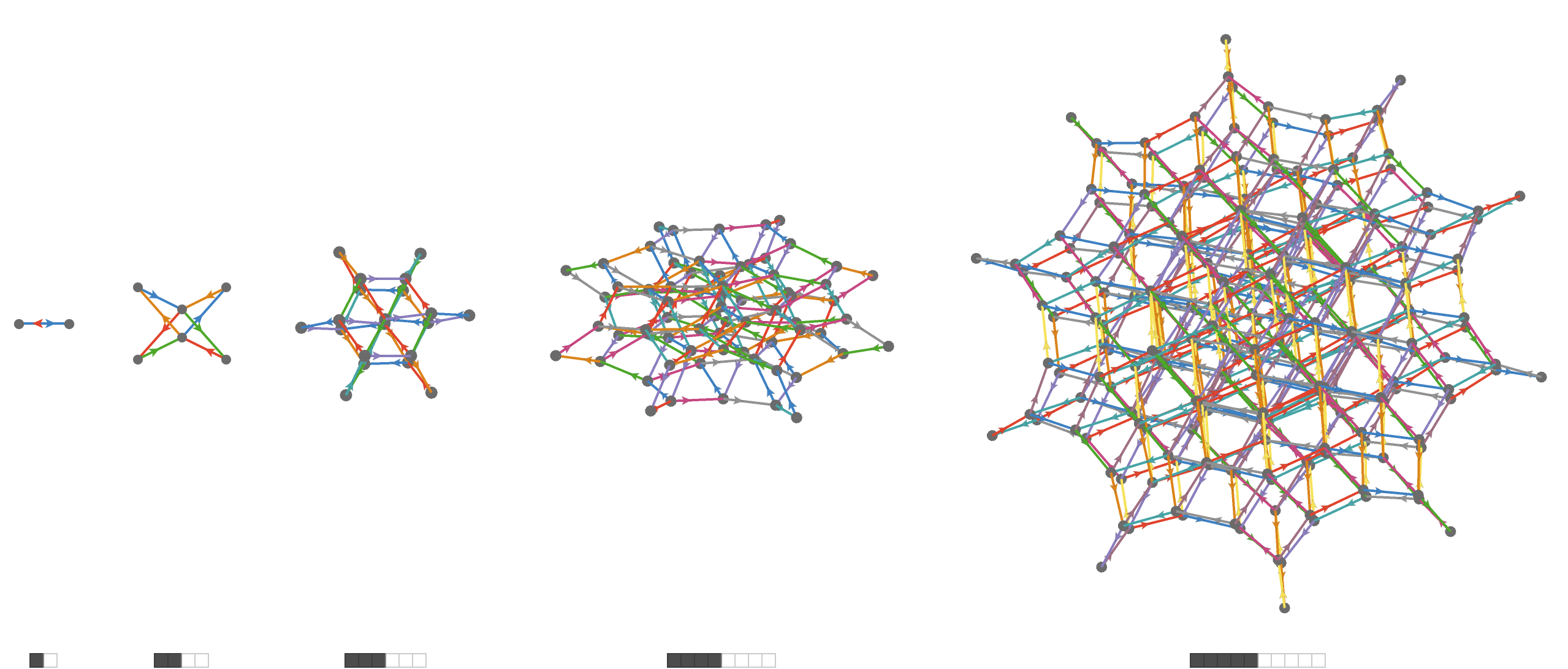
For a maximally unsorted string, we have initally only one rewrite, followed by succesively more possible rewrites that are counted by Binomial.
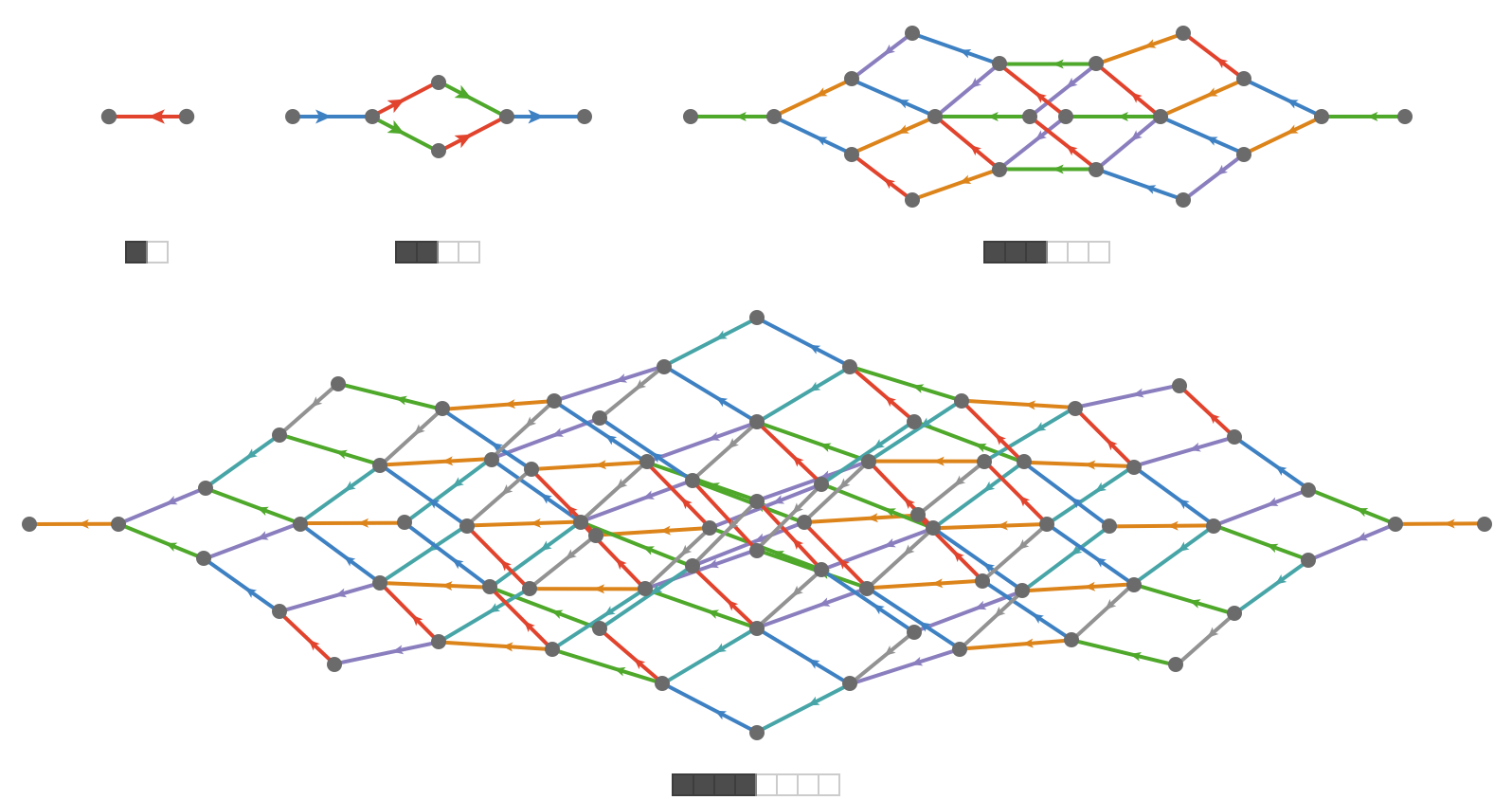
These resemble "cube complexes" that occur in geometric group theory, a connection that might be made more precise.
Additionally, we have some interesting special cases. With all but one cell being black or white, we obtain simple "gliders":
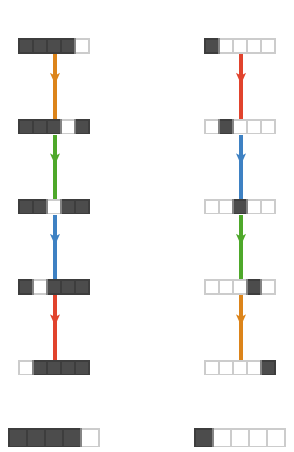
Two initial:
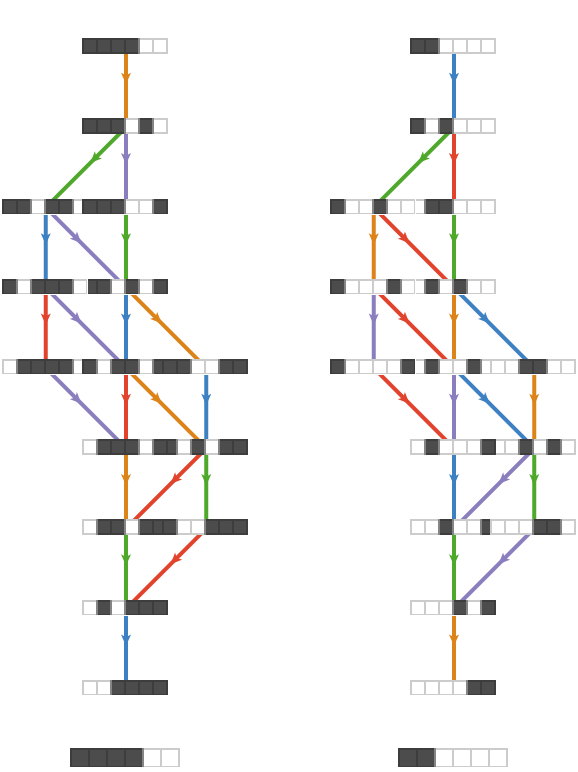
Circular case #
Much additional symmetry is visible when we move to the circular setting.
Again, the special cases are interesting: