Graphs and paths #
This is an example of a basic graph:
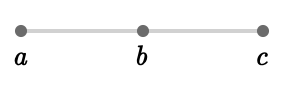
We've labeled the vertices \( \gdef\ChEmGrPaFo#1{#1^●} \gdef\EmGrPaFo#1{#1:#1} \gdef\LaCoPlSq#1{\textcolor{#1}{\raisebox{-0.1em}{\;▢\;}}} \gdef\fiPlSq{\raisebox{-0.05em}{\mkern{2pt}▧}} \vert{a},\vert{b},\vert{c} \).
Basic graphs do not have any notion of direction on their edges, and do not have more than one edge between any two vertices.
We write the edges explicitly as \( \ue{\vert{a}}{\vert{b}} \) etc. We can also refer to them symbolically as \( \edge{e},\edge{f} \), etc.
Because edges are undirected, \( \ue{\vert{a}}{\vert{b}}\syntaxEqualSymbol \ue{\vert{b}}{\vert{a}} \)
A path on a basic graph is an alternating sequence of vertices and edges, beginning and ending with a vertex, such that each edge matches the neighboring two vertices:
\[ \vert{a}:\ue{\vert{a}}{\vert{b}}:\vert{b}:\ue{\vert{b}}{\vert{c}}:\edge{c}:\elSy:\edge{z} \]Using symbols for the edges, we can write this as:
\[ \vert{a}:\edge{e}:\edge{f}:\elSy:\edge{z} \]Alternatively we can write this more compactly by chaining together several edges, where we use arrow-like notation:
\[ \vert{a} \desym \vert{b} \desym \vert{c} \desym \elSy \desym \vert{z} \]While edges in a basic graph are not oriented, paths necessarily are, since they choose a source vertex and a target vertex, and connect them with edges. Hence chained notation uses an arrow-like form, since we can make two distinct paths out of a single edge:
\[ \begin{aligned} \vert{a} \desym \vert{b}&\neq \vert{b} \desym \vert{a}\\ \ue{\vert{a}}{\vert{b}}&= \ue{\vert{b}}{\vert{a}}\end{aligned} \]A path containing no edges must have equal source and target vertices, and so while we can write it fully as \( \EmGrPaFo{\vert{a}} \), we also can use the more compact notation \( \ChEmGrPaFo{\vert{a}} \)
Notation #
A \( \sym{n} \)-path is a path in which \( \sym{n} \) edges appear.
A 0-path is also called an empty path.
Reversal #
We can invert a path by reversing the alternating sequence.
Examples #
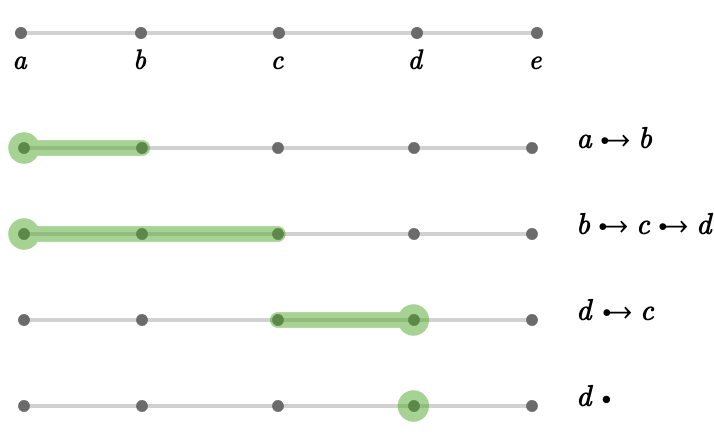
Chaining #
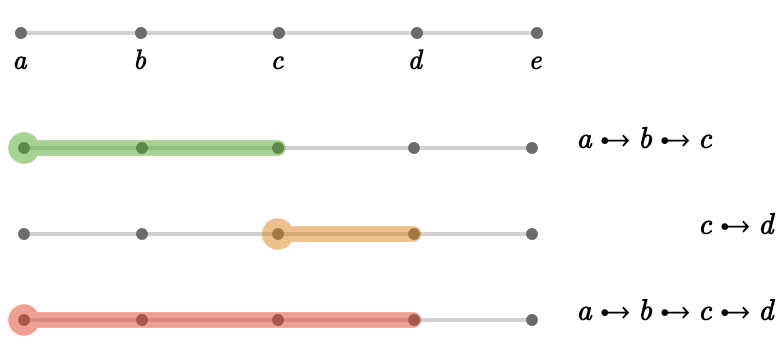
Chaining of paths #
We two paths are target-to-source, we can chain them together into a single path. We write this:
\[ \pathCompose{\paren{\vert{a} \desym \vert{b} \desym \vert{c}}}{\paren{\vert{c} \desym \vert{d}}} = \vert{a} \desym \vert{b} \desym \vert{c} \desym \vert{d} \]Cancellation of paths #
We can adopt the perspective that \( \vert{a} \desym \vert{b} \desym \vert{a} = \ChEmGrPaFo{\vert{a}} \), in other words that a backtracked pair can be removed from any path without changing its value:
\[ \PaFo{\PaFo{\reFo{\fiPlSq{}} \desym \vert{a} \desym \vert{b} \desym \vert{a} \desym \blFo{\fiPlSq{}}}}\syntaxEqualSymbol \boFo{\PaFo{\PaFo{\reFo{\fiPlSq{}} \desym \blFo{\fiPlSq{}}}}} \]We illustrate this here on an example:


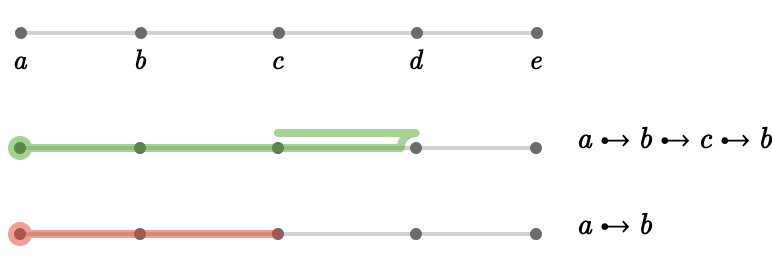
Path groupoid #
Chaining of paths in a graph \( \graph{G} \) forms the operation of a groupoid, the path monoid. When we adopt the perspective of path cancellation, then chaining of paths forms a groupoid, the path groupoid \( \pathGroupoid{\quiver{G}} \).
Ok google!